《hall 定理》小记
算是填一下以前的坑吧。
\(Hall\) 定理
一个关于二分图完美匹配的定理。
设两边的点集为 \(|X|,|Y|\) ,当匹配数达到 \(min(|X|,|Y|)\) 的时候,我们称之为有完美匹配。
钦定 \(|X|\le|Y|\)
定理:
当我们从 \(|X|\) 集合中任意选择一个点集 \(|S|\) ,然后把点集 \(|S|\) 连着的 \(|Y|\) 中的点,记为 \(N(S)\) ,也就是邻域。当满足对于任意 \(S\) ,都有 \(|S|\le N(S)\) 那么这个图就存在完美匹配。
证明:
首先如果存在完美匹配,显然对于所有 \(S\) ,都有 \(|S|\le N(S)\)
但是对于充分性的话,我们考虑反证法,设存在这个条件,但没有完美匹配。
而如果对于任意 \(S\) 都满足 \(S\le N(S)\) ,那么也就是说此时,如果 \(S\) 中有一个点 \(a\) 没有匹配到,那么他可以选择一个与他连接的点进行匹配,记为 \(b\) 。
如果 \(b\) 没被匹配过,那就只就匹配。如果已经被匹配过了,那么就把与 \(b\) 匹配的点加入 \(|S|\) 中,加入后,我们能保证右侧至少有一个点是我们之前没有尝试选择过的,否则就不满足我们的前提条件。让这个与 \(b\) 匹配的点去匹配另一个与他相连的点。
就这样我们不断从 \(|X|\) 中加入新的点进 \(|S|\) 但是因为 \(|X|\) 是有限的,所以最终一定能够匹配成功,所以命题矛盾,原命题成立。
推论:
一个二分图的最大匹配 \(=|X|-max(|S|-|N(S)|)\)
上面的式子可以变成 \(min(|X|-|S|+|N(S)|)\)
至于如何证明,我们可以用二分图来建立网络流模型,将 \(|X|-|S|\) 看成左边割掉的点,将 \(|N(S)|\) 看做右边割掉的点,那么取一个 \(min\) 就是最小割。
那么最小割等于最大流等于最大匹配,得证。
不过我们还可以感性理解,就是说找到一个 \(|S|-N(S)\) 差值最大的集合,减去显然就是我们最多能匹配到的点数。
来几道例题:
P3488 [POI2009] LYZ-Ice Skates
显然我们可以建立二分图模型跑网络流,但是会爆炸,考虑到题目问我们有没有完美匹配。
可以使用 \(hall\) 定理快速判断。
假设我们选择一个 \(l\sim r\) 中的人,作为我们的 \(|S|\)
那么当满足
\(\sum\limits_{i=l}^rnum_i>(r+d-l+1)\times k=\sum\limits_{i=l}^rnum_i>(r-l+1)\times k+d\times k=\sum\limits_{i=l}^R(num_i-k)>d\times k\)
右边是一个常数我们要是左边尽可能大,维护最大子段和咨客。
时间复杂度 \(O(n\log m)\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=5e5+10;
LL n,m,k,d;
struct daduoli {
LL s,ls,rs,d;
}tr[MAXN*4];
void psup(int u) {
int l=(u<<1),r=(u<<1|1);
tr[u].s=tr[l].s+tr[r].s;
tr[u].ls=max(tr[l].ls,tr[l].s+tr[r].ls);
tr[u].rs=max(tr[r].rs,tr[r].s+tr[l].rs);
tr[u].d=max(max(tr[l].d,tr[r].d),tr[l].rs+tr[r].ls);
}
void update(int u,int l,int r,int x,LL y) {
if(l>x||r<x) return ;
if(l==r) {
tr[u].s+=y;
tr[u].ls+=y;
tr[u].rs+=y;
tr[u].d+=y;
return ;
}
int mid=(l+r)/2;
update((u<<1),l,mid,x,y);
update((u<<1|1),mid+1,r,x,y);
psup(u);
}
int main () {
scanf("%lld%lld%lld%lld",&n,&m,&k,&d);
for(int i=1;i<=n;++i) {
update(1,1,n,i,-k);
}
for(int i=1;i<=m;++i) {
LL x,y;
scanf("%lld%lld",&x,&y);
update(1,1,n,x,y);
if(tr[1].d>(LL)k*d) puts("NIE");
else puts("TAK");
}
return 0;
}
Round Marriage
显然考虑二分答案。
我们设 \(nl_i\) 表示 \(i\) 能配对的最左边的新娘是谁(可以走过环), \(nr_i\) 表示 \(i\) 能配对的最右边的新娘是谁。
然后我们显然可以破环成链。
不过对于每次我们都跑一次二分图显然要寄。
我们考虑假设我们选择了连续一段 \(l\sim r\) 的新郎,因为肯定是连续一段的新郎才能使得能配对的新娘尽可能的少。
\(r-l+1>nr_r-nr_l+1\)
当满足上面这个条件时,不成立。移一下项有
\(nl_l-l>nr_r-r\)
我们维护前缀最大的 \(nl_l-l\) 即可。
将 \(a,b\) 都复制四份貌似很好操作。
时间复杂度 \(O(n\log n)\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=2e5+10;
LL n,L;
LL a[MAXN*4],b[MAXN*4],nl[MAXN*4],nr[MAXN*4];
bool check(LL k) {
int l=1,r=0;
for(int i=1;i<=n*3;++i) {
while(r<n*4&&a[i]+k>=b[r+1]) ++r;
while(l<=r&&a[i]-b[l]>k) ++l;
nl[i]=l; nr[i]=r;
}
LL da=-1e18;
for(int i=n+1;i<=n*3;++i) {
da=max(da,nl[i]-i);
if(nr[i]-i<da) return false;
}
return true;
}
LL erfind() {
int l=-1,r=L+1,mid;
while(l+1<r) {
mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid;
}
return r;
}
int main () {
scanf("%lld%lld",&n,&L);
for(int i=1;i<=n;++i) {
scanf("%lld",&a[i]);
}
for(int i=1;i<=n;++i) {
scanf("%lld",&b[i]);
}
sort(a+1,a+1+n);
sort(b+1,b+1+n);
for(int i=1;i<=n*3;++i) a[i+n]=a[i]+L;
for(int i=1;i<=n*3;++i) b[i+n]=b[i]+L;
printf("%lld\n",erfind());
return 0;
}
Allowed Letters
考虑试填法,然后跑 \(hall\) 定理即可。
时间复杂度 \(O(n2^{\sum})\) 貌似有一个 \(\sum^2\) 的常数。
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=2e5+10;
char ch[MAXN],ch1[MAXN],ans[MAXN];
int n,m,num[MAXN],lim[(1<<6)],p[6];
void add(int i,int val) {
for(int j=1;j<(1<<6);++j) {
if((num[i]&j)==num[i]) {
lim[j]+=val;
}
}
}
bool check() {
for(int j=0;j<(1<<6);++j) {
int ans=0;
for(int q=0;q<6;++q) {
if(!((j>>q)&1)) continue;
ans+=p[q];
}
if(ans<lim[j]) return false;
}
return true;
}
int main () {
scanf("%s",ch+1);
n=strlen(ch+1);
for(int i=1;i<=n;++i) {
++p[ch[i]-'a'];
}
scanf("%d",&m);
for(int i=1;i<=m;++i) {
int opt;
scanf("%d",&opt);
scanf("%s",ch1+1);
int ls=strlen(ch1+1);
for(int j=1;j<=ls;++j) {
num[opt]|=(1<<(ch1[j]-'a'));
}
}
for(int i=1;i<=n;++i) {
if(!num[i]) num[i]=(1<<6)-1;
add(i,1);
}
for(int i=1;i<=n;++i) {
bool sf=0;
for(int j=0;j<6;++j) {
if(!num[i]||(num[i]&(1<<j))==(1<<j)) {
if(!p[j]) continue;
--p[j]; add(i,-1);
if(check()) {
sf=1;
ans[i]=char(j+'a');
break;
}
++p[j]; add(i,1);
}
}
if(!sf) {
puts("Impossible");
return 0;
}
}
for(int i=1;i<=n;++i) cout<<ans[i];
puts("");
return 0;
}
[ARC106E] Medals
好题。
首先肯定是呀二分答案的。
但是这里我们需要一个很重要的性质,答案在 \(2kn\) 以内。
因为一个人至多用 \(2k\) 那么 \(n\) 个人至多用 \(2kn\)
虽然看上去有一点不太合理,但是他是对的,至于证明我也不会,大概证明分讨一下应该就好了。
反正我们有了这个性质之后就可以做了。
我们要求是否满足有 \(|S|>|N(S)|\)
看到 \(n\) 很小,显然可以考虑状压来求。
但是我们如何求 \(|N(S)|\) 呢,显然如果要求 \((|N(S)|)\) 他的条件是 \(|\) 不好处理,考虑转换成 \(\&\) ,我们可以用 \(mid\) 减去不在邻域里面的数就可以算出,而怎么算这玩意呢,状压枚举子集要 \(O(3^n)\) 显然不行,可以使用高位前缀和,虽然还不会,不过抄就完了,时间复杂度 \(O(2kn+2^nn\log(2kn))\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=20,NN=3600010;
LL n,m,k;
LL a[MAXN],st[NN],f[(1<<18)],S;
bool check(LL mid) {
for(int i=0;i<S;++i) f[i]=0;
for(int i=1;i<=mid;++i) ++f[st[i]];
for(int i=0;i<n;++i) {
for(int j=0;j<S;++j) {
if(!((j>>i)&1)) f[j|(1<<i)]+=f[j];
}
}
for(int i=0;i<S;++i) {
int cnt=0;
for(int j=0;j<n;++j) {
if((i>>j)&1) ++cnt;
}
if(mid-f[S-1-i]<cnt*k) return false;
}
return true;
}
LL erfind() {
LL l=0,r=(LL)m+1,mid;
while(l+1<r) {
mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid;
}
return r;
}
int main () {
scanf("%lld%lld",&n,&k); m=2*n*k; S=(1<<n);
for(int i=1;i<=n;++i) {
scanf("%lld",&a[i]);
}
for(int i=1;i<=m;++i) {
for(int j=1;j<=n;++j) {
int t=(i-1)%(a[j]*2)+1;
if(t<=a[j]) st[i]|=(1<<(j-1));
}
}
printf("%lld\n",erfind());
return 0;
}
[ARC076F] Exhausted?
首先显然按照一维排序,然后我们从小到大枚举,钦定第 \(i\) 个必选,这时候考虑右端点的影响。
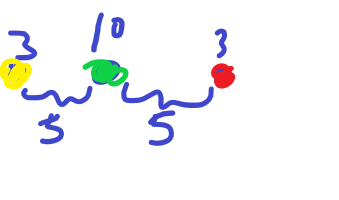
首先加入最右边红色的这个点可以选,那么我们看一下绿色这个点可不可以选,如果选了绿色的点,我们会多五把椅子可以做,但是我们会多 \(10\) 个人,这显然是赚的可以选,而对于黄色的点,如果选了,多三个人,但是会多 \(5\) 把椅子显然是亏的。
所以我们就要找到一段右边连续的值,使得人减椅子数最大。
这个东西可以用线段树维护,每次加入一个右端点为 \(r_i\) 的人,就把 \(0\sim r_i\) 都加一,表示如果选了他们这之中的一个数,人与椅子的差值加一,所以其实线段树维护的就是一个后缀人减椅子数。
然后根据我们 \(hall\) 定理的推论,可以知道最大匹配数 \(=|X|-max(|S|-|N(S)|)\) 然后根据这个算一下,就可以知道要加多少把椅子了。
不过有一个要注意的点,就是说当 \(l,r\) 重叠的时候,我们是视作减去他们之中重叠的椅子,最后再减去,具体看代码实现。
时间复杂度 \(O(nlogn)\)
点击查看代码
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=2e5+10;
int n,m;
struct daduoli {
int l,r;
}a[MAXN];
int tr[MAXN*4],lb[MAXN*4];
void psup(int node) {
tr[node]=max(tr[(node<<1)],tr[(node<<1|1)]);
}
void build_tree(int node,int l,int r) {
if(l==r) {
if(l!=0) tr[node]=-(m-l+1);
else tr[node]=-m;
return ;
}
int mid=(l+r)/2;
build_tree((node<<1),l,mid);
build_tree((node<<1|1),mid+1,r);
psup(node);
}
bool cmp(daduoli a,daduoli b) {
if(a.l!=b.l) return a.l<b.l;
return a.r>b.r;
}
void zx(int node,int x) {
lb[node]+=x;
tr[node]+=x;
}
void psdn(int node) {
if(lb[node]) {
int ls=(node<<1),rs=(node<<1|1);
zx(ls,lb[node]);
zx(rs,lb[node]);
lb[node]=0;
}
}
void update(int node,int l,int r,int x,int y) {
if(l>y||r<x) return ;
if(l>=x&&r<=y) {
// if(l==0) cout<<tr[node]<<' ';
zx(node,1);
// if(l==0) cout<<tr[node]<<" ";
return ;
}
int mid=(l+r)/2;
psdn(node);
update((node<<1),l,mid,x,y);
update((node<<1|1),mid+1,r,x,y);
psup(node);
}
int main () {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) {
scanf("%d%d",&a[i].l,&a[i].r);
}
build_tree(1,0,m+1);
sort(a+1,a+1+n,cmp);
int ans=n;
int l=1;
for(int i=1;i<=n;++i) {
for( ; l<=a[i].l;++l) {
update(1,0,m+1,0,l);
}
update(1,0,m+1,0,a[i].r);
ans=min(ans,n-max(0,(tr[1]-a[i].l)));
}
cout<<n-ans;
return 0;
}
/*
10 7
1 8
1 8
1 8
1 8
1 8
1 8
1 8
1 8
1 8
1 8
*/
总结:
对于一些题如果要判断能否构成最大匹配,如果直接跑二分图会超时,可以考虑能否用 \(hall\) 定理判定合法性。
然后往往需要把式子列出来转换一下要求的东西,因为要求对于所有子集这个条件太苛刻了。通常可以用数据结构或者贪心之类的维护。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号