《LGJOJ棋盘（三）》解题报告

棋盘（三）
描述

有一个R行C列的棋盘，棋盘被分成R*C个单元格子。你要在棋盘至少放B个棋子。棋盘的每个单元格最多只能放1个棋子。如果两个单元格有公共边，那么这两个单元格称为相邻格子。相邻的两个格子不能同时都有棋子，即棋子不能相邻。此外，还必须满足：对于任意的一个格子j，与格子j相邻的所有格子所放置的棋子的数量总和不能超过1。问有多少种不同的放置方案。答案模1000000007。

输入 (读取文件: chess.in)

一行，3个整数：R,C,B。RC<=190。0<=B<=RC。

输出 (写入文件: chess.out)

一个整数。

输入样例 1

2 3 1

输出样例 1

8
提示

样例解释
如果放1个棋子，有6种不同的方案。

如果放2个棋子，有2种不同的方案。

放不了更多的棋子了。

所以6+2=8。

\({\color{red} {analysis:}}\)

首先这道题有一个非常坑的地方，对于任意一个格子j，与j相邻的个字所放置的棋子的数量不能超过1，他没有说这个格子不能什么东西都不放，那么就会出现下面一种情况：

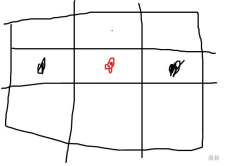
红色是格子j，没有放棋子，而黑色是放了的棋子，所以这是数量为2，与题目相违背，不合法。

那么实际上想放一个棋子

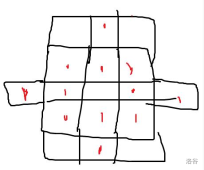
红色的地方都不能有任何棋子。

此时也就是我们放一个棋子就会影响到两列，考虑两列两列处理，即把两列的状态给合并起来。

但这时我们要先把一列中的合法方案给求出来，然后便能将两列两列的状态给处理出来，然后再按两列两列dp即可。

但这题有一些细节，注意：

1、当我们的行数小于列数时，将两个交换一下，实际上对答案并没有影响，但是能保证列数<=14。

2、我们可以先把合法方案给处理出来，这样一定不合法的方案我们就可以省去，减小时间复杂度。

3、题目虽然有190个格子，但至多不会超过65个棋子，为什么自己品。

4、用滚动数组

AC代码：

#include<bits/stdc++.h>

using namespace std;
const int MODD=1000000007;
bool p;
int n,m,k,ans;
int cnt1,hf1[5010],size1[5010],cnt2,hf21[5010],hf22[5010],ttt[5010],size2[5010],dp[2][(1<<14)][65],ppp[5010][5010];
void dfs(int i,int j,int q,int pre1,int pre2)
{
	if(i>m)
	{
		hf1[++cnt1]=j;
		size1[cnt1]=q;
		return ;
	}
	dfs(i+1,j,q,pre2,0);
	if(!pre1&&!pre2)
		dfs(i+1,j|(1<<(i-1)),q+1,0,1);
}
bool check(int i,int j)
{
	if(i&j)return false;
	if((i<<1)&j)return false;
	if(i&(j<<1))return false;
	return true;
}
bool check1(int i,int j)
{
	if(i&j)return false;
	return true;
}
void ycl()
{
	for(int i=1;i<=cnt1;++i)
	{
		for(int j=1;j<=cnt1;++j)
		{
			if(check(hf1[i],hf1[j]))
			{
				hf21[++cnt2]=hf1[i];
				hf22[cnt2]=hf1[j];
				size2[cnt2]=size1[i]+size1[j];
				ttt[cnt2]=j;
				ppp[i][j]=cnt2;
			}
		}
	}
}
void zx()
{
	if(n==1)
	{
		for(int i=1;i<=cnt1;++i)
			if(size1[i]>=k)++ans,ans%=MODD;
		return ;
	}
	for(int i=1;i<=cnt2;++i)dp[p][i][size2[i]]=1;
	for(int i=3;i<=n;++i)
	{
		p^=1;
		memset(dp[p],0,sizeof(dp[p]));
		for(int j=1;j<=cnt2;++j)
		{
			for(int q=1;q<=cnt1;++q)
			{
				if(check1(hf21[j],hf1[q])&&check(hf22[j],hf1[q]))
				{
					int r=size2[j]+size1[q];
					for(int w=64;w>=r;--w)
					{
						dp[p][ppp[ttt[j]][q]][w]+=dp[p^1][j][w-size1[q]];
						dp[p][ppp[ttt[j]][q]][w]%=MODD;
					}
				}
			}
		}
	}
	for(int i=1;i<=cnt2;++i)
		for(int j=k;j<65;++j)
			ans+=dp[p][i][j],ans%=MODD;
}
int main()
{
//	freopen("chess.in","r",stdin);
//	freopen("chess.out","w",stdout);
	cin>>n>>m>>k;
	if(n<m)swap(n,m);
	dfs(1,0,0,0,0);
	ycl();
	zx();
	cout<<ans;
	return 0;
}

总结：

1、状压可以先处理出合法方案，这样可把必定不合法方案去掉，减小常数。

2、滚动数组

3、保证列数小于行数，以节省时间复杂度也是需要掌握的