图的表示

2020年12月9日

搜索一个图是有序地沿着图的边访问所有顶点。

01 图的表示

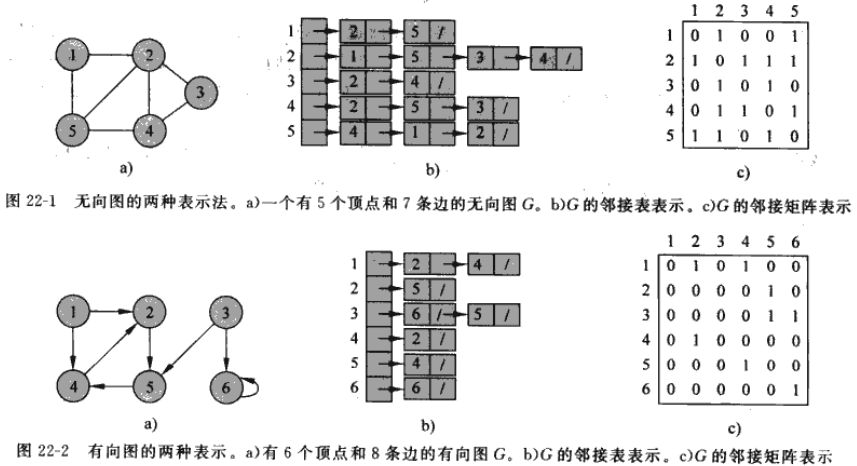
要表示一个图\(G=(V,E)\)，有两种标准的方法，即邻接表和邻接矩阵。这两种表示法既可以用于有向图，也可以用于无向图。

• \(V\)：vertex，顶点
• \(E\)：edge，边

通常采用邻接表表示法，因为用这种方法表示稀疏图（图中\(|E|\)远小于\(|V|^2\)）。当遇到稠密图（图中\(|E|\)接近于\(|V|^2\)）或必须很快判断两个给定顶点是否存在连接边时，通常采用邻接矩阵表示法。

1.1) 邻接表 (adjacency list)表示法

图\(G=(V,E)\)的邻接表表示由一个包含\(|V|\)个列表的数组Adj所组成，其中每个列表对应于\(V\)中的一个顶点。对于每一个\(u \in V\)，邻接表Adj[\(u\)]包含所有满足条件\((u,v) \in E\)的顶点\(v\)。即，Adj[\(u\)]包含图\(G\)中所有和顶点\(u\)相邻的顶点。（或者它也可能包含指向这些顶点的指针。）每个邻接表中的顶点一般以任意顺序存储。

1.2) 邻接矩阵 (adjacency matrix)表示法

在图\(G=(V,E)\)的邻接矩阵表示法中，假定各顶点按某种任意的方式编号为\(1,2,...,|V|\)，那么邻接矩阵为一个\(|V| * |V|\)的矩阵\(A=(a_{ij})\)，它满足：

一个图的邻接矩阵表示需要占用\(O(V^2)\)的存储空间，它与图中的边数多少是无关的。

1.3) 特点

(1) 邻接表表示法

如果\(G\)是一个有向图，则所有邻接表的长度之和为\(|E|\)，这是因为一条形如\((u,v)\)的边是通过让\(v\)出现在Adj[\(u\)]中来表示的。

如果\(G\)是一个无向图，则所有邻接表的长度之和为\(2|E|\)，因为如果\((u,v)\)是一条无向边，那么\(u\)就会出现在\(v\)的邻接表中。

优点：不论是有向图还是无向图，邻接表表示法都有一个很好的特性，即它所需要的存储空间为\(O(V+E)\)。

邻接表稍作改动，即可用来表示加权图，即每条边都有着相应权值的图，权值通常由加权函数\(w: E→R\)给出。例如，设\(G=(V,E)\)是一个加权函数为\(w\)的加权图。对每一条边\((u,v) \in E\)，权值\(w(u,v)\)和顶点\(v\)一起存储在邻接表中。

缺点：如果要确定图中边\((u,v)\)是否存在，只能在顶点\(u\)的邻接表Adj[\(u\)]中搜索\(v\)，除此之外，没有其他更快的方法。这一不足可以通过图的邻接矩阵表示法来弥补，但要以占用更多的存储空间为代价。

(2) 邻接矩阵表示法

优点：可以直接判断两个给定顶点是否存在连接边。

缺点：一个图的邻接矩阵表示需要占用\(O(V^2)\)的存储空间，它与图中的边数多少是无关的。