NP完全性-(Introduction to Algorithms)

2020年12月7日 - 2020年12月9日

01 多项式时间的算法

多项式时间的算法：对规模为n的输入，它们在最坏情况下的运行时间为\(O(n^k)\)，其中k为某个常数。

我们熟悉的时间复杂度有：

\(O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^k) < O(2^n) < O(a^n) < O(n!)\)

把时间复杂度小于\(O(n^k)\)的称为多项式级的复杂度，把时间复杂度大于\(O(n^k)\)的称为非多项式级的复杂度。

02 Overview

NP完全问题：它的状态是未知的，迄今为止，既没有人找出求解NPC问题的多项式时间的算法，也没有人能够证明这类问题不存在多项式时间算法。即所谓的\(P≠NP\)问题。

2.1) P与NPC问题例子

下面列出的两对问题，一个是可以在多项式时间内求解的(P问题)，另一个是NP完全的(NPC问题)，但从表面上来看，两个问题之间的差别很小。

(1) 最短与最长简单路径

最短简单路径：即使在边有负值的情况下，也能在一个有向图\(G=(V,E)\)中，在\(O(VE)\)的时间内，从一个源顶点开始找出最短的路径。

最长简单路径：然而，寻找两个顶点间最长简单路径问题是NP完全的。事实上，即使所有边的权值都是1，它也是NP完全的。

note：一条不具有任何重复顶点的路径被称为简单路径。

(2) 欧拉游程与哈密顿回路

欧拉游程：对一个连通的有向图\(G=(V,E)\)的欧拉游程是一个回路，它遍历图\(G\)中每条边一次，但可能不止一次地访问同一个顶点。可以在\(O(E)\)时间内，确定一个图中是否存在着一个欧拉游程，并且，事实上能够在\(O(E)\)时间内找出这一欧拉游程中的各条边。

哈密顿回路：一个有向图\(G=(V,E)\)的哈密顿回路是一种简单的回路，它包含\(V\)中的每个顶点。确定一个有向图中是否存在哈密顿回路的问题是NP完全的。(确定一个无向图中是否存在哈密顿回路的问题也是NP完全的。)

2.2) P类、NP类、NPC类概述

(1) P类：包含的是在多项式时间内可解的问题。即可以在\(O(n^k)\)时间内求解的问题，此处k是某个常数，n是问题的输入规模。

• The class P consists of those problems that are solvable in polynomial time. More specifically, they are problems that can be solved in time O(n^k) for some constant k, where n is the size of the input to the problem.

(2) NP类：包含的是在多项式时间内“可验证”的问题，此处是指某一解决方案的“证书”，就能够在问题输入规模的多项式时间内，验证该证书是正确的。

• The class NP consists of those problems that are "verifiable" in polynomial time. What we mean here is that if we were somehow given a "certificate" of a solution, then we could verify that the certificate is correct in time polynomial in the size of the input to the problem.

P中的任何问题也都属于NP，这是因为如果某一问题是属于P的，则可以在不给出证书的情况下，在多项式时间内解决它。

现在我们可以暂且相信有\(P \subseteq NP\)，至于P是否是NP的一个真子集，在目前是一个开放的问题。

note：如果A包含于B，且A不等于B，就说集合A是集合B的真子集（proper subset）。

(3) NPC类：从非形式的意义上来说，如果一个问题属于NP，且与NP中的任何问题是一样“难的”(hard)，则说它属于NPC类，也称它为NP完全的(NP-complete)。

• Informally, a problem is in the class NPC-and we refer to it as being NP-complete-if it is in NP and is as "hard" as any problem in NP.

如果任何一个NPC问题可以在多项式时间内解决，则每一个NPC的问题都有一个多项式时间的算法。

多数搞理论研究的计算机科学家认为，NPC问题是难处理的，因为迄今为止研究过的NPC问题非常多，但还没有发现其中任何一个问题的多项式时间解决方案。但是，我们也不能排除NPC问题事实上可以在多项式时间内求解的可能性。

要成为一名优秀的算法设计者，就一定要懂得关于NPC问题的基本原理。如果能确定一个NPC问题，就可以提供充分的论据说明其难处理性。作为一名工程师，更好的做法是花时间开发一种近似算法或解决某种易处理的问题特例，而不是寻找求得问题确切解的一种快速算法。

note：------------------

• P问题 (Polynomial Problem)：可以在多项式时间内解决的问题。
• NP问题 (Non-Deterministic Polynomial Problem)：可以在多项式时间内验证一个解的问题。
• NPC问题 (NP Complete Problem)：所有NP问题都可以在多项式时间内规约(Reducibility)到它并且它本身就是一个NP问题的问题。
• NPH问题 (NP Hard Problem)：所有NP问题都可以在多项式时间内约化(Reducibility)到它，它本身不一定是一个NP问题的问题。

03 证明NPC问题概述

在证明一个问题为NPC问题时，要依赖于三个关键概念：

3.1) 判定问题与最优化问题

• 最优化问题

其中每一种可能的解都有一个相关的值，我们的目标是找出一个具有最佳值的可行解。例如，在最短路径(shortest-path)的问题中，已知的是一个无向图\(G\)及顶点\(u\)和\(v\)，要找出\(u\)到\(v\)之间的经过最少边的路径。(在一个无权、无向图中的单点对间最短路径问题。)

• 判定问题

NPC不直接适合于最优化问题，但适合于判定问题(decision problem)，因为这种问题的答案是简单的“是”或“否”（或者，更为形式地，答案是“1”或“0”）。

note：Decision problem: A problem with the answer of only yes or no.

• 最优化问题转化为判定问题

通常，待优化的值强加一个界，就可以将一个给定的最优化问题转化为一个相关的判定问题。例如，对最短路径(shortest-path)问题来说，它有一个相关的判定问题，就是要判定给定的有向图\(G\)、顶点\(u\)和\(v\)、一个整数\(k\)，在\(u\)和\(v\)之间是否存在一条包含最多\(k\)条边的路径。(这里称之为shortest-path-k问题)

• 最优化问题比判定问题更难

当我们试图证明最优化问题是一个“困难的”问题时，就可以利用该问题与相关的判定问题之间的关系。这是因为，从某种意义来说，判定问题要“更容易一些”，或至少“不会更难”。例如：我们可以先解决shortest-path问题，在将找出的最短路径上边的数目与相关判定问题中参数k进行比较，从而解决shortest-path-k问题。换句话说，如果某个最优化问题比较容易的话，那么其相关的判定问题也会是比较容易的。

按照与NPC更为有关的方式来说：如果我们能够提供表明某个判定问题是个困难问题的话，就等于提供了证据表明其相关的最优化问题也是困难的。

3.2) 归约

我们考虑一个判定问题(称为A)，希望在多项式时间内解决该问题。称某一特定问题的输入为该问题的一个实例 (instance)，例如，shortest-path-k问题的一个实例可以是某一特定的图\(G\)、\(G\)中特定的点\(u\)和\(v\)以及一个特定的整数\(k\)。现在，假设有另一个不同的判定问题(称为B)，我们知道如何在多项式时间内来解决它。最后，假设一个过程，它能将A的任何实例a转换成B的，具有以下特征的某个实例b：

(1) 转换操作需要多项式时间；
(2) 两个实例的答案是相同的。即，a的答案是“是”，当且仅当b的答案也是“是”。

称这样的一种过程为多项式时间的归约算法(reduction algorithm)，并且，它提供了一种在多项式时间内解决问题A的方法。

(1) 给定问题A的一个实例a，利用多项式时间归约算法，将它转换为问题B的一个实例b。
(2) 在实例b上，运行B的多项式时间判定算法。
(3) 将b的答案用作a的答案。

只要上述步骤中的每一步只需多项式时间，则所有三步合起来也只需要多项式时间，这样，我们就有了一种对a进行判断的方法了。

in a word：通过将对问题A的求解“归约”为对问题B的求解，就可以利用B的“易求解性”来证明A的“易求解性”。

NPC是为了反映一个问题有多难，而不是为了反映它是多容易的，因此，我们以相反的方式来利用多项式时间归约，从而说明某一个问题是NPC的。

• 利用归约算法来证明某一特定的问题不存在多项式时间的算法

(1) 假设有一个判定问题A，我们已经知道它不可能存在多项式时间的算法（此时可以先不考虑如何才能找到这样的一个问题A）。进一步假设有一个多项式时间的归约，它将A的一个实例转换为B的实例。
(2) 现在，可以利用反证法来简单地证明B不可能存在多项式时间的算法。先做一个相反的假设，即假设B有一个多项式时间的算法。那么利用归约算法，我们就应该有某种方法能在多项式时间内解决问题A，而这是与A没有多项式时间算法这一假设矛盾的。
(3) 所以B不可能存在多项式时间的算法。

至于NPC，我们不能假设问题A绝对没有多项式时间的算法。然后，证明的方法是类似的，即，假设A是NPC的前提下，来证明问题B是NPC。

3.3) 第一个NPC问题

应用归约技术要有个前提，即已知一个NPC问题，这样才能证明另一个问题也是NPC的。因此，需要找到“第一个”NPC问题。

note：但到现在为止，我们实际上还没有证明任何问题是NPC问题。一旦我们证明了至少有一个问题是NPC问题，就可以用多项式时间可归约性作为工具，来证明其他问题也具有NP完全性。但可以证明存在一个NP完全问题：电路可满足性问题。

04 多项式时间可解的问题（P问题）

接下来形式化的定义：多项式时间可解的问题。

首先必须对问题这一概念进行形式化定义：

4.1) 定义抽象问题

定义抽象问题\(Q\)为在问题实例集合\(I\)和问题解法集合\(S\)上的一个二元关系。

\(Q \subseteq I × S\)

note：Q(Question)、I(Instance)、S(Solution)

eg：shortest-path问题，\(I=\{<G, u, v>\}\)，\(S=\{图中的顶点序列\}\)

4.2) 判定问题

NPC理论关注的是判定问题(decision problem)，即解为“是”或“否”的问题。于是：

抽象的判定问题可看作是从实例集\(I\)映射到解集\(\{0, 1\}\)的一个函数。

eg：shortest-path-k问题，如果对于实例\(i=<G,u,v,k>\)，满足条件：从\(u\)到\(v\)的最短路径的长度至多为\(k\)条边，则\(f(i)=1\)(是)，否则\(f(i)=0\)(否)。

note：如果抽象问题不是判定问题，而是最优化问题，怎么办？将最优化问题转化为判定问题。

4.3) 编码（将抽象问题映射到具体问题上）

如果要用一个计算机程序来求解一个抽象问题，就必须用一种程序能理解的方式来表示问题实例。

抽象对象集合S的编码是从\(S\)到二进制串集合的映射\(e\)。

eg：把自然数\(N=\{0, 1, 2, 3, 4,...\}\)编码为串\(\{0, 1, 10, 11, 100,...\}\)。

note：\(e\)的陪域不一定是二进制串；定义在一个有限字母表(其中至少有两个符号)上的任何串集都是可以的。

因此，“求解”某个抽象判定问题的计算机算法实际上是把一个问题实例的编码作为其输入。

我们把实例集为二进制串的集合的问题称为具体问题。

如果当提供给一个算法的长度为\(n=|i|\)的一个问题实例\(i\)时，算法可以在\(O(T(n))\)时间内产生问题的解，我们就说该算法在时间\(O(T(n))\)内解决了该具体问题。因此，如果对某个常数\(k\)，存在一个算法能在时间\(O(n^k)\)内求解出某具体问题，就说该具体问题是多项式时间可解的。

4.4) 定义复杂类P(complexity class P)

在多项式时间内可解的具体判定问题的集合。

• We can now formally define the complexity class P as the set of concrete decision problems that are polynomial-time solvable.

给定一个抽象判定问题\(Q\)，其映射为实例集合\(I\)到\(\{0,1\}^*\)。

编码：\(e: I→\{0,1\}^*\)，导出\(Q\)相关的具体判定问题。

抽象问题实例\(i \in I\)的解为\(Q(i) \in \{0,1\}\)；
具体问题实例\(e(i) \in \{0,1\}^*\)的解也为\(Q(i) \in \{0,1\}\)。

在技术上，可能存在一些表示无意义的抽象问题实例的二进制串，为了方便起见，假定任何这样的串都映射到0。因此，对表示抽象问题实例的编码的二进制串实例，具体问题与抽象问题产生同样的解。

note：\(\{0,1\}^*\)表示所有由集合\(\{0,1\}\)中的符号构成的串的集合。

4.5) 形式语言体系

从语言理论的观点来看，任何判定问题\(Q\)的实例集，即集合\(∑^*\)，其中\(∑=\{0,1\}\)。因为\(Q\)完全是由那些答案为1(是)的问题实例来描述，因而可以把\(Q\)看作是定义在\(∑=\{0,1\}\)上的一个语言\(L\)，其中：

\(L = \{x\in ∑^* : Q(x)=1 \}\)

note：为什么\(Q(x)=1\)，因为：如果\(Q\)中的答案为0(否)的问题实例是无意义的，比如shortest-path-k问题，是否存在符合条件的最短路径？提供的是一个答案为0(否)的问题实例，只能说明这个实例的情况下是不符合条件的路径，但是并不表明没有符合条件的最短路径。

eg：判定问题shortest-path-k问题对应的语言为：

形式语言体系可以用来表述判定问题与求解这些问题的算法之间的关系。

如果给定输入\(x\)，算法输出\(A(x)=1\)，我们就说算法\(A\)接受串\(x \in \{0,1\}^*\)。如果\(A(x)=0\)，则说算法\(A\)拒绝串\(x\)。

被算法\(A\)接受的语言的集合：\(L=\{x\in\{0,1\}^* : A(x)=1\}\)

即使语言\(L\)被算法\(A\)所接受，该算法也不一定会拒绝一个输入串\(x\)(\(x \notin L\))。例如，算法可能会永远循环下去。

如果\(L\)中的每个二进制串要么被算法\(A\)接受，要么被其拒绝，则说语言\(L\)由算法\(A\)判定。

• 接受、判定

(1)接受：如果对任意长度为\(n\)的串\(x \in L\)和某个常数\(k\)，算法\(A\)在时间\(O(n^k)\)内接受\(x\)，则语言\(L\)在多项式时间内被算法\(A\)接受。

(2)判定：如果对于任意长度为\(n\)的串\(x \in \{0,1\}^*\)和某个常数\(k\)，算法\(A\)可以在时间\(O(n^k)\)内正确的判定\(x \in L\)，则说语言L在多项式时间内被算法\(A\)判定。

因此，要接受一个语言，只需要关心\(L\)中的字符串，但是要判定某一语言，算法必须正确地接受或拒绝\(\{0,1\}^*\)中的每一个串。

4.6) 复杂性类P的形式语言体系的定义

\(P = \{ L \subseteq \{0, 1\}^* : 存在一个算法A能在多项式时间内判定L \}\)

05 多项式时间可验证的问题（NP问题）

对语言进行“验证”的算法。

5.1) 验证算法

把验证算法定义为：含两个自变量的算法\(A\)，其中一个自变量是普通输入串\(x\)，另一个是称为“证书”的二进制串\(y\)。如果存在一个证书\(y\)满足\(A(x,y)=1\)，则该含两个自变量的算法\(A\)验证了输入串\(x\)。由一个验证算法\(A\)所验证的语言是：

\(L = \{x \in {0,1}^* : 存在y\in\{0,1\}^*，满足A(x,y)=1 \}\)

5.2) 复杂类NP

复杂类NP是能被一个多项式时间算法验证的语言类。更准确的地说，一个语言\(L\)属于NP，当且仅当存在一个两输入的多项式时间算法\(A\)和参数\(c\)满足：

\(L = \{x \in {0,1}^* : 存在一个证书y（|y|=O(|x|^c)）满足A(x,y)=1\}\)

我们说算法\(A\)在多项式时间内验证了语言\(L\)。

note：NP，非确定性多项式时间(nondeterministic polynomial time)。

06 NP完全性与可归约性（NPC问题）

NPC问题有一个性质：如果一个NPC问题能在多项式时间内得到解决，那么，NP中的每一个问题都可以在多项式时间内求解，即\(P=NP\)。但是，尽管进行了多年的研究，目前还没有找出关于任何NPC问题的多项式时间的算法。

6.1) 可归约性

一个问题\(Q\)可以被归约为另一个问题\(Q\)，如果\(Q\)的任何实例都可以被“容易地重新描述为”\(Q'\)的实例，而\(Q'\)的实例的解也是\(Q\)的实例的解。

eg：求解关于未知量\(x\)的线性方程问题可以转化为求解二次方程的问题。已知一个实例\(ax+b=0\)，可以把它变换为\(0x^2+ax+b=0\)，其解也是\(ax+b=0\)的解。

因此，如果一个问题\(Q\)可以转化为另一个问题\(Q'\)，则从某种意义上来说，\(Q\)并不比\(Q'\)更难解决。

• 多项式时间归约

语言\(L_1\)在多项式时间内可以归约为语言\(L_2\)，写作\(L_1 ≤ pL_2\)，如果存在一个多项式时间内可计算的函数\(f: \{0,1\}^* → \{0,1\}^*\)，满足对所有的\(x \in \{0,1\}^*\)都有：\(x \in L_1\)当且仅当\(f(x) \in L_2\)；称函数\(f\)为归约函数，计算\(f\)的多项式时间算法\(F\)称为归约算法。

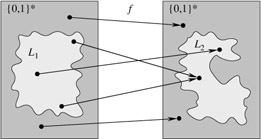
note：\(x \in L_1\)则\(f(x) \in L_2\)，\(x \notin L_1\)则\(f(x) \notin L_2\)

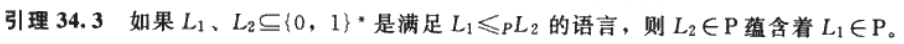
6.2) NP完全性(NPC)

多项式时间归约提供了一种形式方法，用来证明一个问题在一个多项式时间因子内至少与另一个问题一样难。即，如果\(L_1 ≤ pL_2\)，则\(L_1\)大于\(L_2\)的难度不会超过一个多项式时间因子，这就是我们采用“小于等于”来表示归约记号的原因。

• 定义NP完全语言的集合，这些都是NP中最难的问题

6.3) NP完全性是判定P是否等于NP的关键

6.4) P、NP、NPC之间的关系

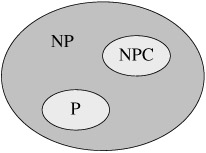
note：大多数理论科学家眼里的P、NP和NPC三者之间的关系。

6.5) P、NP、NPC、NPH之间的关系

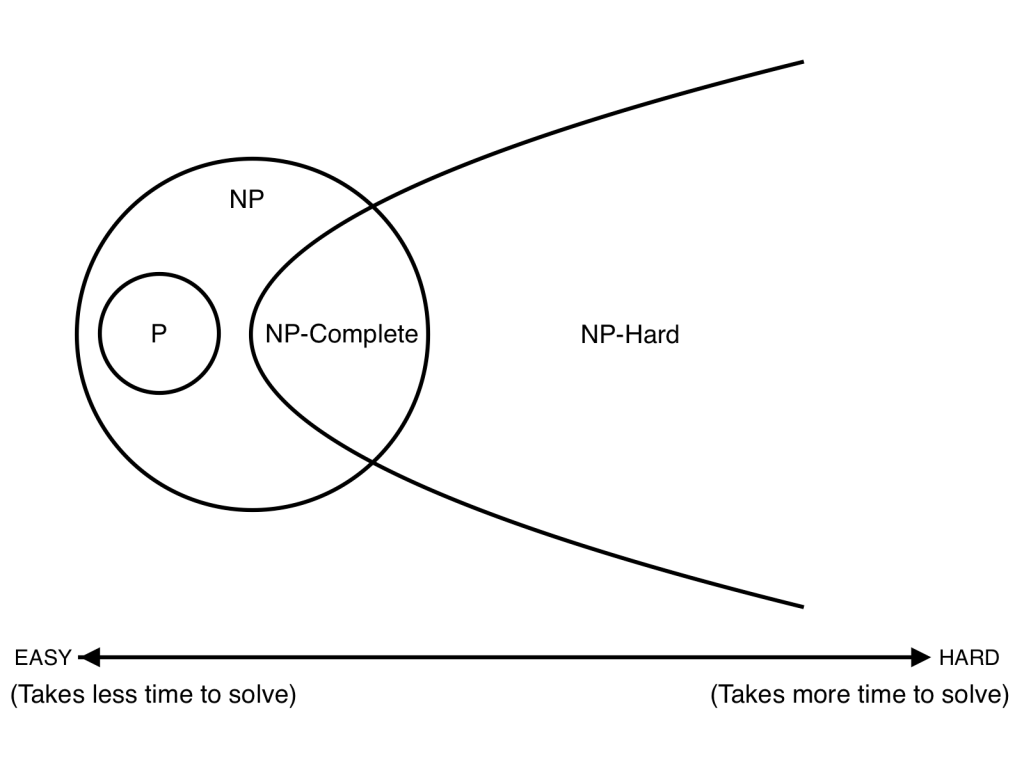
Summary

(1) P (Polynomial time decidable) (Deterministic linear time decidable)

• (If and only if) The set of decision problems that can be decided by a DTM (Deterministic Turing Machine) in polynomial time.
• Can trivially decided by a NTM in polynomial time.
• [Concept] can be decided in polynomial time must can be verified in polynomial time.
• [Example] All sorting algorithms, BFS, DFS, Boyle-Moore string matching algorithm, Kruskal algorithm, Dijkstra algorithm.

(2) NP (Non-deterministic TM decidable in polynomial time.) (Polynomial time verifiable)

• The sets of decision problems that can be decided by a NTM (Non-deterministic Turing Machine) in polynomial time.
• The set of decision problems that can be verified by a DTM in polynomial time; decided by a DTM in exponential time.
• [Example] Sudoku, Graph isomorphism, Integer factorization. (Integer factorisation is in NP. This is the problem that given integers n and m, is there an integer f with 1 < f < m, such that f divides n (f is a small factor of n)?)

(3) NPC

• It’s a NP problem. AND It’s a NPH problem.
• One/All NP/NPC problem can be reduced to it(NPC) in polynomial time.
• [Example] Knapsack, 3-SAT, 3-colorability, Hamiltonian path, Traveling salesman(decision version), Clique.

(4) NPH

• NP Hard problem is at least as hard as NPC.
• It doesn’t have to be a decision problem.
• [Example] Halting problem, Traveling Salesman problem(applied as vehicle routing), Chess.

(5) Others

• L: Problems that can be solved by a DTM in Logarithm time.
• NL: Problems that can be solved by a NTM in Logarithm time.
• Etcetera.

note：https://williamswu.wordpress.com/2016/04/17/algorithm-np-p-nph-npc/

---

note：------------------

陪域(到达域)

到达域(codomain)，或称为陪域、余定义域、上域、目标集(target set)。

在数学领域中，一个函数的到达域指的是至少包含所有此函数的输出值的一个集合。在函数符号f: X→Y中，Y是函数f的到达域。

f的值域是Y的一个子集，若f是一个满射函数(surjective function)，则f的到达域和值域相等，反之则代表有 y$\in$Y不存在于f的值域中，使得方程f(x)=y无解。

https://zh.wikipedia.org/wiki/到达域

note：------------------

定理、引理、命题

定理（英语：Theorem）是经过受逻辑限制的证明为真的陈述。一般来说，在数学中，只有重要或有趣的陈述才叫定理。证明定理是数学的中心活动。一个定理陈述一个给定类的所有（全称）元素一种不变的关系，这些元素可以是无穷多，它们在任何时刻都无区别地成立，而没有一个例外。

引理是数学中为了取得某个更好的结论而作为步骤被证明的命题，其意义并不在于自身被证明，而在于为达成最终目的作出贡献。一个引理可用于证明多个结论。数学中存在很多著名的引理，这些引理可能对很多问题的解决有帮助

猜想是相信为真但未被证明的数学叙述，或者叫做命题，当它经过证明后便是定理。猜想是定理的来源，但并非唯一来源。一个从其他定理引伸出来的数学叙述可以不经过成为猜想的过程，成为定理。

note：------------------

电路可满足性

前面已经定义了NPC问题这一概念，但到现在为止，我们实际上还没有证明任何问题是NPC问题。一旦我们证明了至少有一个问题是NPC问题，就可以用多项式时间可归约性作为工具，来证明其他问题也具有NP完全性。

因此下面着重来证明存在一个NP完全问题：电路可满足性问题。

note：------------------

NP完全问题

(1) 团问题

(2) 顶点覆盖问题

(3) 旅行商问题

(4) 子集和问题

note：------------------

解决NPC问题的思路

(1) 如果实际输入的规模比较小，则直接用指数运行时间的算法来解决问题。

(2) 或许能将一些重要的、多项式时间可解的特殊情况隔离出来。

(3) 仍有可能在多项式时间里找到近似最优解(near-optimal solution)。