排列与组合-(组合数学)

01 排列

1.1 线性排列

note：把对象排成一条线。

用\(P(n,r)\)表示\(n\)元素集合的\(r\)排列的数目，则：

eg：对于集合{a, b, c}，则P(n,r)中的n=3，假设取r=3，则P(3,3)=3×2×1=6，即abc、acb、bac、bca、cab、cba这6种。

1.2 循环排列

note：把对象排成一个圆。

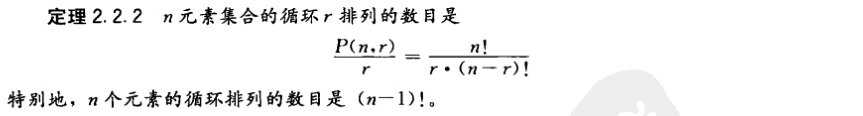
eg：

02 组合

设S是n元素集合。集合S的一个组合通常表示集合S的元素的一个无序选择。这样一个选择的结果是S的元素构成的一个子集(subset)\(A \subseteq S\)。

因此，S的一个组合就是S的子集的一个选择。

我们用\({n \choose r}\)表示n元素集合的r子集的数目。

eg：如果S={a,b,c,d}，那么S的3子集有：{a,b,c}、{a,b,d}、{a,c,d}、{b,c,d}。即，\({4 \choose 3}\)=4。

2.1 常见性质

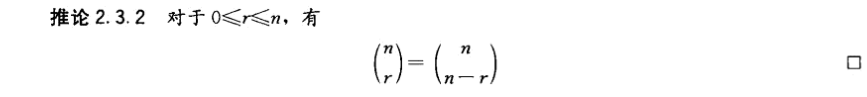
04 多重集合的排列

eg：S={2·a, 1·b, 3·c}就是一个多重集合。

05 多重集合的组合

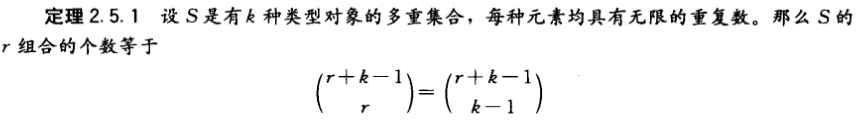
eg：S={2·a, 1·b, 3·c}，S的3组合有：{3·c}、{2·a, 1·b}、{2·a, 1·c}、{1·a, 2·c}、{1·b, 2·c}、{a, b, c}