线性规划

线性规划

概念

线性规划的Matlab标准形式

数学标准型

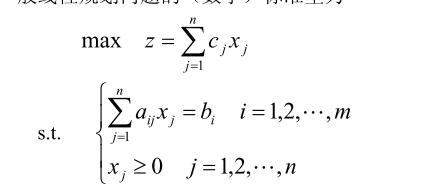
可行解 满足约束条件的解\(x=(x_1,x_2,\cdots,x_n)\)，称为线性规划问题的可行解.
而使目标函数达到最大值的可行解叫最优解。 可行域 所有可行解构成的集合称为问题的可行域，记为R。

解决方法

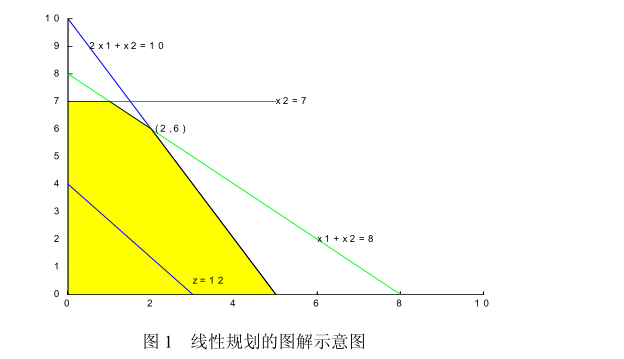
图解法

简单直观，有助于了解线性规划问题求解的基本原理。

Matlab解法

标准公式：

\[\min c^{T} x \]

\[\text { s.t. }\left\{\begin{array}{l} A x \leq b \\ A e q \cdot x=b e q \\ l b \leq x \leq u b \end{array}\right. \]

解决公式

\[[x, \text { fval }]=\operatorname{linprog}\left(\mathrm{c}, \mathrm{A}, \mathrm{b}, \mathrm{Aeq}, \mathrm{beq}, \mathrm{LB}, \mathrm{UB}, \mathrm{X}_{0}, \mathrm{OPTIONS}\right) \]

\(x\)是列向量，这里 fval 返回目标函数的值，LB 和UB分别是变量 x的下界和上界， \(X_0\)是\(x\)的初始值。
OPTIONS 是控制参数。

举例

\[\begin{array}{ll} & \max z=2 x_{1}+3 x_{2}-5 x_{3} \\ \text { s.t. } & x_{1}+x_{2}+x_{3}=7 \\ & 2 x_{1}-5 x_{2}+x_{3} \geq 10 \\ & x_{1}+3 x_{2}+x_{3} \leq 12 \\ & x_{1}, x_{2}, x_{3} \geq 0 \end{array} \]

解决：

c=[2;3;-5];
a=[-2,5,-1;1,3,1]; b=[-10;12]; aeq=[1,1,1]; beq=7;
x=linprog(-c,a,b,aeq,beq,zeros(3,1)) 
value=c'*x

转化为线性规划问题

举例1

\[\begin{aligned} &\min \left|x_{1}\right|+\left|x_{2}\right|+\cdots+\left|x_{n}\right|\\ &\text { S. t. }\\ &A x \leq b \end{aligned} \]

对任意的\(x_i\)存在\(u_i,v_i>0\)满足\(x_{i}=u_{i}-v_{i}, \quad\left|x_{i}\right|=u_{i}+v_{i}\)

\(u_{i}=\frac{x_{i}+\left|x_{i}\right|}{2}, \quad v_{i}=\frac{\left|x_{i}\right|-x_{i}}{2}\)

\(u=\left[\begin{array}{lll}u_{1} & \cdots & u_{n}\end{array}\right]^{T}, \quad v=\left[\begin{array}{lll}v_{1} & \cdots & v_{n}\end{array}\right]^{T}\)

上面的问题就转化为

\[\begin{aligned} &\min \sum_{i=1}^{n}\left(u_{i}+v_{i}\right)\\ &\text { s.t. }\left\{\begin{array}{l} A(u-v) \leq b \\ u, v \geq 0 \end{array}\right. \end{aligned} \]

举例2

\[\min _{x_{i}}\left\{\max _{y_{i}}\left|\varepsilon_{i}\right|\right\} \]

其中\(\varepsilon_{i}=x_{i}-y_{i}\)

取\(x_{0}=\max _{y_{i}}\left|\varepsilon_{i}\right|\)，问题就转换为

\[\begin{aligned} &\min x_{0}\\ &\text { s.t. } \quad x_{1}-y_{1} \leq x_{0}, \cdots, x_{n}-y_{n} \leq x_{0} \end{aligned} \]

举例3

\[\begin{aligned} &\max \quad z=\sum_{j=1}^{n} c_{j}\left|x_{j}\right|\\ &\text { st. }\left\{\begin{array}{l} \sum_{j=1}^{n} a_{i j} x_{j}=b_{i} \quad(i=1,2, \cdots, m) \\ x_{j} \text { 取值无约束 } \end{array}\right. \end{aligned} \]

\(u_{i}=\frac{x_{i}+\left|x_{i}\right|}{2}, \quad v_{i}=\frac{\left|x_{i}\right|-x_{i}}{2}\)

代换即可

[(4条消息) 【MATLAB】线性规划问题中碰到绝对值的情况_Luo199561的博客-CSDN博客