遗传算法详解与实践(单目标)
简介
遗传算法模拟了自然界物竞天择、适者生存的的进化过程,保留好的物种。
遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。
是一种搜索最优解的优化模型,个人感觉很多这种搜索算法都是为了解决局部最优解的问题。遗传算法并不保证你能获得问题的最优解,但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解,而只要简单的“否定”一些表现不好的个体就行了。
理解
遗传算法中每一条染色体/个体,对应着遗传算法的一个解决方案,一般我们用适应性函数(fitness function)来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。
生动理解:
在遗传算法中,有很多袋鼠,它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年,就在一些海拔高度较低的地方射杀一些袋鼠,并希望存活下来的袋鼠是多产的,在它们所处的地方生儿育女。就这样经过许多年,这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上,可是在所有的袋鼠中,只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲(最优解)。
概念
列举
基因型(genotype):性状染色体的内部表现;
表现型(phenotype):染色体决定的性状的外部表现,或者说,根据基因型形成的个体的外部表现;
进化(evolution):种群逐渐适应生存环境,品质不断得到改良。生物的进化是以种群的形式进行的。
适应度(fitness):度量某个物种对于生存环境的适应程度。
选择(selection):以一定的概率从种群中选择若干个个体。一般,选择过程是一种基于适应度的优胜劣汰的过程。
复制(reproduction):细胞分裂时,遗传物质DNA通过复制而转移到新产生的细胞中,新细胞就继承了旧细胞的基因。
交叉(crossover):两个染色体的某一相同位置处DNA被切断,前后两串分别交叉组合形成两个新的染色体。也称基因重组或杂交;
变异(mutation):复制时可能(很小的概率)产生某些复制差错,变异产生新的染色体,表现出新的性状。
编码(coding):DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。
解码(decoding):基因型到表现型的映射。
个体(individual):指染色体带有特征的实体;
种群(population):个体的集合,该集合内个体数称为种群的大小。
编码方式
二进制编码和浮点数编码基因型
人的基因型是46条染色体所描述的却能解码成一个眼,耳,口,鼻等特征各不相同的活生生的人。
编码的前提是了解需要编码的个体的特征,尤其是与问题相关的特征。
物竞天择
物竞体现在适应度函数上。
天择体现在适应度高的个体以较大概率繁殖后代,在种群中产生更多的基因留存。轮盘赌(Roulette Wheel Selection)选择法即是计算适应度函数输入结果占比来确定这个概率。
基因交叉(重组)和变异
重组/交叉
二进制编码,其实就是简单对基因序列进行交换、移位、翻转等操作。
浮点数编码则可能产生介于中间的值,或者其他。
变异/突变
二进制编码体现在某个或多个位以一定概率取反。
浮点数编码体现在随机增加或减小一个步长,步长开始大,后面小,动态改变步长,尽可能加快收敛,同时保证能收敛到精确的点上。
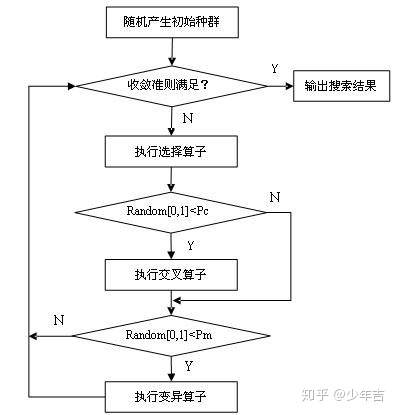
题目实践
问题
\(f(x)=2*\sin{(x)}+\cos{(x)}\)的最大值
求解完整代码
代码来自参考中,比较详尽,可以直接运行,可能要去掉第3和7行。
轮盘赌部分没看懂,抽奖的方法,转盘转。
函数作用表
| 函数 | 作用 |
|---|---|
| species_origin | 返回个体数*基因数的矩阵population |
| translation | 输入population,得到每个个体基因的十进制数的1*population_size的矩阵 |
| function | 输入population,得到每个个体的适应度\(f(x)\)一维数组 |
| fitness | 对function输入结果进行过滤,小于0的变为0(没看懂,可能是因为要计算适应度的和) |
| cumsum | 输入fitness结果,输出各适应度所占的区间,依次增大,最后一个为1 |
| selection | 输入population和fitness,根据轮盘赌算法输出新的种群 |
| crossover | 输入population,基因的交叉操作,每相邻两个个体之间交换基因 |
| mutation | 变异操作,根据pm,在某一位置上取反 |
| b2d | 取最大值函数 |
完整代码
点击查看代码
# -*-coding:utf-8 -*-
#目标求解2*sin(x)+cos(x)最大值
%matplotlib notebook
import random
import math
import matplotlib.pyplot as plt
%matplotlib inline
class GA(object):
#初始化种群 生成chromosome_length大小的population_size个个体的种群
def __init__(self,population_size,chromosome_length,max_value,pc,pm):
self.population_size=population_size
self.choromosome_length=chromosome_length
# self.population=[[]]
self.max_value=max_value
self.pc=pc
self.pm=pm
# self.fitness_value=[]
def species_origin(self):
population=[[]]
for i in range(self.population_size):
temporary=[]
#染色体暂存器
for j in range(self.choromosome_length):
temporary.append(random.randint(0,1))
#随机产生一个染色体,由二进制数组成
population.append(temporary)
#将染色体添加到种群中
return population[1:]
# 将种群返回,种群是个二维数组,个体和染色体两维
#从二进制到十进制
#编码 input:种群,染色体长度 编码过程就是将多元函数转化成一元函数的过程
def translation(self,population):
temporary=[]
for i in range(len(population)):
total=0
for j in range(self.choromosome_length):
total+=population[i][j]*(math.pow(2,j))
#从第一个基因开始,每位对2求幂,再求和
# 如:0101 转成十进制为:1 * 20 + 0 * 21 + 1 * 22 + 0 * 23 = 1 + 0 + 4 + 0 = 5
temporary.append(total)
#一个染色体编码完成,由一个二进制数编码为一个十进制数
return temporary
# 返回种群中所有个体编码完成后的十进制数
#from protein to function,according to its functoin value
#a protein realize its function according its structure
# 目标函数相当于环境 对染色体进行筛选,这里是2*sin(x)+math.cos(x)
def function(self,population):
temporary=[]
function1=[]
temporary=self.translation(population)
for i in range(len(temporary)):
x=temporary[i]*self.max_value/(math.pow(2,self.choromosome_length)-10)
function1.append(2*math.sin(x)+math.cos(x))
#这里将sin(x)作为目标函数
return function1
#定义适应度
def fitness(self,function1):
fitness_value=[]
num=len(function1)
for i in range(num):
if(function1[i]>0):
temporary=function1[i]
else:
temporary=0.0
# 如果适应度小于0,则定为0
fitness_value.append(temporary)
#将适应度添加到列表中
return fitness_value
#计算适应度和
def sum(self,fitness_value):
total=0
for i in range(len(fitness_value)):
total+=fitness_value[i]
return total
#计算适应度斐伯纳且列表
def cumsum(self,fitness1):
for i in range(len(fitness1)-2,-1,-1):
# range(start,stop,[step])
# 倒计数
total=0
j=0
while(j<=i):
total+=fitness1[j]
j+=1
fitness1[i]=total
fitness1[len(fitness1)-1]=1
#3.选择种群中个体适应度最大的个体
def selection(self,population,fitness_value):
new_fitness=[]
#单个公式暂存器
total_fitness=self.sum(fitness_value)
#将所有的适应度求和
for i in range(len(fitness_value)):
new_fitness.append(fitness_value[i]/total_fitness)
#将所有个体的适应度正则化
self.cumsum(new_fitness)
#
ms=[]
#存活的种群
population_length=pop_len=len(population)
#求出种群长度
#根据随机数确定哪几个能存活
for i in range(pop_len):
ms.append(random.random())
# 产生种群个数的随机值
# ms.sort()
# 存活的种群排序
fitin=0
newin=0
new_population=new_pop=population
#轮盘赌方式
while newin<pop_len:
if(ms[newin]<new_fitness[fitin]):
new_pop[newin]=population[fitin]
newin+=1
else:
fitin+=1
population=new_pop
#4.交叉操作
def crossover(self,population):
#pc是概率阈值,选择单点交叉还是多点交叉,生成新的交叉个体,这里没用
pop_len=len(population)
for i in range(pop_len-1):
if(random.random()<self.pc):
cpoint=random.randint(0,len(population[0]))
#在种群个数内随机生成单点交叉点
temporary1=[]
temporary2=[]
temporary1.extend(population[i][0:cpoint])
temporary1.extend(population[i+1][cpoint:len(population[i])])
#将tmporary1作为暂存器,暂时存放第i个染色体中的前0到cpoint个基因,
#然后再把第i+1个染色体中的后cpoint到第i个染色体中的基因个数,补充到temporary2后面
temporary2.extend(population[i+1][0:cpoint])
temporary2.extend(population[i][cpoint:len(population[i])])
# 将tmporary2作为暂存器,暂时存放第i+1个染色体中的前0到cpoint个基因,
# 然后再把第i个染色体中的后cpoint到第i个染色体中的基因个数,补充到temporary2后面
population[i]=temporary1
population[i+1]=temporary2
# 第i个染色体和第i+1个染色体基因重组/交叉完成
def mutation(self,population):
# pm是概率阈值
px=len(population)
# 求出种群中所有种群/个体的个数
py=len(population[0])
# 染色体/个体基因的个数
for i in range(px):
if(random.random()<self.pm):
mpoint=random.randint(0,py-1)
#
if(population[i][mpoint]==1):
#将mpoint个基因进行单点随机变异,变为0或者1
population[i][mpoint]=0
else:
population[i][mpoint]=1
#transform the binary to decimalism
# 将每一个染色体都转化成十进制 max_value,再筛去过大的值
def b2d(self,best_individual):
total=0
b=len(best_individual)
for i in range(b):
total=total+best_individual[i]*math.pow(2,i)
total=total*self.max_value/(math.pow(2,self.choromosome_length)-1)
return total
#寻找最好的适应度和个体
def best(self,population,fitness_value):
px=len(population)
bestindividual=[]
bestfitness=fitness_value[0]
# print(fitness_value)
for i in range(1,px):
# 循环找出最大的适应度,适应度最大的也就是最好的个体
if(fitness_value[i]>bestfitness):
bestfitness=fitness_value[i]
bestindividual=population[i]
return [bestindividual,bestfitness]
def plot(self, results):
X = []
Y = []
for i in range(500):
X.append(i)
Y.append(results[i][0])
plt.plot(X, Y)
plt.show()
def main(self):
results = [[]]
fitness_value = []
fitmean = []
population = pop = self.species_origin()
for i in range(500):
function_value = self.function(population)
# print('fit funtion_value:',function_value)
fitness_value = self.fitness(function_value)
# print('fitness_value:',fitness_value)
best_individual, best_fitness = self.best(population,fitness_value)
results.append([best_fitness, self.b2d(best_individual)])
# 将最好的个体和最好的适应度保存,并将最好的个体转成十进制,适应度函数
self.selection(population,fitness_value)
self.crossover(population)
self.mutation(population)
results = results[1:]
results.sort()
self.plot(results)
if __name__ == '__main__':
population_size=400#种群大小
max_value=10#x的最大值,x是表现型,由基因构造的比率乘以最大值得到,其他情况下是乘以区间长度加上最小值
chromosome_length=20#基因的位数,采用二进制编码
pc=0.6#交叉中的概率阈值,但是这个代码貌似并没有用
pm=0.01#突变的概率,突变时使用random生成一个概率和它比较
ga=GA(population_size,chromosome_length,max_value,pc,pm)
ga.main()
运行结果
500次每次的最大\(f(x)\),可以清除看到每次都在上升,但是貌似并没有标注是哪个\(x\)生成的。
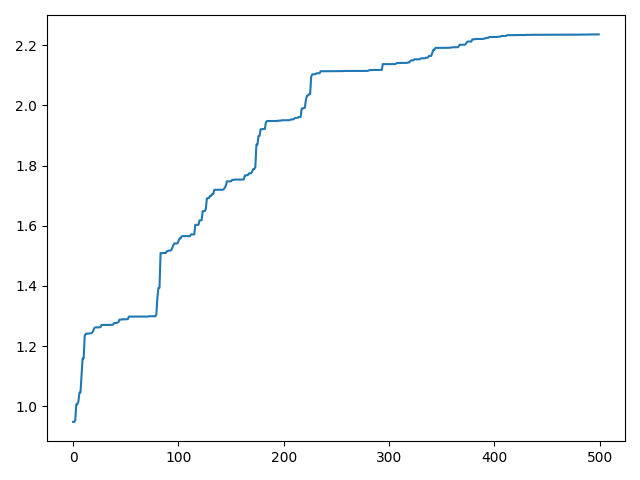
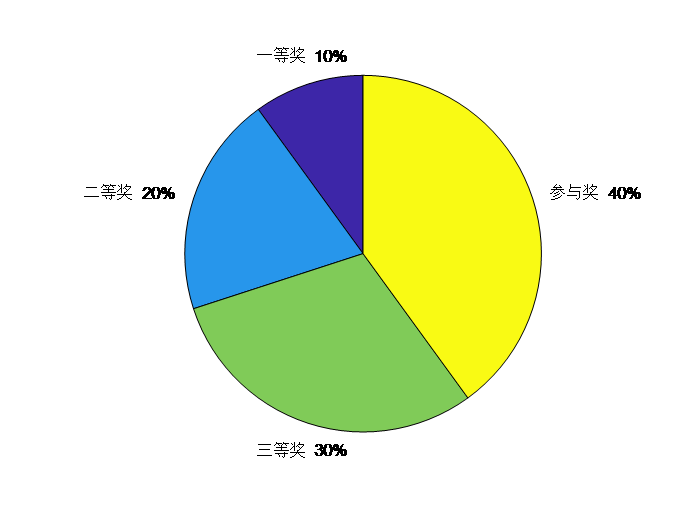
轮盘赌算法
因为前面的轮盘赌算法没看懂,又去找博客看了看。
个人理解:假设有一个转盘和指针,指针转动一圈停留在哪个区间就是哪个。指针转动可以使用随机函数random.random模拟,随机落到0-1的区间,落在哪个区间对应的方案就是哪个。构造区间我们使用
$$q_i=\sum_{j=0}^{i}P(x_j)$$
\(P(x_j)\)是\(x_j\)被选中的概率,依次生成\(0,q_1,q_2,q_3,\cdots,q_n,1\),随机一个概率\(r\),落在哪个区间就是哪个。例如\(q_2<r<q_3\),则选中了\(x_3\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号