DFQ——前后两层卷积核数量不一样是否可以进行均衡

1 问题：前后两层卷积核数量不一样是否可以进行均衡，均衡到底是对什么进行均衡

我以前一直以为是前后两个相邻层做均衡的时候是卷积核上进行。这部分原理的描述在论文中的描述在4.1.1


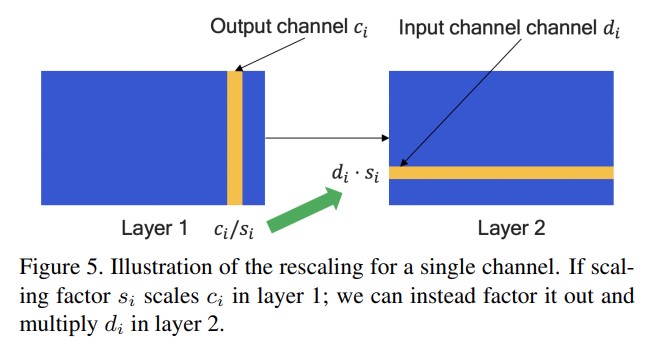
从公式上我们可以看到缩放因子S是直接乘在W上的，W是啥，不就是参数么，也就是卷积核。尤其是white paper上面这个插图，更是直接把东西标在了权重矩阵上。我很自然想那就是按照卷积核来进行均衡呗。上面黄色的那一条和下面蓝色的那一条不就是某一个卷积核。这样理解都自然

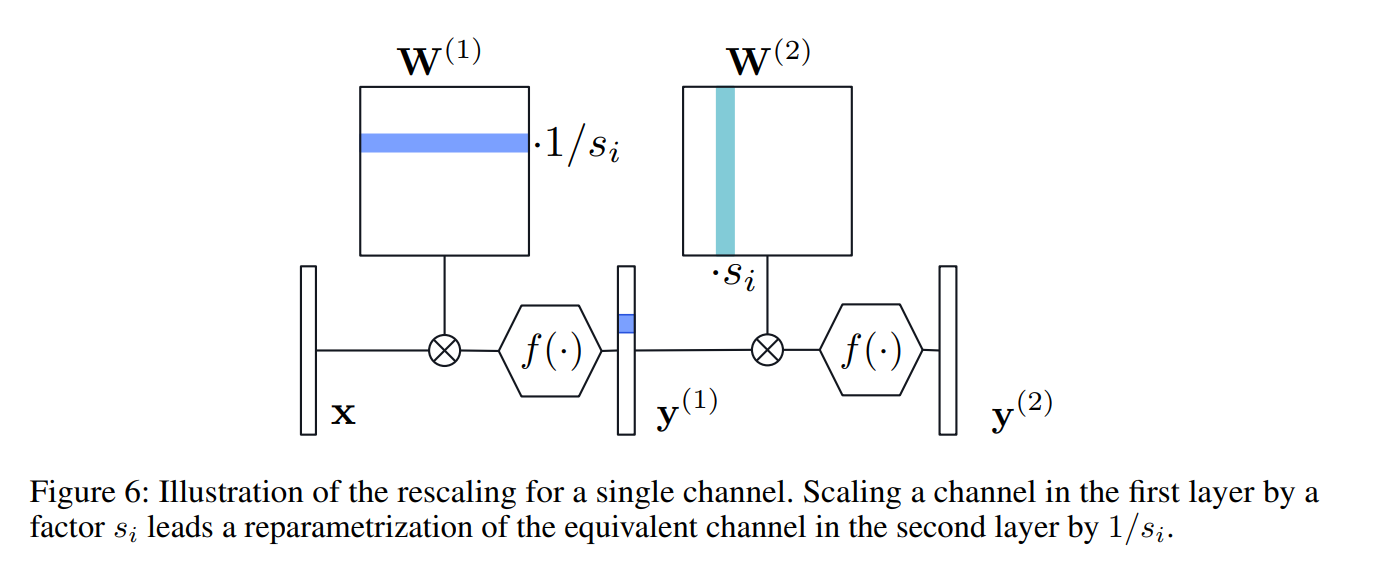
之前我都是这么想的，现在在实现的时候觉得不对，因为我们求s时，我们是对应两个层之间进行，那如果卷积核数量不一样多，那富余出来的那些卷积核怎么办呢？而且大多数情况下前后两层的卷积核数量相等是一个少见的情况，大部分情况应该都是不相等的。

2 卷积核在代码中的表现形式

我和宇泽的讨论是前一层的输出和下一层的输入他们的层数是一样的。这里输入、输出值得就是训练数据在网络里在不同的位置所得到的值。

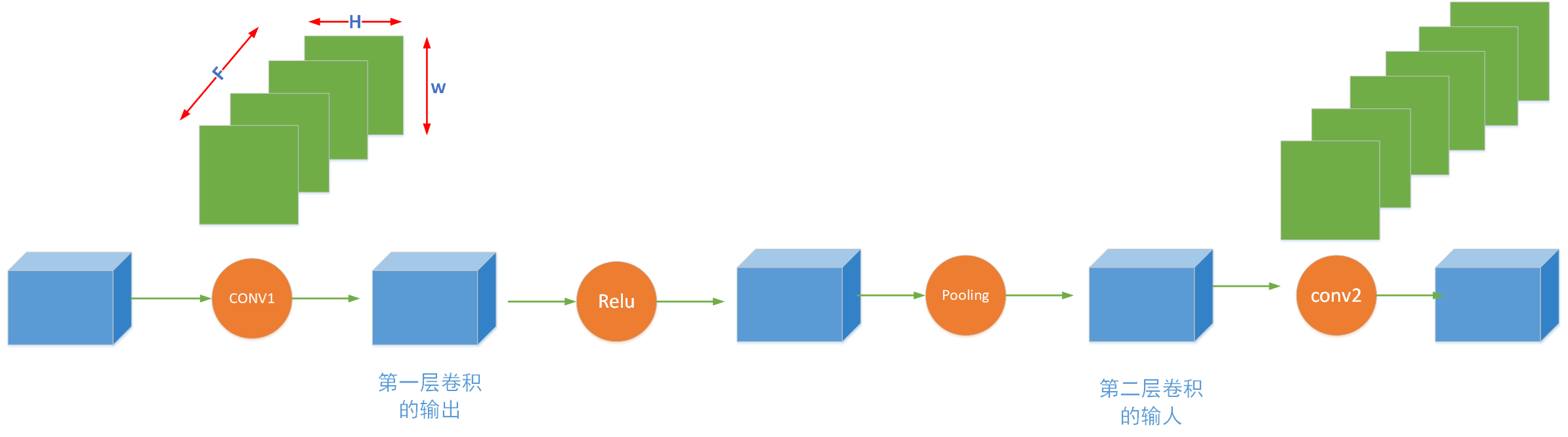
比如说在这个图中，第一层卷积的输出应该是一个数据体，在送到第二层卷积之前还会过一些层比如relu或者pooling但是都不会改变通道数，难道是在这两个数据体上做均衡？但是代码中我们明显是在weight上进行均衡

那这是怎么回事呢？
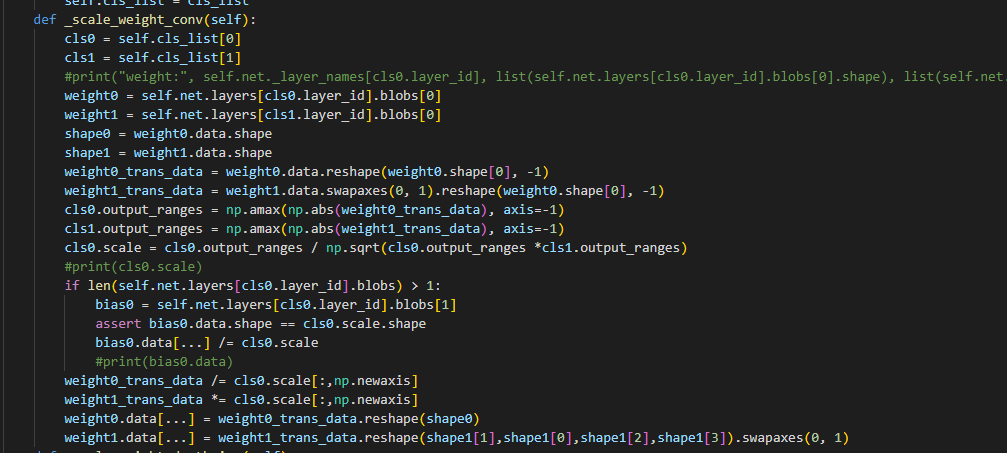
经过单步调试，我知道问题的所在。是我对于卷积核在代码中的表现形式理解有偏差
我以前总以为卷积核由三个尺寸，F（卷积核的个数），积核的高H，宽W。
其实卷积核是由四个数字构成，单个卷积核的尺寸以及卷积核的个数。单个卷积核包括宽W，高H，以及深度C（或者通道数）。因为一个卷积也是一个立方体。
不少教材在介绍卷积的时候更多的是关注卷积之后如何确定输出数据的单层featuremap的尺寸，我只需要输入数据体的H，W，以及卷积核H，W，stride，Pad，就行了，确实不需要通道数，因为默认输入数据的通道数和卷积核的通道数是一样的。久而久之我就忘了这点。
不管是在caffe还是在pytroch上卷积核由四个数确定（F, C, H, W）

3 一些数量关系

因为在prototxt上是不会出现训练数据的，但是尺寸信息是非常重要的信息，我们自己心里要清楚这个尺寸是怎么来的。我找到了一份手动实现卷积过程的代码，这里有各种细节。

def conv_forward_naive(x, w, b, conv_param):
    """
    A naive implementation of the forward pass for a convolutional layer.

    The input consists of N data points, each with C channels, height H and
    width W. We convolve each input with F different filters, where each filter
    spans all C channels and has height HH and width WW.

    Input:
    - x: Input data of shape (N, C, H, W)
    - w: Filter weights of shape (F, C, HH, WW)
    - b: Biases, of shape (F,)
    - conv_param: A dictionary with the following keys:
      - 'stride': The number of pixels between adjacent receptive fields in the
        horizontal and vertical directions.
      - 'pad': The number of pixels that will be used to zero-pad the input. 


    During padding, 'pad' zeros should be placed symmetrically (i.e equally on both sides)
    along the height and width axes of the input. Be careful not to modfiy the original
    input x directly.

    Returns a tuple of:
    - out: Output data, of shape (N, F, H', W') where H' and W' are given by
      H' = 1 + (H + 2 * pad - HH) / stride
      W' = 1 + (W + 2 * pad - WW) / stride
    - cache: (x, w, b, conv_param)
    """
    out = None
    ###########################################################################
    # TODO: Implement the convolutional forward pass.                         #
    # Hint: you can use the function np.pad for padding.                      #
    ###########################################################################
    pad = conv_param['pad']
    stride = conv_param['stride']
    N, C, H, W = x.shape
    F, C, FH, FW = w.shape

    assert (H - FH + 2 * pad) % stride == 0
    assert (W - FW + 2 * pad) % stride == 0
    #outH = 1 + (H - FH + 2 * pad) / stride
    #outW = 1 + (W - FW + 2 * pad) / stride
    outH = int(1 + (H - FH + 2 * pad) / stride)
    outW = int(1 + (W - FW + 2 * pad) / stride)


    # create output tensor after convolution layer
    out = np.zeros((N, F, outH, outW))

    # padding all input data
    x_pad = np.pad(x, ((0,0), (0,0),(pad,pad),(pad,pad)), 'constant')
    H_pad, W_pad = x_pad.shape[2], x_pad.shape[3]    

    # create w_row matrix
    w_row = w.reshape(F, C*FH*FW)                            #[F x C*FH*FW]

    # create x_col matrix with values that each neuron is connected to
    x_col = np.zeros((C*FH*FW, outH*outW))                   #[C*FH*FW x H'*W']
    for index in range(N):
        neuron = 0 
        for i in range(0, H_pad-FH+1, stride):
            for j in range(0, W_pad-FW+1,stride):
                x_col[:,neuron] = x_pad[index,:,i:i+FH,j:j+FW].reshape(C*FH*FW)
                neuron += 1
        out[index] = (w_row.dot(x_col) + b.reshape(F,1)).reshape(F, outH, outW)
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x_pad, w, b, conv_param)
    return out, cache

3.1 输入数据、卷积层、输出数据的数量关系

一个输入数据的shape是(N, C, H, W) 。N是这一批次中图片的数量。
处理这个数据的卷积层shape是(F, C, H, W)。
那么输出数据的shape是(F, C, oH, oW)。oH和oW是输出数据体宽和高。

3.2 相邻两层的数量关系

假设前一层卷积层的尺寸为 $(F^{(i)},C^{(i)},H^{(i)},W^{(i)})$
后一层卷积的尺寸为 $(F^{(i+1)},C^{(i+1)},H^{(i+1)},W^{(i+1)})$
一般来说存在这样的关系。$C^{(i+1)}=F^{(i)}$

4 前后两层卷积均衡的具体做法

在Numpy中存在这样一种操作，对高维数据体的维度进行交换。其实这就是把数据在空间上进行重新的排布。
卷积层也可以看成包含四个维度的数据体，我们可以对其进行维度变换。
特别是当我们把后一层卷积的第一个维度和第二个维度进行调换之后。
$(F^{(i+1)},C^{(i+1)},H^{(i+1)},W^{(i+1)})$变成$(C^{(i+1)},F^{(i+1)},H^{(i+1)},W^{(i+1)})$
这样便和前一层卷积的数据进行了对齐
第一层：$(F^{(i)},C^{(i)},H^{(i)},W^{(i)})$
第二层：$(C^{(i+1)},F^{(i+1)},H^{(i+1)},W^{(i+1)})$
根据上一小节3.2，这两个数组的第一个维度是一样的
我们再将后面三个维度抻平成一个一维的向量，变成
第一层：$(F^{(i)},C^{(i)}\ast H^{(i)}\ast W^{(i)})$ 和
第二层：$(C^{(i+1)},F^{(i+1)}\ast H^{(i+1)}\ast W^{(i+1)})$
之后再求第二维的最大值，这不就是r嘛
第一层：$(F^{(i)},r^{(i)}=max(C^{(i)}\ast H^{(i)}\ast W^{(i)}))$ 和
第二层：$(C^{(i+1)},r^{(i+1)}max(F^{(i+1)}\ast H^{(i+1)}\ast W^{(i+1)}))$

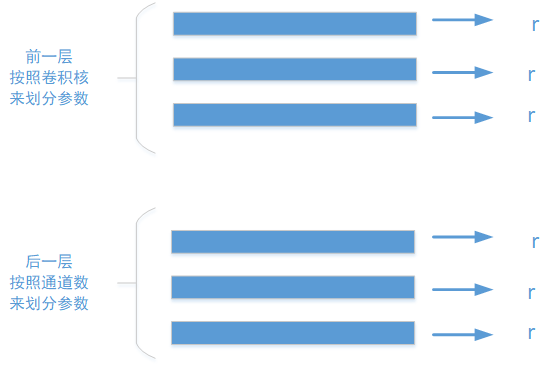
这其实相当于前一层卷积的参数按照卷积核来进行划分，后一层卷积的参数按照通道数来进行重新划分。

来自为知笔记(Wiz)