机器学习——神经网络

一、神经网络：

1.1非线性假设：

无论是线性回归还是逻辑回归都有这样一个缺点，即：当特征太多时，计算的负荷会非常大。

使用非线性的多项式项，能够帮助我们建立更好的分类模型 ，但与此同时他们的特征组合就有很多。普通的线性模型无法处理，就需要神经网络。

1.2模型表示1

每一个神经元都可以被认为是一个处理单元/神经核（processing unit/Nucleus），它含有许多输入/树突（input/Dendrite），并且有一个输出/轴突（output/Axon）.神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。

每一个神经元又是一个学习模型。这些神经元（也叫激活单元，activation unit）采纳一些特征作为输出，并且根据本身的模型提供一个输出。

神经元图：

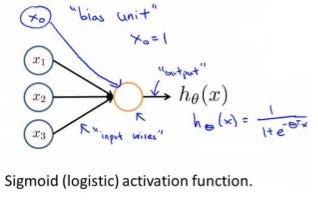
神经网络图：

其中：第一层成为输入层（Input Layer），最后一层称为输出层（Output Layer），中间一层成为隐藏层（Hidden Layers） 。

一般我们为每一层都增加一个偏差单位（bias unit）然后每层的一个节点都有自己的权重，这样其实就是等价于一个线性模型:y=kx+b;

\(a_i^{(j)}\) 代表第j层的第i个激活单元，\(\theta^{(j)}\) 代表从第j层映射到第j+1层时的权重矩阵。

对于

特征矩阵的一行给了神经网络，得到\(\theta*X=a\);

1.3模型表示2

利用向量化的方法会使得计算更方便：\(a^{(i)}=g(\theta^{(i-1)}a^{(i-1)})\) (其中每次计算完，都要在后面加一个\(a_0^{(i)}=1\),其中\(a^{(0)}=x\) )

如果是整个训练集的话：\(a^{(i)}=g(\theta^{(i-1)}a^{(i-1)}) 其中a^{(0)}=X^T\) (需要使得每一列是特征)

如果遮住左半部分，其实就是逻辑回归；（别忘了加个\(a_0^{(2)}\) =1），其实\(a^{(2)}\) 是更高级的特征，他们是X决定的，这些特征值比x次方厉害很多，也能更好地预测新数据。

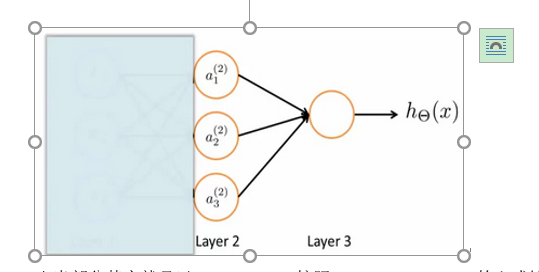
1.4多类分类

当我们有不止两种分类时（也就是y=1,2,3...k）,输出就是k个维度，是哪一类，哪一个位置就是1，其余全为1.

如\(\left [ \begin{matrix}1\\0\\0\\0\end{matrix}\right]\)

二、神经网络的学习

2.1代价函数

符号说明：

m：样本个数

(x,y)：一组输入输出

L：神经网络层数

\(L_l\)： 每层的神经元个数

\(S_L\) ：最后一层中处理单元的个数

二分类：\(S_L=1\) ,y=0 or 1代表哪一类；

K 类分类 ：\(S_L=k\) ,\(y_i=1\) 表示分到第i类；

代价函数：

\[J(\theta)=-\frac{1}{m}[\sum_{i=1}^m\sum_{k=1}^ky_k^{(i)}log(h_\theta(x^{(i)}))_k+(1-y_k^{(i)})log(1-(h_\theta(x^{(i)}))_k)+\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_{l+1}}(\theta_{ji}^{(l)})^2] \]

2.2反向传播算法

2.2.1算法概述：

为了计算代价函数的偏导数\(\frac{\partial}{\partial\theta_{ij}^{(l)}}J(\theta)\) ,需要从后面一层一层反向求出各层的误差。

假设：\(K=4,S_L=4,L=4;\)

那么：\(\delta^{(4)}=a^{(4)}-y;\\\delta^{(3)}=(\theta^{(3)})^T\delta^{(4)}g'(z^{(3)})，其中g'(z^{(3)})=a^{(3)}*(1-a^{(3)})\)

如果不做任何正则化处理，那么\(\frac{\partial}{\partial\theta_{ij}^{(l)}}J(\theta)=a_j^{(l)}\delta_i^{l+1}\)

\(l\):目前所计算的是第几层；

j:目前计算层中的激活单元的下标，也将是下一层的第j个输入变量的下标

i:代表下一层中误差单元的下标，是收到权重矩阵中的第i行影响的下一层中的误差单元的下标

训练集为矩阵:

\(D_{ij}^{(l)}=\frac{\partial}{\partial\theta_{ij}^{(l)}}J(\theta)\)就是要计算的偏导数；

2.2.2反向传播的直观理解：

参考网站：

http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

2.3梯度检验：

模型较为复杂时，可能存在不易察觉的错误。我们用梯度的数值检验这样的错误。

通过计算\(\theta\)两边很近的代价值构成的直线的斜率来估计该点的梯度值。

如对\(\theta_1进行检验\)

2.4神经网络流程：

我们真正要决定的是隐藏层的层数和每个中间层的单元数。

训练神经网络：

1. 参数的随机初始化
2. 利用正向传播方法计算所有的 \(h_\theta(x)\)
3. 编写计算代价函数\(J\)的代码
4. 利用反向传播方法计算所有偏导数
5. 利用数值检验方法检验这些偏导数
6. 使用优化算法来最小化代价函数!