图论篇1——图的基本概念
图的基本性质
顶点(vertex)
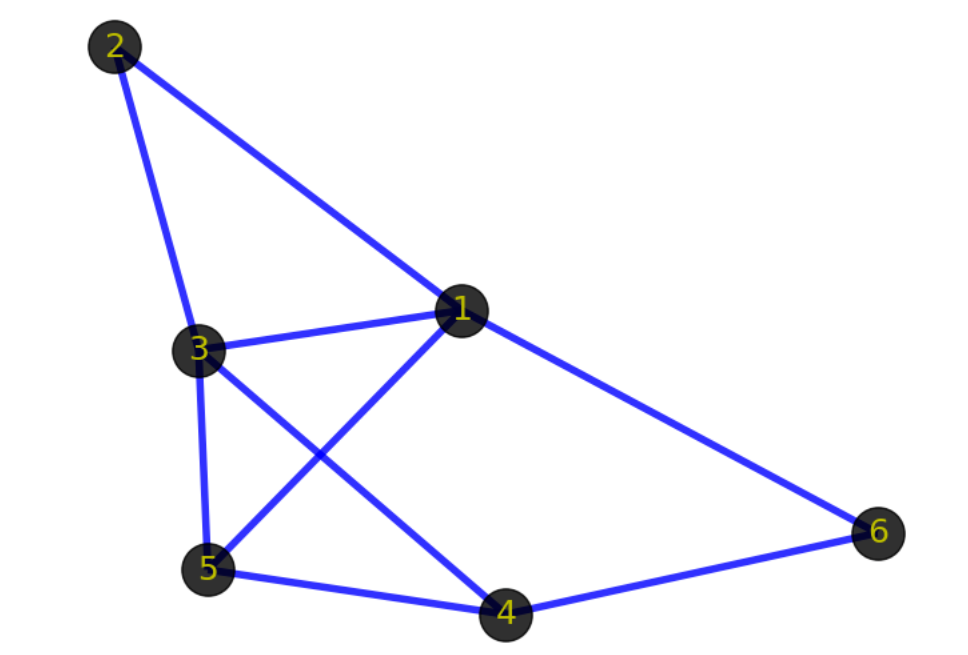
上图中黑色的带数字的点就是顶点,表示某个事物或对象。由于图的术语没有标准化,因此,称顶点为点、节点、结点、端点等都是可以的。叫什么无所谓,理解是什么才是关键。
边(edge)
上图中顶点之间蓝色的线条就是边,表示事物与事物之间的关系。需要注意的是边表示的是顶点之间的逻辑关系,粗细长短都无所谓的。包括上面的顶点也一样,表示逻辑事物或对象,画的时候大小形状都无所谓。
有向/无向图(Directed Graph/ Undirected Graph)
有向图和无向图,两者的区别在于,有向图中的边是有方向性的。(可以把无向图视为“双向”的有向图,构造无向图用的就是这种方法)
一般到底是有向图还是无向图要根据实际情况判断,比如在A、B两点之间的一条路,那一定是个无向图。
权重(weight)
边的权重(或者称为权值、开销、长度等),即每条边都有与之对应的值。例如当顶点代表某些地点时,两个顶点间边的权重可以为两点的距离。
连通图/连通分量(connected graph/connected component)
如果在图G中,任意2个顶点之间都存在路径,那么称G为连通图(注意是任意2顶点)。如果把下图看为两个图,就是两个连通图。
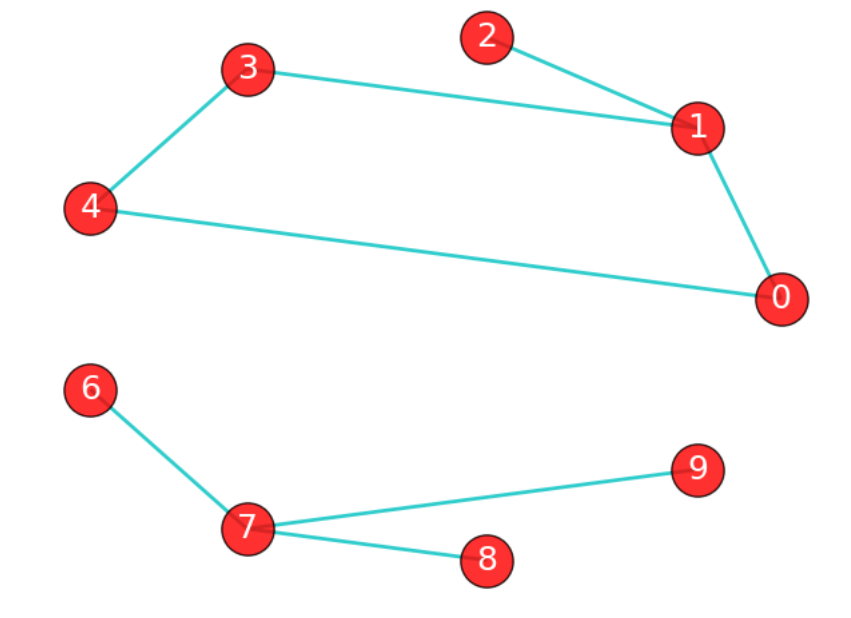
连通分量也叫最(极)大连通子图,把上图看为一个整体,它不是一个连通图,但它有多个连通子图,0,1,2,3,4顶点构成的子图就是该图的最大连通子图。
注意:对于连通图来说,它的最大连通子图就是其本身。
图的表示
邻接矩阵
用二维数组直接存储。
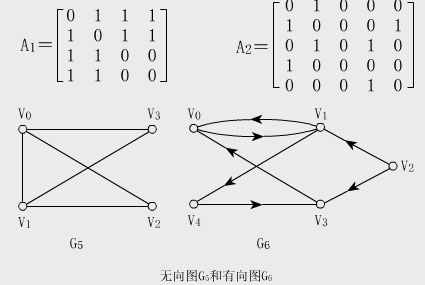
邻接矩阵非常好写,只需要开一个二维数组,但顶点数目太大会超内存(一般不大于1000),用到的情况比较少。
邻接表
存储示意图:
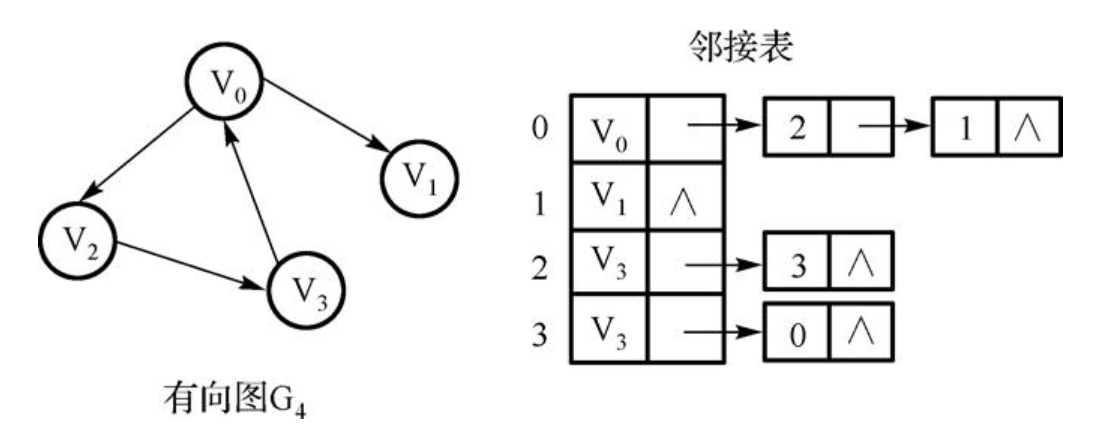
可理解看做是多条单链表,结构体定义如下:
struct ENode { int dis, to;//权重、指向 ENode* next = NULL; void push(int to, int dis) { ENode* p = new ENode; p->to = to; p->dis = dis; p->next = next; next = p; } }head[100];
完整测试:
#include <iostream> #include <fstream> using namespace std; typedef long long LL; struct ENode { int dis, to;//权重、指向 ENode* next = NULL; void push(int to, int dis) { ENode* p = new ENode; p->to = to; p->dis = dis; p->next = next; next = p; } }*head; int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL /* 5 8 1 3 4 2 4 3 4 5 6 1 5 7 3 5 4 3 4 3 2 5 6 4 1 7 */ int n, m; //n个定点,m条边 cin >> n >> m; head = new ENode[n + 1]; for (int i = 0; i < m; i++) { int from, to, dis; cin >> from >> to >> dis; head[from].push(to, dis); } for (int i = 1; i <= n; i++) { cout << i; ENode* p = head[i].next; while (p) { if (p)cout << "-->"; cout << p->to; p = p->next; } cout << endl; } return 0; }
其他一些术语
关节点
也叫重连通分量,在连通图 G 中,如果删除顶点 u 及从 u 出发的所有边后所得的子图不连通,我们就称顶点 u 为图 G 的关节点或连接点。
生成树
树(Tree):如果一个无向连通图中不存在回路,则这种图称为树。
生成树 (Spanning Tree):无向连通图G的一个子图如果是一颗包含G的所有顶点的树,则该子图称为G的生成树。
生成树是连通图的极小连通子图。这里所谓极小是指:若在树中任意增加一条边,则将出现一条回路;若去掉一条边,将会使之变成非连通图。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号