Vjudge 3.14 训练解题报告
比赛传送门 \(\color{white}{password:3.1415926}\)
A. Fibonacci-ish
题意:定义一个序列为“Fibonacci-ish”的,当且仅当对任意 \(2< i\le n,a_i=a_{i-1}+a_{i-2}\)。给定一个长为 \(n\) 的数组,求选出若干个元素重新排列,形成“Fibonacci-ish”的序列的最长长度。\(n\le 1000,V\le 10^9\)。
首先有一个暴力做法,\(n^2\) 枚举两个起点,然后后面的元素都可确定。思考可以发现,这个暴力其实是正确的,因为斐波那契数的增长速度是指数级的,自然长度是 \(\log\) 级的,所以暴力跑的复杂度为 \(O(n^2\log^2n)\)。需要注意特判两个起点均为 \(0\) 的情况,此时答案为 \(cnt_0\)。
By zhouhaoxu
#include<bits/stdc++.h>
#define int long long
#define N 200005
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
using namespace std;
int n,a[N],ans; map<int,int>cn; vector<int>vi;
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]),cn[a[i]]++,ans+=(a[i]==0);
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
if(i==j) continue; if(a[i]==0&&a[j]==0) continue; vi.clear(),vi.pb(a[i]),vi.pb(a[j]);
cn[a[i]]--,cn[a[j]]--; int p=a[i]+a[j],ret=2,lst=a[j]; while(p<=(int)2e9&&p>=(int)-2e9&&cn[p]){
cn[p]--,vi.pb(p); int t=lst+p; lst=p,p=t,++ret;
}for(int &u:vi) cn[u]++; ans=max(ans,ret);
}return !printf("%lld\n",ans);
}
B. Grime Zoo
题意:给定一个含问号的 01 串,你需要将所有问号改为 0 或 1,定义代价为 01 的子序列数 \(\times x\) 加上 10 的子序列数 \(\times y\)。最小化代价。\(n\le 10^5\)
直接考虑非常复杂,所以考虑挖掘性质。可以猜想,如果 01 的代价较大,则要尽可能把前面填 1,后面填 0;反之则尽可能前面填 0,后面填 1。
这种贪心看起来比较假,但实际上不难证明为真:假设 01 的代价 \(x\) 较大,使用反证法,假设最优方案中有一个问号填 0 在填 1 前面,证明交换此 01 更优:
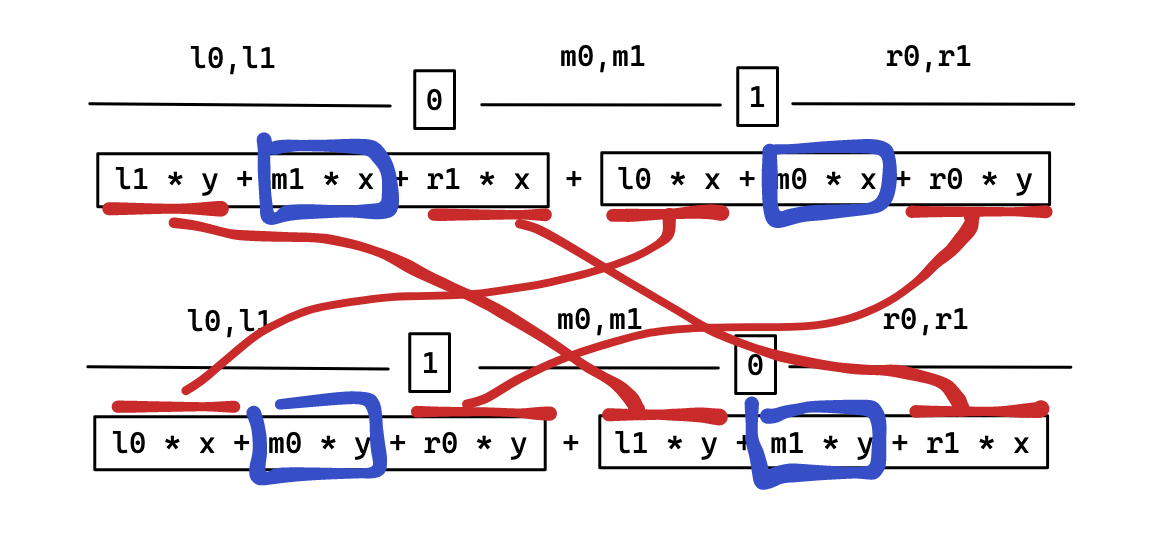
更感性一点的证明是,交换两位对左右两边来说没有影响,因为在他们看来,都是同一侧有一个 0 一个 1,交换位置没有影响。但对中间来说,一个是左 0 右 1,一个是左 1 右 0,自然后者更优。
于是,我们假设要左边填 1 右边填 0(反之则 01 取反即可),考虑如何计算答案。首先预处理出数字与数字之间的贡献 \(sum\)(即不考虑问号),然后预处理一些必要信息(如前缀 0,1,? 的个数 \(s_0(i),s_1(i),s_?(i)\))。接下来,使用递推的方式处理出从 \(1\) 走到 \(i\) 全填 1 在左边的贡献 \(l(i)\),以及从 \(n\) 走到 \(i\) 全填 0 在右边的贡献 \(r(i)\)。最后枚举分界线,答案为 \(sum+l(i)+r(i+1)+左?1对右0+右?0对左1\)。
预处理 \(l(i),r(i)\) 的原因是,左边的 ?1 对右边的 0 的贡献容易计算,因为右边所有的 0 都在 ?1 的右侧,但左边的 ?1 对左边的 0 的贡献较难直接计算,因为不同的 ?1 左边 0 的个数并不相同,需要递推处理。
By cxm1024
#include <bits/stdc++.h>
using namespace std;
#define int long long
int s1[100010], s0[100010], s2[100010];
int l[100010], r[100010];
signed main() {
string s;
int x, y;
cin >> s >> x >> y;
int n = s.size();
s = " " + s;
if (y > x) {
for (int i = 1; i <= n; i++) {
if (s[i] == '1') s[i] = '0';
else if (s[i] == '0') s[i] = '1';
}
swap(x, y);
}
for (int i = 1; i <= n; i++) {
s1[i] = s1[i - 1] + (s[i] == '1');
s0[i] = s0[i - 1] + (s[i] == '0');
s2[i] = s2[i - 1] + (s[i] == '?');
}
int res = 0;
for (int i = 1; i <= n; i++)
if (s[i] == '1')
res += s0[i - 1] * x + (s0[n] - s0[i]) * y;
for (int i = 1; i <= n; i++) {
l[i] = l[i - 1];
if (s[i] == '?') l[i] += s0[i - 1] * x + (s0[n] - s0[i]) * y;
}
for (int i = n; i > 0; i--) {
r[i] = r[i + 1];
if (s[i] == '?') r[i] += (s1[n] - s1[i]) * x + s1[i - 1] * y;
}
int ans = r[1];
for (int i = 1; i <= n; i++) {
if (s[i] == '?') ans = min(ans, l[i] + r[i + 1] + s2[i] * (s2[n] - s2[i]) * y);
}
cout << ans + res << endl;
return 0;
}
C. Vasily the Bear and Sequence
题意:给一个长度为 \(n\) 的数组,你需要选出一些元素,使他们按位与后的
lowbit尽量大(定义lowbit(0)=-1),在此基础上元素尽可能多。\(n\le 10^5,V\le 10^9,V\ne V\)
显然可以枚举钦定 lowbit,然后判定是否可行。如果 lowbit 钦定为第 \(i\) 位,则选的元素的第 \(i\) 位只能为 \(1\)(一旦有 \(0\) 就会被与成 \(0\))。然后就是要让更低的位变成 \(0\),容易发现与的元素越多越容易变成 \(0\),所以最优一定是把所有第 \(i\) 位为 \(1\) 的元素全部选上。
By cxm1024
#include <bits/stdc++.h>
using namespace std;
int n, a[100010];
signed main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
vector<int> ans;
int maxn = -1;
for (int i = 0; i <= 30; i++) {
vector<int> v;
for (int j = 1; j <= n; j++)
if (a[j] >> i & 1) v.push_back(a[j]);
if (v.empty()) continue;
int res = v[0];
for (int j : v) res &= j;
if ((res & -res) > maxn)
ans = v, maxn = (res & -res);
}
printf("%lu\n", ans.size());
for (int x : ans) printf("%d ", x);
return 0;
}
D. Mike and Frog
题意:有两个变量,第 \(0\) 秒为 \(h_1,h_2\),每秒 \(h_1\leftarrow x_1h_1+y_1\bmod m,h_2\leftarrow x_2h_2+y_2\bmod m\),问最早使 \(h_1=a_1\) 且 \(h_2=a_2\) 的时刻是多少。\(m\le 10^6,0\le h,a,x,y<m,h\ne a\)
显然问题的关键在于形成的环。两个元素都会在若干步之后进入环,所以可以暴力跑 \(m\) 步,处理出进入之前的长度和环的长度,同时顺便处理好了目标位置不在环上的情况。以下只需要考虑目标在环上。
假设两个环长分别为 \(len_1,len_2\),目标在环上的位置分别为 \(b_1,b_2\),环之前的长度为 \(t_1,t_2\),则两个变量同时满足要求的时刻 \(x\) 满足:
看起来需要使用 exgcd 来解同余方程,但其实并不需要,可以如下操作:
因为 \(x-t_1\equiv b_1\pmod m\),所以 \(x=km+b_1+t_1\)。感性理解一下可以发现,随着 \(k\) 的变化,在第二个同余式中的结果同样会形成一个不超过 \(m\) 的环。于是直接 \(O(m)\) 枚举 \(k\) 检验是否合法即可。
By zhouhaoxu
#include<bits/stdc++.h>
#define int long long
#define N 2000005
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
using namespace std;
int l[2],m,h[2],a[2],x[2],y[2],p[2],t[N],vs[N],ls[N],th[2];
signed main(){
scanf("%lld",&m); for(int i=0;i<2;i++)
scanf("%lld%lld%lld%lld",&h[i],&a[i],&x[i],&y[i]),th[i]=h[i];
for(int t=0;t<=m;t++){
if(th[0]==a[0]&&th[1]==a[1]) return !printf("%lld\n",t);
for(int i=0;i<2;i++) th[i]=(th[i]*x[i]+y[i])%m;
}for(int i=0;i<2;i++){
memset(vs,0,sizeof(vs)),memset(t,0,sizeof(t));
int u=h[i]; while(!vs[u]) t[u]=(l[i]++),vs[u]=1,u=(x[i]*u+y[i])%m;
int va=u; u=h[i]; ls[i]=t[va];
for(int tp=0;tp<t[va];tp++) l[i]--,vs[u]=0,u=(x[i]*u+y[i])%m;
if(!vs[a[i]]) return !printf("-1"); p[i]=t[a[i]]-t[va];
}for(int i=0;i<=l[1];i++) if((l[0]*i+p[0]+ls[0]-ls[1])%l[1]==p[1])
return !printf("%lld\n",(l[0]*i+p[0]+ls[0]-ls[1]));
return !printf("-1");
}
E. Hidden Word
题意:一个 \(2\times 13\) 的矩阵,每个格子填一个字母。两个格子相邻按照八连通判定。现给定一个长度 \(27\) 的字符串,且每个字母至少出现一次,构造一个填字母的方法,使该字符串能对应矩阵中一个路径。
显然问题的关键在于那个重复的字母如何经过两次。观察样例可以发现,可以如下构造:
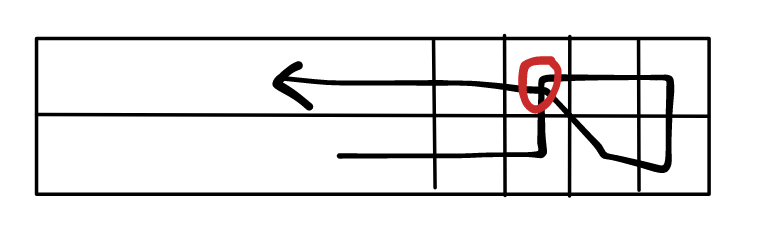
此时该字母的两次出现之间隔了偶数个字母。如果隔了奇数个,可以如下构造:

对于左边的填法,字母多的行绕到另一行补齐一下即可。
By cxm1024
#include <bits/stdc++.h>
using namespace std;
bool vis[26];
char a[2][13];
signed main() {
string s;
cin >> s;
char now = 'A', flag;
for (int i = 0; i < s.size(); i++) {
if (!vis[s[i] - 'A'])
vis[s[i] - 'A'] = s[i];
else flag = s[i];
}
vector<int> v;
for (int i = 0; i < s.size(); i++)
if (s[i] == flag) v.push_back(i);
if (v[0] + 1 == v[1]) puts("Impossible");
else {
int x = 0, y = 13 - (v[1] - v[0] - 1) / 2;
a[x][y - 1] = flag;
if (y == 13) y--, x++;
for (int j = v[0] + 1; j < v[1]; j++) {
a[x][y] = s[j];
if (x == 0) y++;
else y--;
if (y == 13) y--, x++;
}
a[0][13 - (v[1] - v[0] - 1) / 2 - 2] = flag;
x = 0, y = 13 - (v[1] - v[0] - 1) / 2 - 2;
if (y < 0) y = 0, x = 1;
for (int j = v[1] + 1; j < s.size(); j++) {
a[x][y] = s[j];
if (x == 0) y--;
else y++;
if (y < 0) x++, y = 0;
}
x = 1, y = 13 - (v[1] - v[0]) / 2 - 1;
if (y < 0) y = 0, x = 0;
for (int j = v[0] - 1; j >= 0; j--) {
a[x][y] = s[j];
if (x == 1) y--;
else y++;
if (y < 0) x--, y = 0;
}
for (int i = 0; i <= 1; i++) {
for (int j = 0; j < 13; j++)
cout << a[i][j];
cout << endl;
}
}
return 0;
}
F. Video Cards
题意:有 \(n\) 个元素,你可以选一个元素作为中心元素,其他元素中选若干个作为附属元素,要求附属元素必须为中心元素的倍数,否则可以通过减小附属元素来调整至合法。注意中心元素不能调整。求和最大的合法方案。\(n,V\le 2\times 10^5\)
容易发现附属元素必然可以全选(最差也可以减少到 \(0\)),且把中心元素当成附属元素处理也可以(自己是自己的倍数),于是问题转化为,选一个中心元素 \(x\),使得 \(\sum\limits_{i=1}^n a_i-(a_i\bmod x)\) 最大。进一步转化为最大化 \(\sum\limits_{i=1}^n \left\lfloor \frac{a_i}{x}\right\rfloor\cdot x=x\sum\limits_{i=1}^n \left\lfloor \frac{a_i}{x}\right\rfloor\)。
容易发现在 \([kx,(k+1)x)\) 内的所有元素 \(y\),\(\left\lfloor \frac{y}{x}\right\rfloor\) 的值都为 \(k\),于是对于一个 \(x\),本质不同的值最多只有 \(n/x\) 个,所以可以调和级数计算答案。预处理值域上的前缀和,复杂度 \(O(V\log(V))\)。
By cxm1024
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, a[200010], s[200010];
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
s[a[i]]++;
}
for (int i = 1; i <= 200000; i++)
s[i] += s[i - 1];
long long ans = 0;
for (int i = 1; i <= 200000; i++) {
if (s[i] - s[i - 1] == 0) continue;
long long res = 0;
for (int j = i; j <= 200000; j += i)
res += (s[min(200000ll, j + i - 1)] - s[j - 1]) * (j / i);
ans = max(ans, 1ll * i * res);
}
printf("%lld\n", ans);
return 0;
}
G. Masha-forgetful
题意:给定 \(n\) 个模式串 \(s_1\cdots s_n\) 和一个文本串 \(t\),长度均为 \(m\),字符集为 \(0\sim 9\)。定义一个 \(t\) 的子串合法,当且仅当长度 \(\ge 2\) 且在某个 \(s\) 中出现过。构造将 \(t\) 划分为合法子串的方案或判断无解。\(T\le 10^4,\sum nm\le 10^6\)
显然对于一个合法的字符串,其所有长度 \(\ge 2\) 的子串也合法。于是有一个非常重要的结论:\(t\) 的划分长度要么为 \(2\) 要么为 \(3\)。于是可以暴力预处理出模式串中出现过的所有长度为 \(2\) 或 \(3\) 的字符串,暴力 DP 即可。
By zhouhaoxu
#include<bits/stdc++.h>
#define N 200005
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
using namespace std;
int f[N],T,n,m,pr[N]; map<string,pii >st;
bool is(string s){return st.find(s)!=st.end();}
struct node{int l,r,k;}; vector<node>ans;
void calc(string u){
pii p=st[u]; ans.pb((node){p.se,p.se+(int)u.size()-1,p.fi});
}string s,t; signed main(){
ios::sync_with_stdio(false),cin>>T;
while(T--){
cin>>n>>m,st.clear(),ans.clear();
for(int i=1;i<=n;i++){
cin>>s; for(int j=0;j<m;j++){
if(j+1<m) st[s.substr(j,2)]=make_pair(i,j);
if(j+2<m) st[s.substr(j,3)]=make_pair(i,j);
}
}cin>>t; for(int i=0;i<=m;i++) f[i]=pr[i]=0;
if(m==1){cout<<-1<<endl; continue;}
if(m>1) f[1]=is(t.substr(0,2));
if(m>2) f[2]=is(t.substr(0,3));
for(int i=1;i<m;i++){
if(!f[i]) continue;
if(i+2<m&&is(t.substr(i+1,2))) f[i+2]=1,pr[i+2]=i;
if(i+3<m&&is(t.substr(i+1,3))) f[i+3]=1,pr[i+3]=i;
}if(!f[m-1]) cout<<-1<<endl; else{
int r=m-1;
while(r>2) calc(t.substr(pr[r]+1,r-pr[r])),r=pr[r];
calc(t.substr(0,r+1)); reverse(ans.begin(),ans.end());
cout<<(int)ans.size()<<endl;
for(auto &u:ans) cout<<u.l+1<<' '<<u.r+1<<' '<<u.k<<endl;
}
}return 0;
}
如果没有注意到段长必须为 2 或 3,其实也可以做。设 \(f_i\) 表示是否能将前 \(i\) 个字符划分成合法的段,则 \(f_i=f_j\vee f_{j+1}\vee\cdots\vee f_{i-1}\),其中 \(j\) 为最小的使 \(t_{[j+1,i]}\) 合法的位置。显然转移可以使用前缀和优化,所以只需要找到最小的合法的 \(j\) 即可。
要对每个位置找到最长的出现过的后缀,可以使用 SAM 维护。首先将 \(s_1\#s_2\#\cdots\#s_n\) 建 SAM,则其中维护了所有 \(s\) 的子串信息。每次尝试在当前节点添加一个字符,如果不能转移则在 parent tree 上跳 fa,直到能转移,此时即为最长后缀。
注意转移时 \(j\ne i-1\)(长度至少为 \(2\)),特殊处理一下即可。
By cxm1024
#include <bits/stdc++.h>
using namespace std;
string t;
struct node {
int fa, nxt[11], len, tag, r;
node() {
fa = len = tag = r = 0;
memset(nxt, 0, sizeof(nxt));
}
} a[2000010];
int lst = 1, cnt = 1;
void insert(int x, int y, int z) {
int p = lst, now = ++cnt;
a[now] = node();
a[now].len = a[lst].len + 1, a[now].tag = y, a[now].r = z;
for (; p && a[p].nxt[x] == 0; p = a[p].fa)
a[p].nxt[x] = now;
int q = a[p].nxt[x];
if (q == 0) a[now].fa = 1;
else if (a[p].len + 1 == a[q].len) a[now].fa = q;
else {
int r = ++cnt;
a[r] = node();
a[r] = a[q], a[r].len = a[p].len + 1;
for (; p && a[p].nxt[x] == q; p = a[p].fa)
a[p].nxt[x] = r;
a[q].fa = a[now].fa = r;
}
lst = now;
}
int f[1010], g[1010], pre[1010];
int rr[1010], ii[1010];
void Solve(int test) {
lst = cnt = 1, a[1] = node();
int n, m;
cin >> n >> m;
for (int i = 0; i <= m; i++) {
f[i] = g[i] = 0;
pre[i] = rr[i] = ii[i] = 0;
}
for (int i = 1; i <= n; i++) {
string s;
cin >> s;
for (int j = 0; j < s.size(); j++)
insert(s[j] - '0', i, j + 1);
insert(10, i, 0);
}
cin >> t;
t = " " + t;
int now = 1, l = 1;
if (a[now].nxt[t[1] - '0']) now = a[now].nxt[t[1] - '0'];
else l = 2;
for (int i = 2; i <= m; i++) {
while (now != 1 && a[now].nxt[t[i] - '0'] == 0)
l = i - a[a[now].fa].len, now = a[now].fa;
g[i] = g[i - 1];
if (a[now].nxt[t[i] - '0'] == 0) l = i + 1;
if (a[now].nxt[t[i] - '0']) {
now = a[now].nxt[t[i] - '0'];
if (l == 1) {
f[i] = 1, pre[i] = 0;
rr[i] = a[now].r, ii[i] = a[now].tag;
g[i] = i;
}
else if (g[i - 2] >= l - 1) {
f[i] = 1, pre[i] = (i == 0 ? -1 : g[i - 2]);
rr[i] = a[now].r, ii[i] = a[now].tag;
g[i] = i;
}
}
}
if (!f[m]) cout << -1 << endl;
else {
vector<array<int, 3> > ans;
int now = m;
while (now) {
ans.push_back({rr[now] - (now - pre[now]) + 1, rr[now], ii[now]});
now = pre[now];
}
reverse(ans.begin(), ans.end());
cout << ans.size() << endl;
for (auto [x, y, z] : ans)
cout << x << " " << y << " " << z << endl;
}
while (cnt) a[cnt--] = node();
for (int i = 0; i <= m; i++) {
f[i] = g[i] = 0;
pre[i] = rr[i] = ii[i] = 0;
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T;
cin >> T;
for (int _test = 1; _test <= T; _test++)
Solve(_test);
return 0;
}
H. Nearest Fraction
题意:给定一个分数 \(\frac{x}{y}\),求一个分数 \(\frac{a}{b}\) 使得 \(b\le n\),且与 \(\frac{x}{y}\) 尽可能接近。如有相同则取较小的 \(\frac{a}{b}\)。\(x,y,n\le 10^5\)
由于 \(n\) 很小,可以枚举分母。对于一个分母来说,可以通过二分答案来确定最接近的分子。在此题中 double 的精度足够通过。
By zhouhaoxu
#include<bits/stdc++.h>
#define int long long
#define N 200005
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
using namespace std;
int x,y,n,a0=-1,b0=-1; double ans=1;
signed main(){
scanf("%lld%lld%lld",&x,&y,&n);
for(int i=1;i<=n;i++){
int l=0,r=(int)1e10,ret=0; while(l<=r){
int md=(l+r)>>1; if(md*y<=i*x) ret=md,l=md+1;
else r=md-1;
}for(int j=max(ret-2,0ll);j<=ret+2;j++){
double va=fabs(1.0*x/y-1.0*j/i);
if(a0==-1){ans=va,a0=j,b0=i; continue;}
if(ans-va>1e-15) ans=va,a0=j,b0=i;
else if(fabs(ans-va)<1e-15){
if(b0>i) b0=i,a0=j; else if(b0==i) a0=min(a0,j);
}
}
}return !printf("%lld/%lld\n",a0,b0);
}
事实上,最接近的分子可以直接得出,而无需二分答案。当 \(\frac{a}{b}\approx\frac{x}{y}\) 时,有 \(a\approx\frac{bx}{y}\)。所以只需要在该值附近枚举一两个相邻元素即可。
By AmirAz
#include <iostream>
#include <cstdio>
#include <set>
#include <cmath>
using namespace std;
typedef long long ll;
bool comp(ll a, ll b, ll x1, ll y1, ll x2, ll y2){
return (abs(a * y1 * y2 - x1 * b * y2) < abs(a * y2 * y1 - x2 * b * y1));
}
int main(){
ll a, b, n; cin >> a >> b >> n;
ll minx = 1e7 + 10, miny = 1;
for (ll i = 1; i <= n; i++){
ll y = i;
ll x = floor((long double) y * a / b);
if (comp(a,b, x, y, minx, miny)){
minx = x;
miny = y;
}
x = ceil((long double)y * a / b);
if (comp(a,b, x, y, minx, miny)){
minx = x;
miny = y;
}
}
cout << minx << "/" << miny << endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号