最小生成树

最小生成树

• \(G = (V, E)\),若\(G\)的一个生成子图是一棵树，则称之为\(G\)的一棵生成树（记为T）
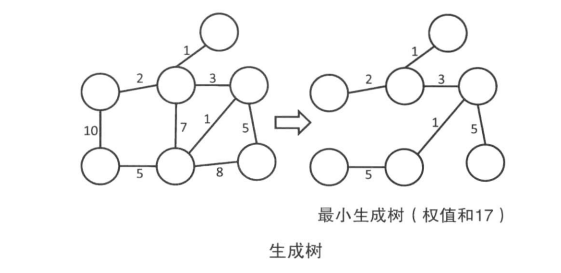
• 最小生成树：无向图\(G\)的所有生成树中，树枝的权值总和最小的称为\(G\)的最小生成树。
  
  常见的求解最小生成树的算法有\(Prim\)算法和\(Kruskal\)算法。显然，生成树是否存在和图是否连通是等价的，因此我们假设图是连通的。

最小生成树问题1（\(Prim\)算法）

最小生成树和最短路的区别

• 最小生成树： 把连通的图的所有顶点连起来路径之和最小的问题，即生成树总权值之和最小。
• 最短路： 把两点之间路径最短。
  最短路只是将两点连起来，其路径并不一定经过所有点，而最小生成树要连接每一个点。
  prim和dijkstra思路区别
  \(dijkstra\):把所有点到源点距离dis初始化为∞，每次找到dis最小的点确定下来（加入到路径中），并用该点距离更新所有点到源点距离
  dis[i]=min(dis[i],dis[ver]+w[i])
  即：用源点拓展，每次确定距离最近的点，直到终点！
  \(prim\)：把所有点到集合的距离dis初始化为∞,每次找到dis最小的点确定加来（加入到集合中），并用该点距离更新所有点到集合的距离
  dis[i]=min(dis[i],g[t][j])
  即：随意找一个起点，每次确定到集合最近的点，直到所有点都确定完！
  \(Prim\)算法和\(Dijkstra\)算法相似，都是从某个顶点出发，不断添加边的算法。
  (都需要维护一个集合S,但是这个集合的含义不同)

Prim算法求最小生成树

#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define bug(x) cout<<#x<<"=="<<x<<endl;
#define endl "\n"
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int inf = 0xc0c0c0c0;


const int N = 510, M = 2e5 + 10;
int n, m;
int g[N][N];
int dis[N];
bool st[N];

int prim() {
	memset(dis, 0x3f, sizeof dis);

	int res = 0;
	for (int i = 0; i < n; i++) {
		int t = -1;
		for (int j = 1; j <= n; j++) {
			if (!st[j] && (t == -1 || dis[t] > dis[j])) {
				t = j;
			}
		}

		if (i && dis[t] == INF) return INF;
		if (i) res += dis[t];
		st[t] = true;

		for (int j = 1; j <= n; j++) dis[j] = min(dis[j], g[t][j]);
	}

	return res;
}

int main() {
	ios;
	cin >> n >> m;
	memset(g, 0x3f, sizeof g);

	while (m--) {
		int u, v, w;
		cin >> u >> v >> w;
		g[u][v] = min(g[u][v], w);
		g[v][u] = min(g[v][u], w);
	}

	int t = prim();

	if (t == INF) cout << "impossible" << endl;
	else cout << t << endl;
	return 0;
}

最小生成树模板题（kruskal算法)
kruskal
\(kruskal\)算法思想： 贪心地选取最短的边来组成一棵最小的生成树。
具体做法： 先将所有的边的权值从小到大排序，按照边的权值的顺序从小到大查看一遍，如果不产生圈（重边等也算在内），就把当前这条边加入到生成树中。
考虑如何判断是否产生圈？
假设现在要把连接顶点\(u\)和顶点\(v\)的边\(e\)加入生成树中。如果加入之前\(u\)，\(v\)不属于同一个集合，那么加入\(e\)也不会产生圈。反之，如果\(u\)，\(v\)在同一个集合，那么一定会产生圈。所以，考虑用并查集判断是否在一个集合。

#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define bug(x) cout<<#x<<"=="<<x<<endl;
#define endl "\n"
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int inf = 0xc0c0c0c0;

/*
  kruskal算法
  贪心思想：贪心地选取最短的边来组成一棵最小的生成树
  具体做法：先将所有的边做排序，然后利用并查集作判断来优先选择较小的边，
		    直到建成一棵生成树。

  prim和kruskal的比较
  prim和kruskal的贪心策略是一样的，都是选耗费最小的边
  对于prim，定义一个集合s表示当前已经在最小生成树里面的点的集合，
  而选取的边必有一个顶点已经被覆盖，另一个顶点未被覆盖
  而对于kruskal，其选取的边任意，只要这个边的加入不能使被覆盖的顶点构成回路

  小细节：
  1.如何判断是否会产生回路：使用并查集
  init()
  遍历从小到大排序好的每条边，判断该条边两个顶点是否在一个连通块，如果在一个连通块，
  说明这两个顶点已经连通，这条边不要。如果不在一个连通块，则最小生成树要加上这条边
 */


const int N = 1e5 + 10, M = 2e5 + 10;
int n, m;
int fa[N];

//因为只需要存所有边的信息就行，所以不需要建图，只需用结构体存即可
struct Edge {
	int a, b, w;
} edges[M];

//对边排序
bool cmp(Edge a, Edge b) {
	return a.w < b.w;
}
//并查集判断是否在一个连通块
int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

int kruskal() {
	sort(edges, edges + m, cmp);

	//并查集的初始化操作
	for (int i = 1; i <= n; i++)  fa[i] = i;

	int res = 0, cnt = 0;//res:最小生成树的权值，cnt最小生成树的边数
	for (int i = 0; i < m; i++) {
		int a = edges[i].a, b = edges[i].b, w = edges[i].w;
		a = find(a), b = find(b);
		if (a != b) {
			fa[a] = b;
			res += w;
			cnt++;
		}
	}

	if (cnt < n - 1) return INF;//n-1:指n个顶点能组成最小生成树，有n-1条边。若cnt<n-1说明有顶点孤立
	return res;
}

int main() {
	ios;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> edges[i].a >> edges[i].b >> edges[i].w;
	}

	int t = kruskal();
	if (t == INF) cout << "impossible" << endl;
	else cout << t << endl;
	return 0;
}