背包问题

01背包每件物品最多只用一次
完全背包每件物品有无限个
多重背包每个物品最多有\(s_i\)个(朴素版，优化版)
分组背包，有\(n\)组，每组物品有若干种

简化的01背包

分析:

原问题:\(i\)件物品选若干件组成的小于\(V\)的最大体积是多少？
用可行性描述就可
bool数组\(f[i][j]\)表示前i个物品能否放满体积为j的背包
枚举最后一次决策——第i个物品放还是不放
\(f[i][j]=f[i-1][j]||f[i-1][j-a[i]]\)
初值 \(f[i][j]=0, f[0][0]=1\)

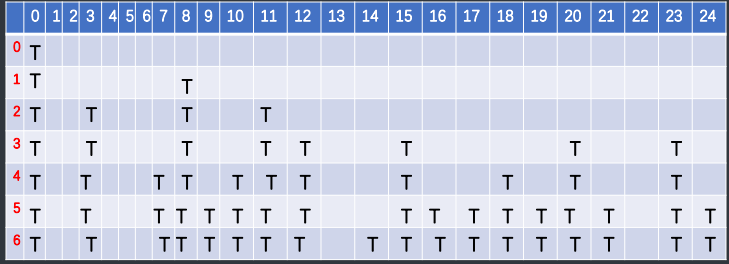
我们可以看到每一行的结果实际上只与上一行有关，所以就可以01滚动——\(f[0,1][j]\)一行记录前一行的值，另一行记录当前行的值
对于本题更加常用的方法是就地滚动
就地滚动就是用一个一维数组，之前的状态和当前的状态都记在同一个数组里了

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

int v, n;
int a[40];
int f[2][20020];

int main() {
	cin >> v >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	
	memset(f, 0, sizeof(f));
	f[0][0] = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j <= v; j++) {		//这里j要从0开始，不能从a[i]
			if (j >= a[i]) {
				f[i % 2][j] = f[(i - 1) % 2][j] || f[(i - 1) % 2][j - a[i]];//放或不放
			} else {
				f[i % 2][j] = f[(i - 1) % 2][j];	//小于就直接继承
			}
		}
	}
	
	int ans = 0;
	for(int i = v; i >= 0; i--){
		if(f[n%2][i] == 1){
			ans = i;
			break;
		}
	}
	cout << v - ans << endl;
	return 0;
}

/*
输入:24 6
     8 3 12 7 9 7
输出:0
*/

01背包

题目描述:
有\(N\)件物品和一个容量是\(V\)的背包。每件物品只能使用一次。
第i件物品的体积是\(v_i\)价值是\(w_i\)。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

分析:
动态规划是不断决策求最优解的过程,「0-1 背包」即是不断对第\(i\)
个物品的做出决策,「0-1」正好代表不选与选两种决定。

题解代码

version 1递归

最朴素的方法，针对每个物品是否放入背包进行搜索

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1010;
int n, m;
int w[N], v[N];

//从第i个物品开始挑选总量小于j的部分
int rec(int i, int j) {
	int res;

	if (i == n) {	//已经没有剩余物品
		res = 0;
	} else if (j < w[i]) {	//无法挑选这个物品
		res = rec(i + 1, j);
	} else {
		//挑选和不挑选的两种情况都尝试一下
		res = max(rec(i + 1, j), rec(i + 1, j - w[i]) + v[i]);
	}
	return res;
}


void solve() {
	printf("%d\n", rec(0, m));
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> w[i] >> v[i];
	}
	solve();
	return 0;
}

这种方法的搜索深度是\(n\),而且每一层的搜索都需要两次分支，最坏就需要\(O(2^n)\)的时间，n较大无法求解。

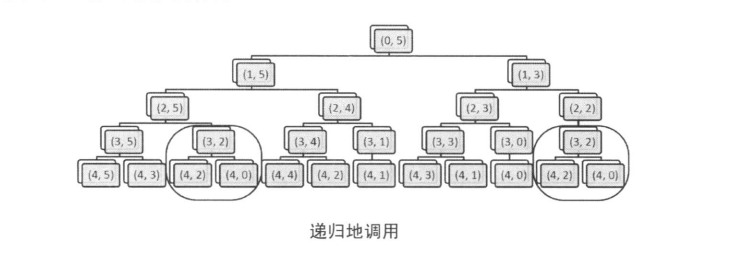
如图，rec以（3，2）为参数调用了两次。第二次调用已经知道了结果却浪费了时间。我们可以在这里把第一次计算的结果记录下来。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1010;
int n, m;
int w[N], v[N];

int dp[N][N];	//记忆化数组

//从第i个物品开始挑选总量小于j的部分
int rec(int i, int j) {
	//如果已经计算过的话直接使用之前的结果
	if (dp[i][j] >= 0) return dp[i][j];

	int res;
	if (i == n) {	//已经没有剩余物品
		res = 0;
	} else if (j < w[i]) {	//无法挑选这个物品
		res = rec(i + 1, j);
	} else {
		//挑选和不挑选的两种情况都尝试一下
		res = max(rec(i + 1, j), rec(i + 1, j - w[i]) + v[i]);
	}
	return dp[i][j] = res;
}

void solve() {
	//用-1表示尚未计算过，初始化整个数组
	memset(dp, -1, sizeof(dp));
	printf("%d\n", rec(0, m));
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> w[i] >> v[i];
	}
	solve();
	return 0;
}

这个优化对于同样的参数，只会在第一次被调用时执行递归部分，第二次之后都会直接返回。这种方法就是记忆化搜索。

version 2 二维

(1)状态f[i][j]定义前i个物品，背包容量\(j\)下的最优解(最大价值)；

当前的状态依赖于之前的状态，可以理解为从初始状态f[0][0]=0,开始决策，有\(n\)件物品，则需要\(n\)次决策，每一次对第\(i\)件物品的决策，状态f[i][j]不断由之前的状态更新而来。
(2)当前背包容量不够（j<v[i]),没得选，因此前\(i\)个物品最优解即为前\(i-1\)个物品最优解。
对应代码:f[i][j]=f[i-1][j];
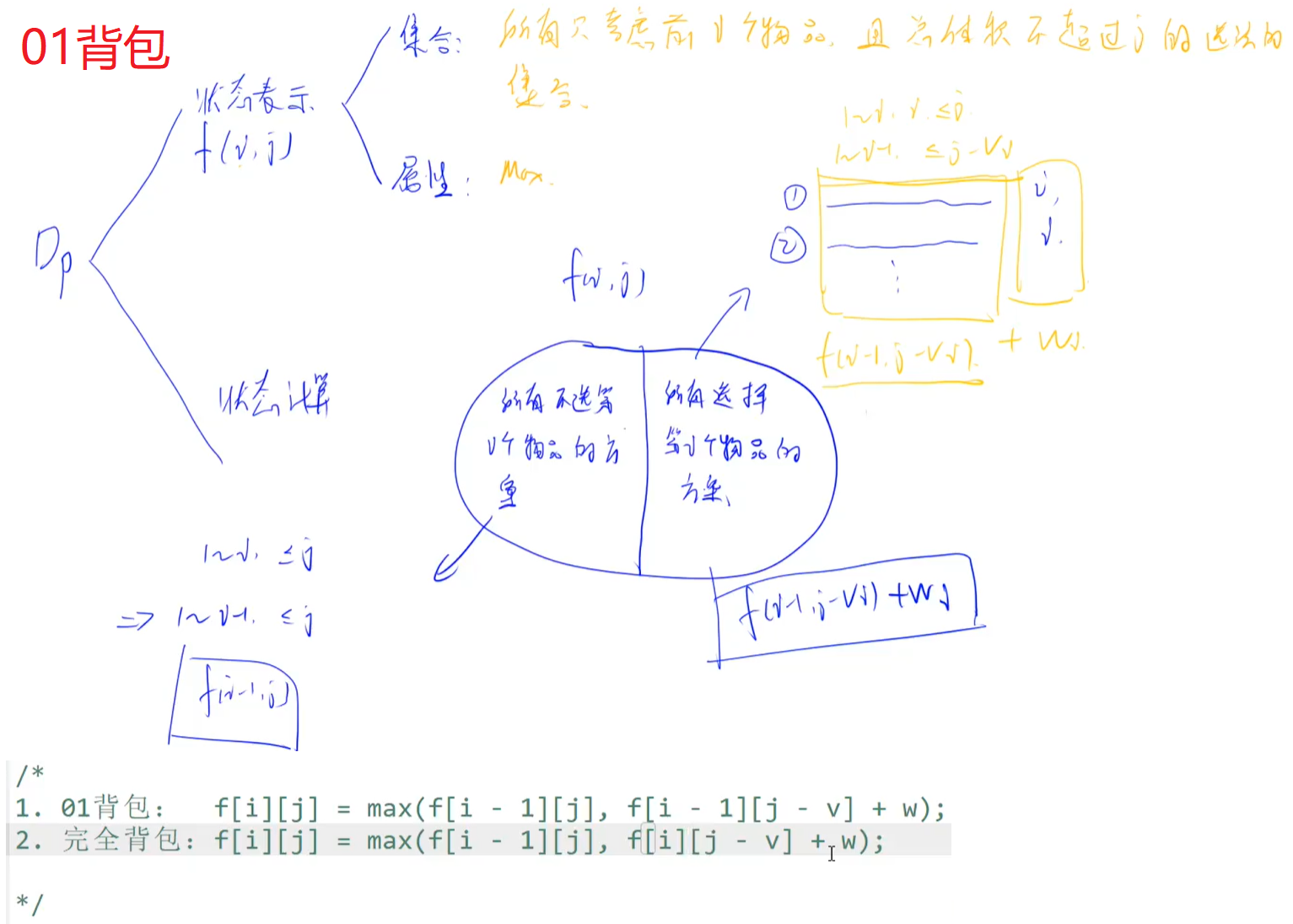
(3)当前背包容量够，可以选，因此需要决策选与不选第i个物品:
选：f[i][j]=f[i-1][j-v[i]]+w[i];
不选：f[i][j]=f[i-1][j];
我们的决策是如何取到最大价值，因此以上两种情况取max()

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> v[i] >> w[i];
	}

	for (int i = 1; i <= n; i++) {
		for (int j = 0; j <= m; j++) {//01背包 二维 正序/逆序更新都可以，完全背包二维只能正序更新
			if (j < v[i]) f[i][j] = f[i - 1][j];
			else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
			//完全背包:f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i];
		}
	}

	cout << f[n][m] << endl;
	return 0;
}

version 3 一维

将状态f[i][j]优化到一维f[j],实际上只需要做一个等价变形。
为什么可以？
我们定义的状态f[i][j]可以求得任意合法的i与j最优解，但题目只需要求得最终状态f[n][m],因此只需要一维的空间来更新状态。
（1）状态f[j]定义：N件物品，背包容量j下的最优解。
（2）注意枚举背包容量j必须从m开始。
（3）为什么一维情况下枚举背包容量需要逆序？ 在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
（4）例如，一维状态第i轮对体积为\(3\)的物品进行决策，则f[7]由f[4]更新而来，这里的f[4]正确应该是f[i - 1][4]，但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。当逆序枚举背包容量j时，我们求f[7]同样由f[4]更新，但由于是逆序，这里的f[4]还没有在第i轮计算，所以此时实际计算的f[4]仍然是f[i - 1][4]。
状态转移方程：f[j] = max(f[j], f[j-v[i]] + w[i]);
1.如果当前位置的东西不拿的话，和前一位置的信息（原来i-1数组的这个位置上的值）是相同的，所以不用改变。
2.如果当前位置的东西拿了的话，需要和前一位置的信息（原来i-1数组的这个位置上值）取max。
3.每次i++，就从后往前覆盖一遍f数组，看每个位置上的值是否更新。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

	for (int i = 1; i <= n; i++) {
		for (int j = m; j >= v[i]; j--) { //01背包 二维--> 一维后只能逆序更新
			//for(int j = 0; j <= m; j++) //01背包二维更新，正序和逆序都可以

			if (j < v[i]) f[j] = f[j];	  //j < v[i],f[j] = f[j]是恒等式可以删除
			//f[i][j] = f[i-1][j];		  //01背包（二维）
			else f[j] = max(f[j], f[j - v[i]] + w[i]);
			// 01背包(二维)：  f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
			// 完全背包(二维)：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
		}
	}

	cout << f[m] << endl;	//f[n][m] --> f[m]
	return 0;
}

实际上，只有当枚举的背包容量>= v[i]时才会更新状态，因此我们可以修改循环终止条件进一步优化。

关于状态f[j]的补充说明
二维下的状态定义是前\(i\)件物品，背包容量\(j\)下的最大价值，一维下，少了前\(i\)件物品这个维度，我们的代码中决策到第\(i\)件物品（循环到第\(i\)轮），f[j]就是前i轮已经决策的物品背包容量\(j\)下的最大价值。
因此当执行完循环结构后，由于已经决策了所有物品，f[j]就是所有物品背包容量\(j\)下的最大价值。即一维f[j]等价于二维f[n][j];

完全背包

朴素算法（数据加强，已tle)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e3 + 10;
int n, m;
int v[N], w[N];
int f[N][N];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> v[i] >> w[i];
	}

	for (int i = 1; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			for (int k = 0; k * v[i] <= j; k++) {
				f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
			}
		}
	}

	cout << f[n][m] << endl;
	return 0;
}

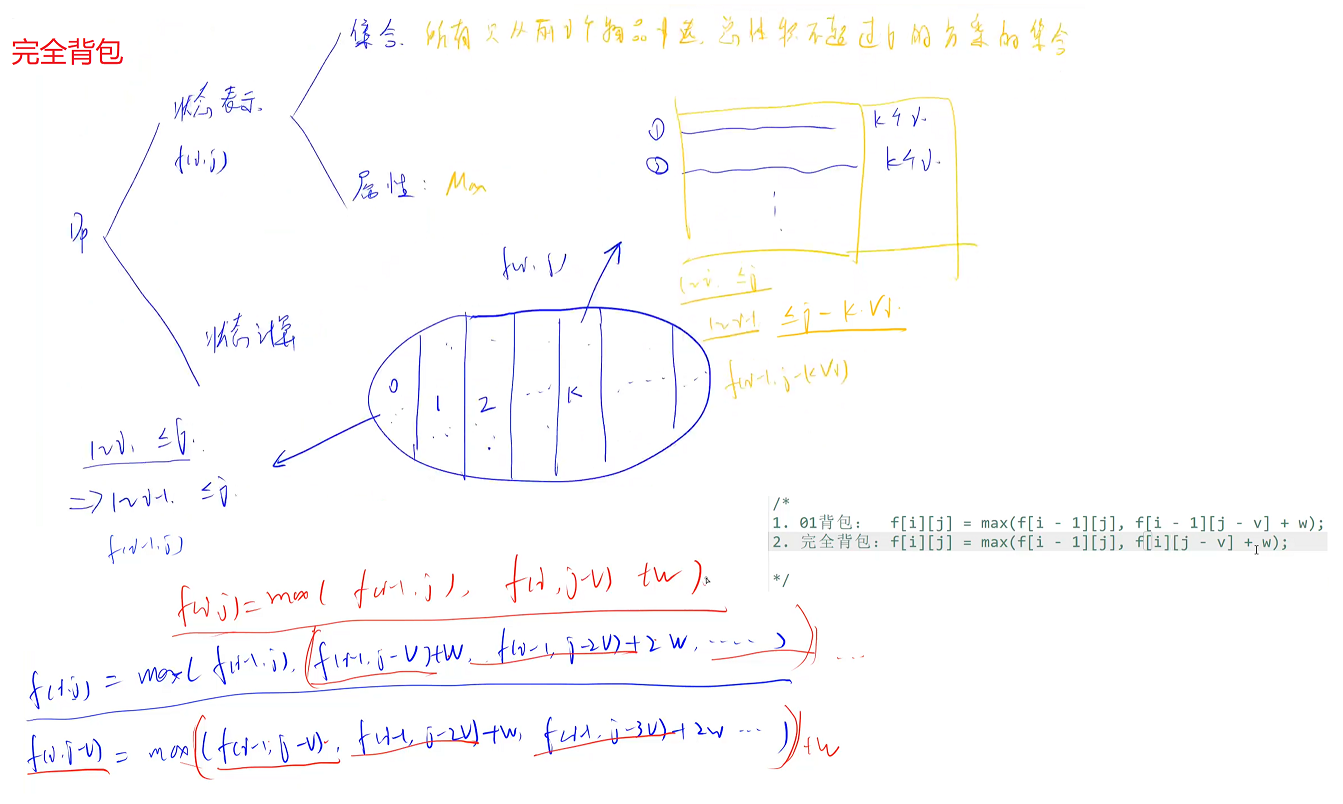
实际上，我们在计算状态方程时不必多一个循环去单独枚举选择第\(i\)个物品个数。
二维朴素写法

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {

	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			f[i][j] = f[i - 1][j];
			if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
		}
	}
	cout << f[n][m] << endl;
	return 0;
}

// 完全背包：二维朴素写法
#include<bits/stdc++.h>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ ){ // 完全背包 二维 只能 正序更新, 01背包 二维 正序/逆序 更新 都可以
        // for (int j = m; j >= 0; j -- ){ // 完全背包 二维 逆序更新 会报错

            if (j < v[i]) f[i][j] = f[i - 1][j];
            else f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
            // 01 背包：f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;
    return 0;
}

完全背包二维之所以只能正序更新，不能逆序更新是因为：f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);想求f[i][j-v[i]],两者都是f[i],也就是在同一层，所以只能正序更新。
01背包二维之所以正序逆序都可以是因为：f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);想求f[i][j],要先求f[i-1][j-v[i]],前者是f[i],后者是f[i-1],不在同一层，所以正序逆序更新都可以。
优化空间到一维

// 完全背包：二维朴素写法 ---> 一维空间优化写法 过程展示：
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ ){ // 完全背包 一维 只能 正序更新
        // 01背包 一维 只能 逆序更新: for (int j = m; j >= v[i]; j -- )

            if (j < v[i]) f[j] = f[j];
            // 完全背包(二维)：f[i][j] = f[i - 1][j];

            else f[j] = max(f[j], f[j - v[i]] + w[i]);
            // 完全背包(二维)：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
            // 01 背包(二维)： f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[m] << endl; // f[n][m] ---> f[m]
    return 0;
}

完全背包：二维朴素写法 —> 一维空间优化写法

完全背包：一维空间优化写法, 将以上代码最终简写为如下：（注意 for (int j = v[i]; j <= m; j ++ ) 中j 初始化为 v[j]，简化之前 j 初始化为 0）

// 完全背包：一维空间优化写法, 将 以上代码 最终简写为如下：
// 注意 for (int j = v[i]; j <= m; j ++ ) 中 j 初始化为 v[j]，简化之前 j 初始化为 0
#include<iostream>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = v[i]; j <= m; j ++ ) // 完全背包 一维 只能 正序更新
        // 01背包 一维 只能 逆序更新: for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl; // f[n][m] ---> f[m]
    return 0;
}

多重背包问题1

朴素写法

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> v[i] >> w[i] >> s[i];
	}

	for (int i = 1; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			for (int k = 0; k <= s[i] && k * v[i] <= j; k++) {
				f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
			}
		}
	}

	cout << f[n][m] << endl;
	return 0;
}

二进制优化写法

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 25000, M = 2010;

int n, m;
int v[N], w[N];//逐一枚举最大是N*logS
int f[N];	//体积< M

int main() {
	cin >> n >> m;

	int cnt = 0;//分组的组别
	for (int i = 1; i <= n; i++) {
		int a, b, s;
		cin >> a >> b >> s;
		int k = 1;//组别里面的个数
		while (k <= s) {
			cnt++;//组别先增加
			v[cnt] = a * k;//整体体积
			w[cnt] = b * k;//整体价值
			s -= k;//s要减小
			k *= 2;//组别里的个数增加
		}
		//剩余的一组
		if (s > 0) {
			cnt++;
			v[cnt] = a * s;
			w[cnt] = b * s;
		}
	}

	n = cnt;//枚举次数正式由个数变成组别数
	//01背包一维优化
	for (int i = 1; i <= n; i++) {
		for (int j = m; j >= v[i]; j--) {
			f[j] = max(f[j], f[j - v[i]] + w[i]);
		}
	}

	cout << f[m] << endl;
	return 0;
}

佬的题解

https://www.acwing.com/problem/content/discussion/content/2807/
多重背包二进制优化题解

posted @ 2023-01-30 12:54 csai_H 阅读(62) 评论(0) 收藏举报

刷新页面返回顶部

csai_H

背包问题

背包问题

简化的01背包

01背包

题解代码

version 1递归

version 2 二维

version 3 一维

完全背包

完全背包：二维朴素写法 —> 一维空间优化写法

多重背包问题1

佬的题解

公告