动态规划(一)
引入:斐波那契数列
递归版本:(太慢需要优化)
int f(int n) {
if (n == 0 || n == 1) return 1;
else return f(n - 1) + f(n - 2);
}
递推版本:
a[0] = a[1] = 1;
for (int i = 2; i <= n; i++) {
a[i] = a[i - 1] + a[i - 2];
}
return a[n];
总结: 递归重复计算了一些东西\((\)例如算\(f[6]\)时算了\(f[4]\),算\(f[5]\)时又算了\(f[4])\),重复子问题,导致算法效率低下。
解决方法:
- 空间换时间
- 已经计算过的记录下来避免重复计算
记忆化搜索版本:
int calc(int n) {
if (f[n] != 0) return f[n];
else return (f[n] = calc(n - 1) + calc(n - 2));
}
记忆化搜索
- 用数组等将已经算过的东西记录下来在下一次要使用的直接用已经算出的值,避免重复运算,去掉的重复的搜索树。
走楼梯问题
题目描述:
爬n阶的楼梯,一次可以爬1阶或2阶,问要爬完这n阶楼梯,共有多少种方法?
思考:
假设现在在第n阶楼梯上,显然上一步是在n-1阶或者n-2阶,根据分类加法原理知道,第n阶的方法=n-1阶的方法+n-2阶的方法
同样的,对于n-1阶和n-2阶用类似方法求解。
求到第1阶和第2阶时,显然方法数分别为1,2。
所以用\(f[i]\)表示爬到第i阶的方法数,那么
f[1] = 1, f[2] = 2;
f[i] = f[i-1]+f[i-2];
拓展:
若规定有\(m\)个第\(x_i\)级楼梯不能走。
解决方法:f[\(x_i\)] = 0,就相当于不能走。
爬蜂房(斐波那契变形)
题目描述:
一只蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行。计算蜜蜂从蜂房a爬到蜂房b的可能路线数。

方法:
用f[i]表示从a爬到i的方案数
\(i < a,f[i] = 0;\)
\(i = a,f[i] = 1;\)
\(i > a,f[i] = f[i-1]+f[i-2];\)
迷宫路径数
题目描述:
- 设有一个n * m的迷宫,即n行m列的迷宫。迷宫格子种分别放有0和1,1表示可通,0表示不能,从某点开始,有上下左右四个方向可走,输入起点终点坐标,问能否走出去,最少的步数是多少,有多少条路可以最快走出去。
![image]()
第一遍广搜完再来一遍,算沿着最短路的方案数。
![image]()
数字三角形
题目描述:
有一个由非负整数组成的三角形,第一行只有一个数,除了最下行之外,每个数的左下方和右下方各有一个数。从第一行的数开始,每次可以往左下或右下走一格,直到走到最下行,把沿途经过的数全部加起来,如何走才能使得这个和尽量大?
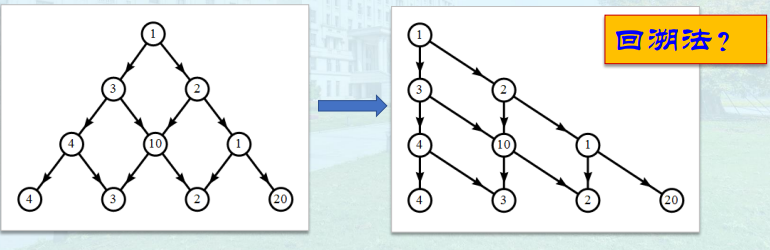
怎么存?
往左推,然后就往下走\((i+1,j)\),或往右下走\((i+1,j+1)\)
问题分析:
位置(i,j)看成一个状态,定义状态(i,j)的函数f[i][j]为:从格子(i,j)出发时能得到的最大和,则原问题的解为f[1][1]
考虑状态之间的转移(注意从有关联的状态考虑),则有f[i][j]=a[i][j]+max(f[i+1][j],f[i+1][j+1]);
怎么求f[i][j]
直接递归计算状态转移方程,效率低下
//递归计算
int f(int i, int j) {
if (i == n) return a[i][j];
int s = d[i + 1][j];
int t = d[i + 1][j + 1];
return a[i][j] + (s > t ? s : t);
}
//记忆化搜索
int f(int i, int j) {
if (dd[i][j] == -1) {
if (dd[i + 1][j] == -1) dd[i + 1][j] = d[i + 1][j];
if (dd[i + 1][j + 1] == -1) dd[i + 1][j + 1] = d[i + 1][j + 1];
dd[i][j] = a[i][j] + (dd[i + 1][j] > dd[i + 1][j + 1] ? dd[i + 1][j] : dd[i + 1][j + 1]);
}
return dd[i][j];
}
方法:
定义 f[i][j] 表示从起点走到(i,j)这个点总数 是多少
f[i][j]=a[i][j]+max(f[i-1][j],f[i-1][j-1]);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
f[i][j] = max(f[i - 1][j], f[i - 1][j - 1]) + a[i][j];
}
}
再对最后一行的f值进行扫描,最大的那一个即是结果。
动态规划原理
- 分类加法原理
- 分步乘法原理
一、动态规划若干概念
-
动态规划是解决多阶段决策过程最优化的一种方法。
-
阶段:
- 把问题分成几个相互联系的有顺序的几个环节,这些环节称为阶段。
-
状态:
- 某一阶段的出发位置称为状态。通常一个阶段包含若干状态
-
决策
- 从某阶段的一个状态演变到下一个阶段某状态的选择
-
策略
- 由开始到终点的全过程中,由每段决策组成的决策序列称为全过程的策略。
-
状态转移方程
- 前一阶段的终点就是后一阶段的起点,前一阶段的决策选择导出了后一阶段的状态,这种关系描述了由\(i\)阶段到\(i+1\)阶段状态的演变规律,称为状态转移方程。
动态规划适用的基本条件
具有相同子问题
- 首先,必须保证这个问题能够分解出几个子问题,并且能够通过这些子问题来解决这个问题
- 其次,将这些子问题作为一个新的问题,它也能分解成相同的子问题进行求解
- 假设一个问题被分解为了A,B,C三个部分,那么这A,B,C分别也能被分解为A',B',C'三个部分,而不能是D,E,F。
满足最优子结构
- 问题的最优解包含着它的子问题的最优解。即不管全面的决策如何,此后的决策必须是基于当前状态(由上一次决策产生)的最优决策。
满足无后效性
- 动态规划只适用于解决当前决策与过去状态无关的问题。状态出现在策略任何一个位置,它的地位相同,都可实施同样策略。如果当前问题的具体决策,会对解决其他为了的问题产生影响,如果产生影响,就无法保证决策的最优性。
反例:
题目描述:
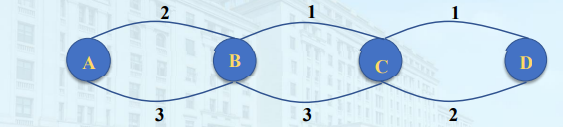
给出一个图,相邻两点之间由路径长度,求从起点到终点的路径长度对k求余的最小值,如下图,结点A到结点D路径对4求余最小值为0
![image]()
分析:设d[i]表示走到点\(i\)时,该路径\(mod k\)的最小值,状态转移方程定义为:d[i]=min{d[j]+a[i][j] mod k},其中点\(j\)到点\(i\)有道路。
\(d[A] = 0,d[B] = 2,d[C] = 1,d[D] = 2;\)
显然答案错误
原因是状态转移方程得出的阶段最优值,并不能决定下一个阶段最优值的发展,这种状态的描述不具有最优性原理。
做动态规划的一般步骤
结合原问题和子问题确定状态:
- 题目在求什么?要求出这个值我们需要知道什么?什么是影响答案的因素?
- 一维描述不完就二维,二维不行三维思维
- 状态的参数一般有:
- 描述位置的:前(后)i单位,第i到第j单位,坐标为(i,j),第i个之前(后)且必须取第i个等
- 描述数量的:取i个,不超过i个,至少i个等
- 描述对后有影响的:状态压缩的,一些特殊的性质
确定转移方程
- 检查参数是否足够
- 分情况,最后一次操作的方式,取不取,怎样去——前一项是什么
- 初始边界是什么
- 注意无后效性
- 根据状态枚举最后一次决策(即当前状态怎么开的),就可确定出状态转移方程
考虑需不需要优化
确定代码实现方式
- 递推
- 记忆化搜索
路径条数问题
题目描述:
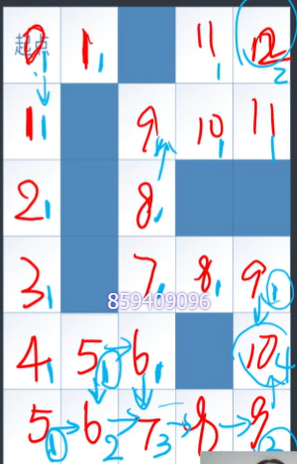
N * M的棋盘上左上角有一个过河卒,需要走到右下角。行走的规则:可以向下。或者向右。现在要求你计算出从左上角能够到达右下角的路径的条数。
状态方程
f[i][j]表示从(0,0)出发到(i,j)的路径条数。
f[i][j]=f[i-1][j]+f[i][j-1];
边界都置为1
//记忆化搜索
int calc(int i, int j){
if(f[i][j] != 0) return f[i][j];
if(i == 1 || j == 1) return f[i][j] = 1;
return f[i][j] = calc[i][j-1]+calc[i-1][j];
}
传球游戏
思路:
- 确定状态——原问题是什么?子问题是什么?
- 原问题:从1开始传球第m次传球回到1的方案数
- 子问题从1开始传球第i次到达j的方案数
- f[i][j]表示第i次传球,球在第j个人手里的方案数
- 确定状态转移方程和边界
- f[i][j]=f[i-1][j-1]+f[i-1][j-1]
- f[0][1]=1
- 注意由于是一个环,j=1时左边(j-1)为n,右边(j+1)为1
- 考虑是否需要优化
- 确定实现方法
f[i][j]表示第i次传球,球在第j个人手里的方案数
f[i][j] = f[i-1][j-1]+f[i-1][j+1];
if(j==n) j+1=1;
if(j==1) j-1=n;
边界条件
f[0][1] = 1;//第0次传球,球就在小蛮(1)手里
最长不下降子序列(LIS, Longeset Increasing Subsequence)
题目描述:
有一个长为n的数列\(a_0,a_1,a_2...a_{n-1}\),请求出这个序列中最长的不下降(上升)子序列的长度。上升子序列指的是对于任意的\(i < j\)都满足\(a_i < a_j\)的子序列。
分析:
- 确定状态——原问题?子问题?
- f[i]表示前i个数的最长不下降子序列——求不了,为什么?
- 不知道这个序列最后一个元素是哪个,没法转移
- f[i]表示以第i个数结尾的最长不下降子序列
- 确定状态转移方程
f[i]=max(f[j]+1)(a[j]<=a[i] && j<i)
f[i]=1; - 考虑是否需要优化
- O(n^2)
- 可以使用单调队列或者线段树等数据结构优化到O(nlogn)
- 确定实现方法
#include<bits/stdc++.h>
//#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
typedef long long LL;
const int N = 1e3 + 10;
int n;
int a[N];
int dp[N]; //dp数组
void solve() {
int res = 0;
for (int i = 0; i < n; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (a[j] < a[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
res = max(res, dp[i]);
}
cout << res << endl;
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
solve();
return 0;
}
/*
输入:
5
4 2 3 1 5
输出:
3
*/
//记忆化搜索
int calc(int x) {
if (f[x] != 0) return f[x];
f[x] = 1;
for (int i = 0; i < x; i++) {
if (a[i] <= a[x]) {
t = calc(i);
if (t + 1 > f[x]) {
f[x] = t + 1;
}
}
}
return f[x];
}
再想想
前面利用DP求取针对最末位的元素的最长的子序列。如果子序列的长度相同,那么最末位的元素较小的在之后会更加有优势,所以我们再反过来用DP针对相同长度情况下最小的末尾元素进行求解。
dp[i]:=长度为i+1的上升子序列中末尾元素的最小值(不存在的话就是INF)
最大子串和
题目描述:
链接:
给你一个数组 a ,包含n 个整数,你需要在其中选择连续的几个(至少一个)数,使得它们的和最大,求出最大的和。
分析
dp[i]:一定要选第i个数的情况下前i个数的最大子串和
dp[i]=max(dp[i-1]+a[i],a[i]);
#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int n;
LL a[N];
LL dp[N]; //dp数组
void solve() {
LL ans = 0;
for (int i = 1; i <= n; i++) {
dp[i] = 1;
dp[i] = max(dp[i - 1] + a[i], a[i]);
ans = max(ans, dp[i]);
}
cout << ans << "\n";
}
int main() {
ios;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
solve();
return 0;
}
/*
输入:
6
-5 6 -1 5 4 -7
输出:
14
*/
最长公共子序列(LCS Longest Common Subsequence)
题目描述:
给定两个字符串\(s_1s_2...s_n\)和\(t_1t_2...t_n\)。求出这两个字符串最长的公共子序列的长度。(1$\leq n \leq$1000)
分析:
定义: \(dp[i][j]\) = \(s_1...s_i\)和\(t_1...t_j\)对应的LCS的长度。
由此,\(s_1...s_{i+1}\)和\(t_1...t_{j+1}\)对应的公共子序列可能是
- 当\(s_{i+1}=t_{j+1}\)时,在\(s_1..s_i\)和\(t_1...t_j\)的公共子序列末尾追加上\(s_{i+1}\);
- \(s_1...s_i\)和\(t_1...t_{j+1}\)的公共子序列;
- \(s_1...s_{i+1}\)和\(t_1...t_j\)的公共子序列;
三者中的某一个,所以就有如下递推关系成立。
\(dp[i+1][j+1]\)=\(\begin{cases} max(dp[i][j]+1,dp[i][j+1],dp[i+1][j]) \ (s_{i+1}=t_{j+1})\\max(dp[i][j+1],dp[i+1][j]) \ (其他)\end{cases}\)
这个递推式可用O(nm)计算出来,\(dp[n][m]\)就是LCS的长度。
#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
typedef long long LL;
const int N = 5010;
int dp[N][N];
string a, b;
int main() {
ios;
while (cin >> a >> b) {
int n = a.size(), m = b.size();
for (int i = 1; i < n; i ++ ) {
memset(dp[i], 0, sizeof dp[i]);
}
for (int i = 0; i < n; i ++ ) {
for (int t = 0; t < m; t ++ ) {
if (a[i] == b[t]) {
dp[i + 1][t + 1] = dp[i][t] + 1;
} else {
dp[i + 1][t + 1] = max(dp[i][t + 1], dp[i + 1][t]);
}
}
}
printf("%d\n", dp[n][m]);
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号