双指针算法

双指针算法

大致格式如下：

for(int i = 0; i < n; i++){
	while(j < i && check(i, j)) j++;
	
	//每道题目的具体逻辑 
}

核心思想：

for(int i = 0; i < n; i++){
	for(int j = 0; j < n; j++){
		//O(n^2)的复杂度		
	}
}
将上述朴素算法优化到O(n)； 

例题（一）：

输入一个字符串，把其中的每一个单词输出出来。
输入：abc def ghi
输出：
abc
def
ghi

#include <bits/stdc++.h>

using namespace std;

int main(){
	char str[1000];
	
	gets(str);
	int len = strlen(str);
	for(int i = 0; i < len; i++){
		int j = i;
		while(j < len && str[j] != ' ') j++;
		
		//这道题的具体逻辑
		for(int k = i; k < j; k++){
			cout << str[k];
		} 
		cout << endl;
		i = j;
		
	}
	
	return 0;
}

例题（二）

最长连续不重复子串

核心思路：*

1. 遍历数组a中的每一个元素a[i], 对于每一个i，找到j使得双指针[j, i]维护的是以a[i]结尾的最长连续不重复子序列，长度为i - j + 1, 将这一长度与ans的较大者更新给ans。
2. 对于每一个i，如何确定j的位置：由于[j, i - 1]是前一步得到的最长连续不重复子序列，所以如果[j, i]中有重复元素，一定是a[i]，因此右移j直到a[i]不重复为止（由于[j, i - 1]已经是前一步的最优解，此时j只可能右移以剔除重复元素a[i]，不可能左移增加元素，因此，j具有“单调性”、本题可用双指针降低复杂度）。
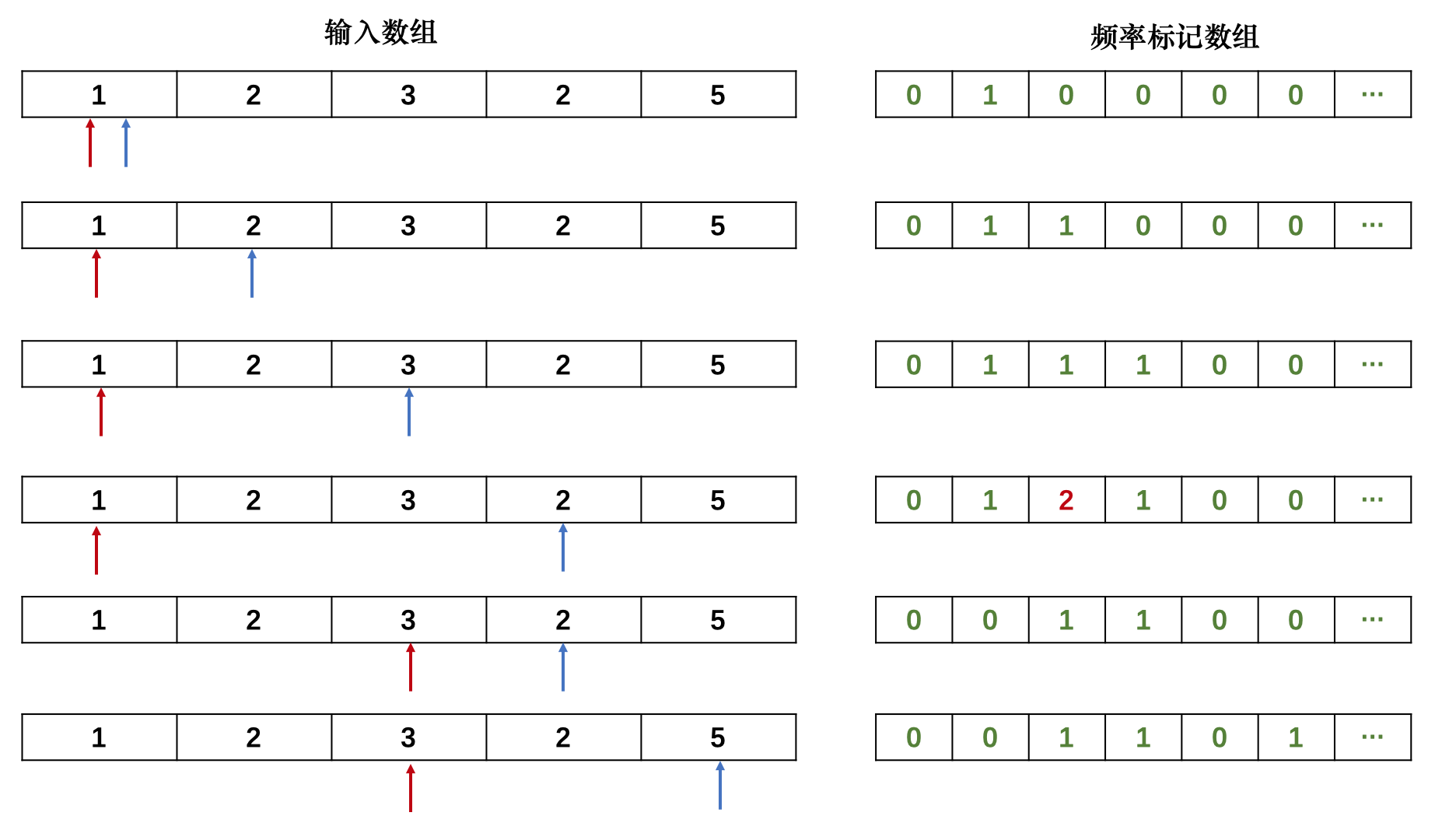
3. 用数组cnt[]记录子序列a[j ~ i]中各元素出现次数，遍历过程中对于每一个i有四步操作：cin元素a[i] -> 将a[i]出现次数cnt[a[i]]加1 -> 若a[i]重复则右移j（cnt[a[j]]要减1） -> 确定j及更新当前长度i - j + 1给ans。

代码实现：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;
int a[N], cnt[N];  //cnt[]频率标记数组

int main(){
	int n;
	cin >> n;
	for(int i = 0; i < n; i++){
		cin >> a[i];
	}
	
	int ans = 0;
	for(int i = 0, j = 0; i < n; i++){
		cnt[a[i]] ++;
		while(cnt[a[i]] > 1){   //只要a[i]的次数大于1
			cnt[a[j]] --;   //先减次数
			j++;            //再右移
		}
		ans = max(ans, i - j + 1 );  //更新答案
	}
	cout << ans << endl;

	return 0;
}

图解如下：
蓝指针为i，红指针为j;

例题（三）

数组元素的目标和
题目关键:
数组是按升序排列的
(双指针) O(n)
i从 0开始 从前往后遍历
j从 m - 1开始 从后向前遍历
和纯暴力的O(n^2) 算法的区别就在于：j指针不会回退

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;
long long a[N], b[N];

int main(){
	int n, m, x;
	cin >> n >> m >> x;
	
	for(int i = 0; i < n; i++) cin >> a[i];
	for(int i = 0; i < m; i++) cin >> b[i];

	for(int i = 0, j = m - 1; i < n; i++){
		while(j >= 0 && a[i] + b[j] > x) j--;
		if(j >= 0 && a[i] + b[j] == x) cout << i << ' ' << j << endl;
	}	
	return 0;
}

div.3 C. Traffic Light(双指针)

思路：
我们需要维护的序列是：每一个颜色\(c\)到离它最近的绿灯的距离。找到这类序列的最大距离。同时，注意红绿灯的状态是周期性的。
如何处理周期性？
我们要维护的序列一定可以在两个周期内找到\(ans\),所以可以把字符串复制一次，这样就很好地处理了红绿灯周期性的问题。
为了避免数组越界的问题，可以倒着找，从后往前找，找到绿灯就记录一下位置，如果遇到颜色\(c\)，就更新答案\(ans=max(ans, last - i)\),\(last\)是绿灯出现在颜色\(c\)之前最近的一次，\(i\)是当前时间。

#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define bug(x) cout<<#x<<"=="<<x<<endl;
#define endl "\n"
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int inf = 0xc0c0c0c0;


void solve() {
	int n;
	char c;
	cin >> n >> c;
	string s;
	cin >> s;
	s = s + s;
	int last = 0;
	int ans = inf;
	for (int i = s.size(); i >= 0; i--) {
		if (s[i] == 'g') {
			last = i;
		}
		if (s[i] == c) {
			int len = last - i;
			ans = max(ans, len);
		}
	}

	cout << ans << endl;
}

int main() {
	ios;
	int t;
	cin >> t;
	while (t--) {
		solve();
	}
	return 0;
}

总结：

常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作