二维差分矩阵

二维差分

始终记住对b[i][j]修改会影响a数组中从a[i][j]及往后的每一个数。
a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组
考虑如何构造差分数组b[i][j],使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

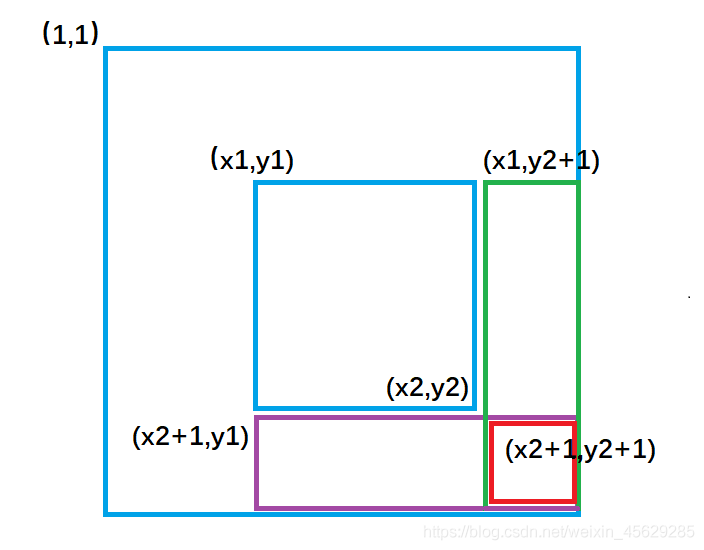
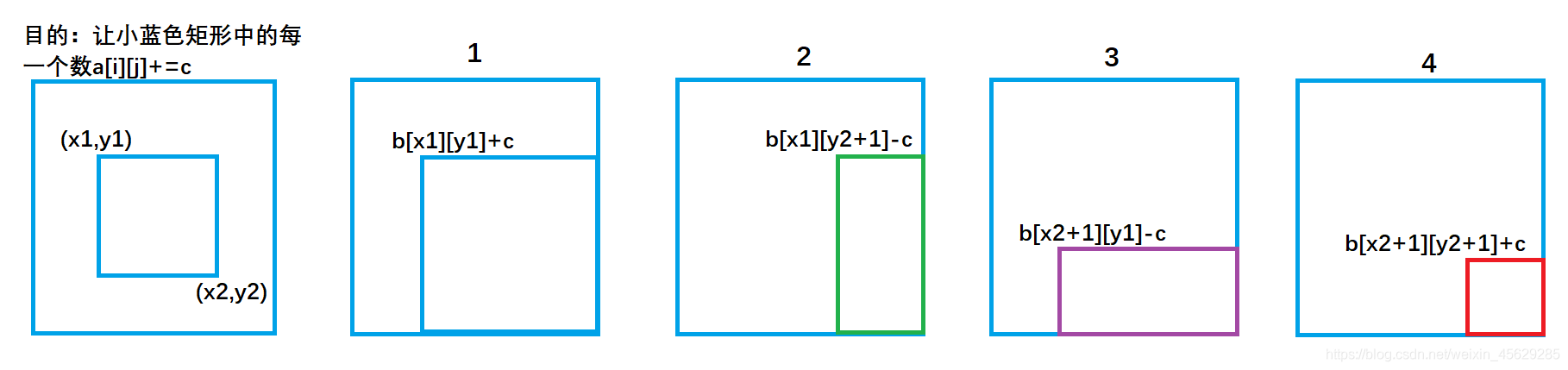
b[x1][y1] += c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1][y2+1] -= c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y1] -= c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y2+1] += c; 对应图4,,让整个a数组中红色矩形面积的元素再加上c，红色内的相当于被减了两次，再加上一次c，才能使其恢复。

上述操作被封装成insert函数

我们可以先假想a数组为空，那么b数组一开始也为空，但是实际上a数组并不为空，因此我们每次让以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j]，等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作，就成功构建了差分b数组

代码如下：

#include <bits/stdc++.h>

using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];  //b[][]是a[][]的差分数组

void insert(int x1, int y1, int x2, int y2, int c){
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}

int main(){
	int n, m, q;
	cin >> n >> m >> q;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cin >> a[i][j];
		}
	}
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j<= m; j++){
			insert(i, j, i, j, a[i][j]);  //构造差分矩阵
		}
	}
	
	while(q--){
		int x1, y1, x2, y2, c;
		cin >> x1 >> y1 >> x2 >> y2 >> c;
		insert(x1, y1, x2, y2, c); 
	}
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
		}
	}

	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			printf("%d ", b[i][j]);
		}
		printf("\n");
	}
	
	
	return 0;
}