算法基础：子矩阵的和（二维前缀和）

算法：子矩阵的和

核心公式：
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

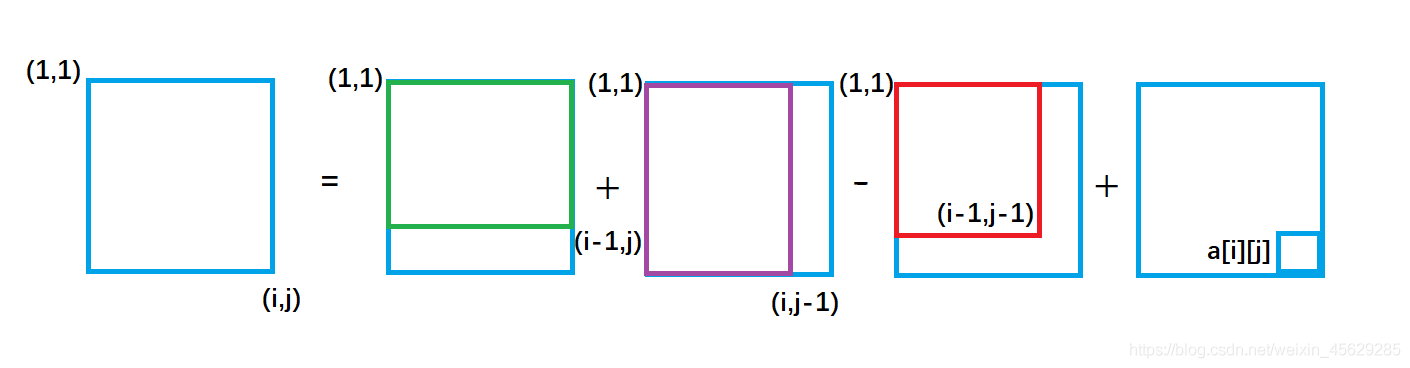
由图得，蓝色面积s[i][j]=绿色面积s[i-1][j]+紫色面积s[i][j-1]-重复加的红色面积s[i-1][j-1]+小方块面积a[i][j];
因此二维前缀和预处理公式：
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
 
#include <bits/stdc++.h>
 
using namespace std;
 
const int N = 1e3 + 10;
int a[N][N], s[N][N];  //s[n][n]二维矩阵前缀和
 
int main(){
	int n, m, q;
	cin >> n >> m >> q;
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cin >> a[i][j];
		}
	}
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]; //二维矩阵前缀和的预处理公式
		}
	}
	
	while(q--){
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;
		
		cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 -1][y2] + s[x1 -1][y1-1] << endl; 
	}
	
	
	return 0;
}
 

二维前缀和练习：
https://codeforces.com/contest/1722/problem/E

!太牛了这个思路，想不到呜呜呜！

#include <bits/stdc++.h>
 
using namespace std;
 
const int N = 1e3 + 10;
long long a[N][N], s[N][N];
 
void slove(){
	long long n, q;
	cin >> n >> q;
	
	for(int i = 0; i <= 1008; i++){		//多测清空 
		for(int j = 0; j <= 1008; j++){
			a[i][j] = 0;
			s[i][j] = 0;
		}
	}
	
	
	for(int i = 0; i < n; i++){
		int h, w;
		cin >> h >> w;
		a[h][w] += h * w;		//tql这个操作
	}
	
	for(int i = 1; i <= 1008; i++){
		for(int j = 1; j <= 1008; j++){
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];	//前缀和公式预处理 
		}
	}
 
	while(q--){
		int hs, ws, hb, wb;
		cin >> hs >> ws >> hb >> wb;
 
	/*
	
	S[i, j] = 第i行j列格子左上部分所有元素的和 
	?(x1, y1)为左上角,(x2, y2)为右小角的子矩阵的和为： 
	S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
	
	*/
 
		cout << s[hb - 1][wb - 1] - s[hs][wb - 1] - s[hb - 1][ws] + s[hs][ws] << endl;
		
	}
}
 
 
int main(){
	int t;
	cin >> t;
	
	while(t--){
		slove();
	}
 
	return 0;
}