CSP-S模拟31
T1:远征(expedition)
思路:
显然,\(1≤q≤10^6\) 根本没有给我们多少操作的空间,因此我们只能考虑初始化出一些东西,然后在查询的时候直接使用。
每次查询输入值有三个 \(l,r,x\) ,它们的数据范围为 \(1 ≤ l ≤ r ≤ 5*10^4 , 1 ≤ x ≤ 1023\) 显然直接处理三个值很容易爆,那么我们就需要舍弃其中一个值。由题面可得,我们是从先往后能杀就杀,因此 \(r\) 的作用没有 \(l\) 大,那么我们就舍弃 \(r\) ,只预处理与 \(l,x\) 有关的值。
因此,我们设 \(f_{i,j}\) 表示从 \(i\) 开始,以 \(j\) 的战斗力最先杀怪的位置在哪。这里的时间复杂度是 \(O(nV)\) 的,可以接受。
再来考虑查询部分,我们只需要暴力地从前往后找到要打的每一个怪即可。
代码:
$code$
#include<iostream>
#define int long long
using namespace std;
const int N=5e4+5;
int n,q,l,r,x,a[N],b[N],f[N][1030],ans;
signed main(){
// freopen("expedition.in","r",stdin);
// freopen("expedition.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<1024;i++){
int t=n+1;
for(int j=n;j>=1;j--){
if((a[j]|i)==i) t=j;
f[j][i]=t;
}
}
cin>>q;
while(q--){
int res=0;
cin>>l>>r>>x;
while(x){
if(f[l][x]>r) break;
res+=b[f[l][x]];
l=f[l][x];
x-=a[l];
}ans^=res;
}cout<<ans<<'\n';
return 0;
}
T2:传送(teleport)
思路:
先从最简单的开始,首先 \(0\) 和 \(-1\) 的特判应该不难吧。当 \(s=t\) 时输出 \(0\) 。当 \(s\) 与 \(t\) 所处的连通块不同时输出 \(-1\) 。
然后我们分析题目给出的 \(G'\) 图有什么作用。感觉初步判断是每当有一条长度为三的链,就给第一个和第三个之间连一条边。这有什么作用呢?
我们再来看一下样例及大样例,不难发现里面只有 \(1\) 和 \(2\) ( 当然还有我们已经特判好的 \(0\) 和 \(-1\) )。\(1\) 和 \(2\) ,一奇一偶,那我们可以大胆假设 \(s\) 与 \(t\) 之间距离为奇数时输出 \(1\),为偶数时输出 \(2\)。
但是 \(1e6\) 次询问,如果每一次都求一遍路径长的话肯定会 \(TLE\) 。那我们应该怎么办呢?既然正解想不出,那就先看部分分吧。
第一个部分分可能是给每一次询问都暴力求距离的( 我不太确定 )。对思考没什么帮助,跳过。
第二个部分分规定 \(G\) 图是一棵树。树有什么性质呢?那我们来随便画一棵树并对它的节点进行编号找找规律吧。( 标号顺序为 \(Felling ~ first\) )
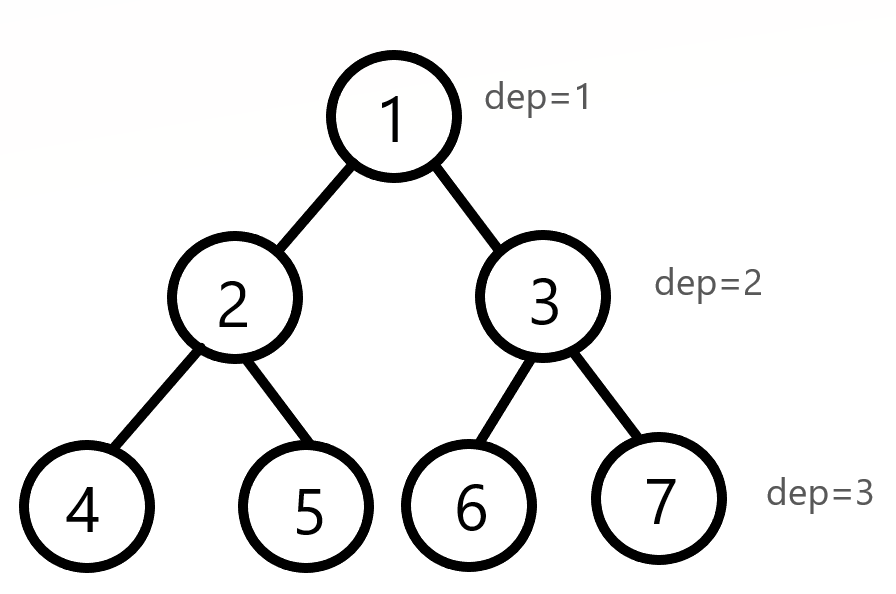
由图,我们不难发现,深度相差为偶数的两个点之间的距离一定为偶数,深度相差为奇数的两个点之间的距离一定为奇数。那我们不妨简化一下这棵树的深度
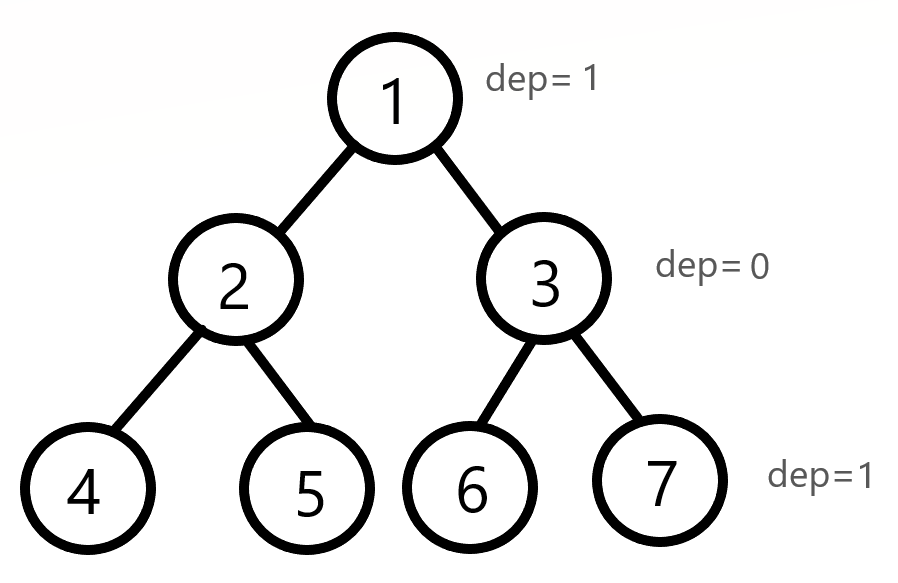
这样的话 \(dep\) 相同的两个点距离为偶数, \(dep\) 不同的两个点之间的距离为奇数。
那这个部分分我们就做完了,但是我们可以由此尝试推一下图的性质。我们不妨把一个图看做是一棵树加上几条非树边。
由于我们已经根据深度的不同将点分为两类:\(dep=1\) 和 \(dep=0\) ,所以这里的非树边我们也可以分为两种:连接同层点,连接异层点。
通过手模我们可以发现如果这个非树边连接的是同层点,那么任意两点之间的距离一定为奇数;若非树边连接的是异层点,则该非树边不会对答案造成干扰。
代码:
$code$
#include<iostream>
using namespace std;
const int N=1e6+5;
int T,n,m,u,v,q,s,t,tot,cnt,head[N],dfn[N],dep[N];bool vis[N];
struct wutong{int to,nxt;}jade[N<<1];
inline void add(int a,int b){
jade[++cnt].to=b;jade[cnt].nxt=head[a];head[a]=cnt;
jade[++cnt].to=a;jade[cnt].nxt=head[b];head[b]=cnt;
}
inline void dfs(int x){
for(int i=head[x];i;i=jade[i].nxt){
int y=jade[i].to;
if(dfn[y]) continue;
dfn[y]=dfn[x];dep[y]=(dep[x]+1)%2;
dfs(y);
}
}
int main(){
// freopen("teleport.in","r",stdin);
// freopen("teleport.out","w",stdout);
ios::sync_with_stdio(false);
cin>>T;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>u>>v;
add(u,v);
}
for(int i=1;i<=n;i++) if(!dfn[i]) dfn[i]=i,dep[i]=1,dfs(i);
for(int x=1;x<=n;x++){
for(int i=head[x];i;i=jade[i].nxt){
int y=jade[i].to;
if(dep[x]==dep[y]) vis[dfn[x]]=1;
}
}
cin>>q;
while(q--){
cin>>s>>t;
if(s==t) cout<<0<<'\n';
else if(dfn[s]!=dfn[t]) cout<<-1<<'\n';
else if(dep[s]!=dep[t]||vis[dfn[s]]) cout<<1<<'\n';
else cout<<2<<'\n';
}
return 0;
}
T3:先辈(anc)
首先感谢大佬的二次讲解%%%
我们先观察一下题目中多次出现的数字—— \(114514\)
我们不难发现这里面只有三个数字,所以我们的第一反应是枚举这三个数字分别代表什么字母,此时的时间复杂度为 \(O(n*26^3)\) 。
这样肯定会 \(TLE\) 。那我们就要想如何能够少枚举点东西呢?
众所周知,柿子要捡软的捏(bushi),那么我们舍弃的肯定就是作用最小的那个咯。
那很显然 \(5\) 只出现了一次,那么它的影响应该就是最小的了。我们只需要保证它跟 \(1\) 和 \(4\) 所代表的字母不同就好了。
这样我们的时间复杂度就降到了 \(O(n*26^2)\)
愉快的交上去,发现还是 \(TLE\) 了。
为什么呢?因为 驱魔 取模太慢了,所以我们再转变一下取模的方式就好啦~~
代码:
$code$
#include<iostream>
#include<cstring>
#define add(x,y) x+=y,x=x>=mod?x-mod:x
using namespace std;
const int N=5e5+5,mod=114514;
int a[N],ans,n,maxn=-1,minn=1e9;
char ch[N];
inline void dfs(int s1,int s2){
int len1=0,len2=0,len3=0,len4=0,len5=0,len6=0;
for(int i=1;i<=n;i++){
if(a[i]==s1) add(len5,len4),add(len2,len1),add(len1,1);//一定要倒着加呀!
else if(a[i]==s2) add(len6,len5),add(len3,len2);
else add(len4,len3);
}add(ans,len6);
}
signed main(){
// freopen("anc.in","r",stdin);
// freopen("anc.out","w",stdout);
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>(ch+1);
n=strlen(ch+1);
for(int i=1;i<=n;i++) a[i]=ch[i]-'0'+1,maxn=max(maxn,a[i]),minn=min(minn,a[i]);
for(int i=minn;i<=maxn;i++){
for(int j=minn;j<=maxn;j++){
if(i==j) continue;
dfs(i,j);
}
}cout<<ans%mod;
return 0;
}
T4:矩阵(matrix)
思路:
我们把这里的矩阵看做是一张图的邻接矩阵。
那么题目所要求的就是一个无环且不存在长度为 \(k+1\) 的链的图最多有多少条边。
那我们就把所有点均分为 \(k\) 份,同份之间的点不连边,不同份之间的点从前向后连边。最后记得处理一下余数就好了
代码:
$code$
#include<iostream>
#define int long long
using namespace std;
int n,k,ans;
signed main(){
// freopen("matrix.in","r",stdin);
// freopen("matrix.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n>>k;
if(n<=k){
cout<<(n*(n-1)>>1);
return 0;
}
while(n){
int w=n/k;
int t=n/(w+1);
int delta=k-t;
ans+=w*(delta*(n-w+n-w*delta)>>1);
n-=w*delta;
k=t;
}cout<<ans;
return 0;
}
后言:
后面的是今天赶的,有点点遗忘但是时间不允许我去回顾题面,所以写的很仓促,等明天有时间了再细补。



