李超线段树
前言:
这里图比较多,奈何本人手残,图画得很烂,还改了好几版,只能是尽量看吧......
概念
李超线段树是一个可以维护平面直角坐标系内各个直线的关系的数据结构。
它支持动态插入线段,查询给定\(x\)对应的\(y\)的最值。
例如:【模板】李超线段树
下面根据例题进行实现过程的具体讲解。
既然这个名字带有线段树,那么它的实现过程肯定与线段树相关或相似,也分为建树,修改,查询三部分。
\(Part\,\ 1:\) 建树
建树的方式与普通线段树大差不差,其他的小点根据题意去维护就好啦,就不再赘述啦~~
\(Part\,\ 2:\) 修改
这里我们要用到分讨的思想,要分为好多好多种情况。
\((1)\) 该线段与区间不交
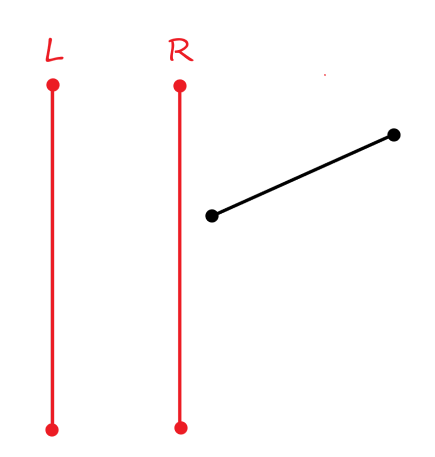
那就没有必要进行修改了,因为很显然,此时这条线段对答案无影响。
\((2)\) 该线段完全包含该区间
① 新加的边完全大于原来的边
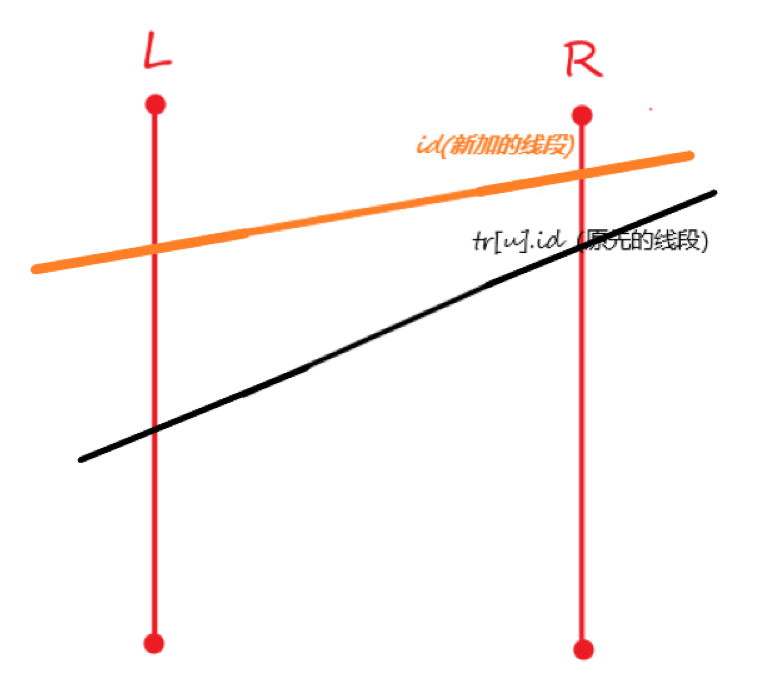
此时把原本记录的边替换为新加的这条边。
if(cmp(id,tr[u].id,l)&&cmp(id,tr[u].id,r)){
tr[u].id=id;
return ;
//cmp是一个比较函数,等一下会解释,先莫急
}
②新建的边完全小于原来的边
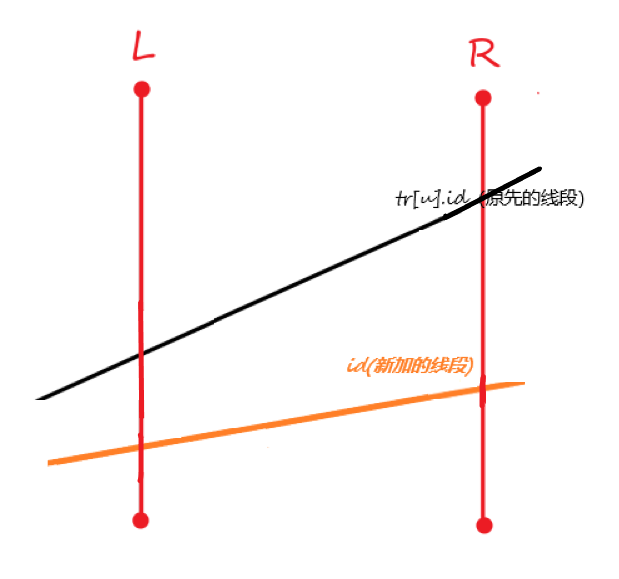
此时新加的边对答案无影响,所以不用修改。
if(cmp(tr[u].id,id,l)&&cmp(tr[u].id,id,r)) return ;
③在\(mid\)处,新加入的边比较大
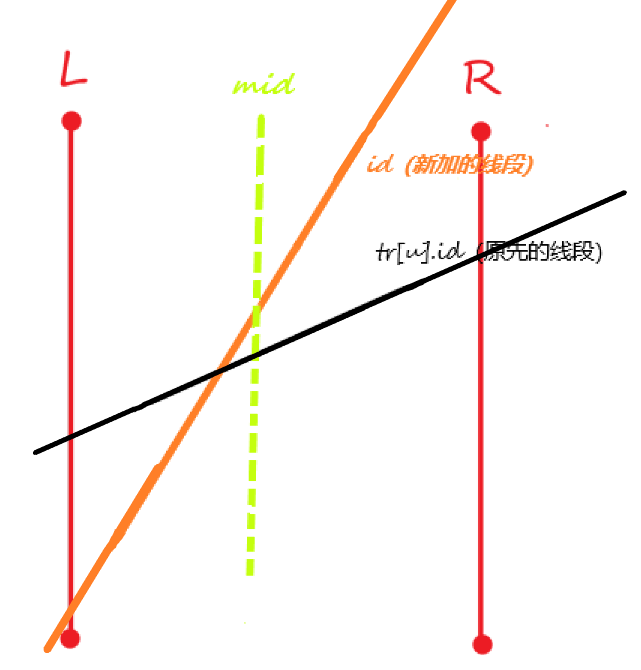
此时,在当前区间,新边作为更优答案的概率更大,所以交换\(id\)和\(tr[u].id\)的值。否则不用交换。此时无论是否交换,图都变成如下。(以后说的边都是交换完以后的边)。
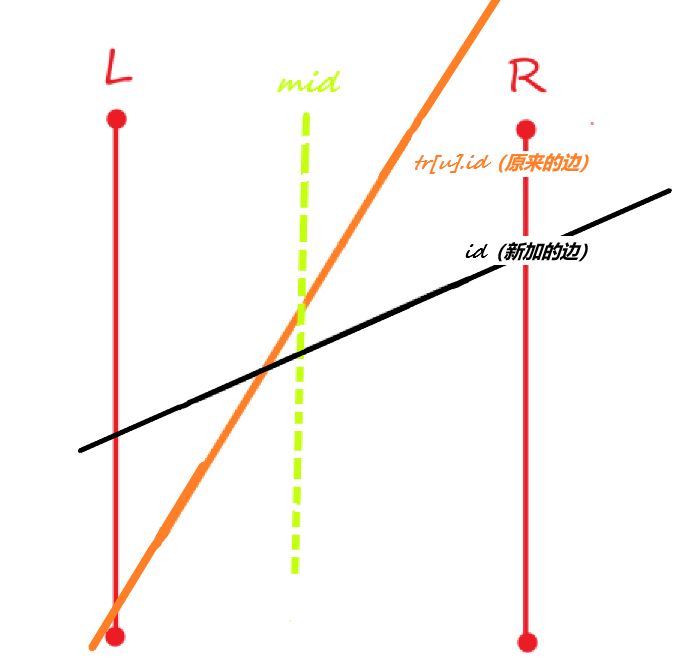
if(cmp(id,tr[u].id,mid)) swap(id,tr[u].id);
④如果新建边的\(l\)的值要大的话,证明在\(l\)~\(mid\)这个区间内两条线段相交,因此继续递归前半个区间(如上图)
if(cmp(id,tr[u].id,l)) insert(tr[u].l,l,mid,L,R,id);
⑤如果新建边的\(r\)值要大的话,证明两条线在区间\(mid\)~\(r\)内相交,因此继续递推后半个区间。(如下图)
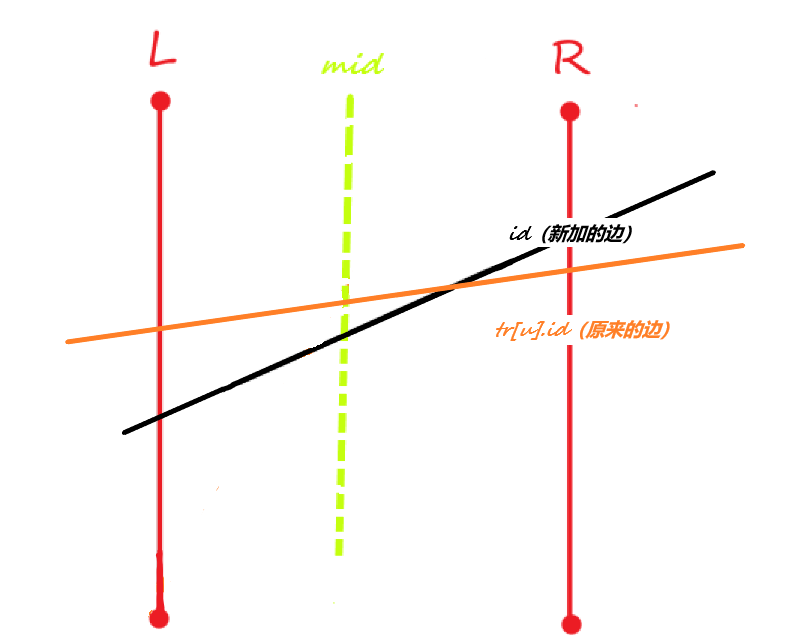
if(cmp(id,tr[u].id,r)) insert(tr[u].r,mid+1,r,L,R,id);
\((3)\)这条线段的一部分在区间内
这是我们需要折半递归区间,直到区间的某一部分完全被该线段覆盖。
insert(tr[u].l,l,mid,L,R,id);
insert(tr[u].r,mid+1,r,L,R,id);
\(Part\,\ 3:\) 查询
\((1)\) 该区间不包含所查询的那个值
此时没有必要继续递推下去,结束就好了。
if(!u||r<x||x<l) return ;
\((2)\)该区间包含所要查询的值
如果现在遍历到的那个节点的值大于目前的答案,那就更新答案。
if(cmp(tr[u].id,ans,x)) ans=tr[u].id;
\((3)\)区间不可再分
此时没有其他情况了,可以结束递推了。
if(l==r) return;
\((4)\)区间可以继续分割
为了保证答案的正确性,我们需要遍历每一个可能对答案造成影响的线段,因此我们需要继续向下搜索。
query(tr[u].l,l,mid,x);
query(tr[u].r,mid+1,r,x);
\(Part\,\ 4:\) 代码时间~~
线段
#include<iostream>
#define int long long
using namespace std;
const double eps=1e-1;
const int mod1=39989,mod2=1e9,N=2e5+5;
int n,x0,x1,y0,y1,ans,lastans,Lcnt,cnt,root,k;bool op;
struct Line{double k,b;}line[N];//维护线段相关信息
struct Tree{int l,r,id;}tr[N<<2];//维护线段树
inline double caly(int i,int x){return line[i].k*x+line[i].b;}//计算纵坐标
inline bool cmp(int i,int j,int x){
if(caly(i,x)-caly(j,x)>eps) return true;
if(caly(j,x)-caly(i,x)>eps) return false;
return i<j;
}//设计小数,使用精度比较大小
inline void insert(int &u,int l,int r,int L,int R,int id){
if(r<L||R<l) return ;
if(!u) u=++cnt;//动态开点线段树
if(L<=l&&r<=R){
if(cmp(id,tr[u].id,l)&&cmp(id,tr[u].id,r)){
tr[u].id=id;
return ;
}
if(cmp(tr[u].id,id,l)&&cmp(tr[u].id,id,r)) return ;
int mid=(l+r)>>1;
if(cmp(id,tr[u].id,mid)) swap(id,tr[u].id);
if(cmp(id,tr[u].id,l)) insert(tr[u].l,l,mid,L,R,id);
if(cmp(id,tr[u].id,r)) insert(tr[u].r,mid+1,r,L,R,id);
}else{
int mid=(l+r)>>1;
insert(tr[u].l,l,mid,L,R,id);
insert(tr[u].r,mid+1,r,L,R,id);
}
}//插入
inline void query(int u,int l,int r,int x){
if(!u||r<x||x<l) return ;
if(cmp(tr[u].id,ans,x)) ans=tr[u].id;
if(l==r) return;
int mid=(l+r)>>1;
query(tr[u].l,l,mid,x);query(tr[u].r,mid+1,r,x);
}//查询
signed main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>op;
if(op==1){
cin>>x0>>y0>>x1>>y1;//输入
x0=(x0+lastans-1)%mod1+1;
x1=(x1+lastans-1)%mod1+1;
y0=(y0+lastans-1)%mod2+1;
y1=(y1+lastans-1)%mod2+1;//强制在线
if(x1<x0) swap(x1,x0),swap(y1,y0);
Lcnt++;
if(x1!=x0){
line[Lcnt].k=1.0*(y1-y0)/(x1-x0);
line[Lcnt].b=1.0*y0-line[Lcnt].k*x0;
}else{
line[Lcnt].k=0;
line[Lcnt].b=max(y0,y1);
}//计算斜率和纵截距
insert(root,1,mod1,x0,x1,Lcnt);//插入 因为x值肯定不大于mod1,所以区间右端点就设为mod1.
}else if(op==0){
cin>>k;//输入
k=(k+lastans-1)%mod1+1;//强制在线
ans=0;//多组数据初始化
query(1,1,mod1,k);//查询 同插入
cout<<ans<<'\n';
lastans=ans;
}
}
return 0;
}
直线
$code$
#include<iostream>
using namespace std;
const int N=1e5+5;
const double eps=1e-8;
int n,root,t,cnt,num;
string ch;
double s,p,res,ans;
struct flower{
double k,b;
}line[N];
struct css{
int l,r,x;
}tr[N<<2];
inline double calc(int id,int x){
return line[id].k*(x-1)+line[id].b;
}
inline bool cmp(int i,int j,int x){
if(calc(i,x)-calc(j,x)>eps) return false;
if(calc(j,x)-calc(i,x)>eps) return true;
return i<j;
}
inline void insert(int &rt,int l,int r,int id){
if(r<l) return ;
if(!rt) rt=++num;
if(!tr[rt].x){
tr[rt].x=id;
return ;
}
int mid=(l+r)>>1;
if(cmp(tr[rt].x,id,mid)) swap(id,tr[rt].x);
if(cmp(tr[rt].x,id,l)) insert(tr[rt].l,l,mid,id);
if(cmp(tr[rt].x,id,r)) insert(tr[rt].r,mid+1,r,id);
}
inline double query(int rt,int l,int r,int x){
if(!rt||l>x||r<x) return 0;
double ans=calc(tr[rt].x,x);
if(l==r) return ans;
int mid=(l+r)>>1;
if(x<=mid) ans=max(ans,query(tr[rt].l,l,mid,x));
else ans=max(ans,query(tr[rt].r,mid+1,r,x));
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin>>n;
while(n--){
cin>>ch;
if(ch=="Query"){
cin>>t;
int ans=max(0.00,query(root,1,50000,t)/100);
cout<<ans<<'\n';
}else{
cin>>s>>p;
line[++cnt].k=1.0*p;
line[cnt].b=1.0*s;
insert(root,1,50000,cnt);
}
}
return 0;
}
复杂度分析
先摆结论,这个东西的时间复杂度是\(O(log^2~n)\)的。
不严谨的证明:首先,众所周知,线段树建树是\(O(log~n)\)的。然后,区间二分递推也是\(O(log~n)\)的。所以,综上所述,复杂度是\(O(log^2~n)\)
补充:
插入部分有另一种写法,那种写法可以更好地分析时间复杂度,但是原理是一样的。不过我比较懒,不想再打了,所以给你们偷了个链过来
具体代码为:

嘿嘿,粘代码是不可能粘的,粘张图吧~~
update:2025年10月26日
先存代码:
$code$
#include<iostream>
#define int long long
using namespace std;
const int N=1e5+5,inf=1e18;
int n,u,v,a[N],b[N],cnt,tot,head[N],rt[N];
struct flower{
int k,b;
}line[N];
struct css{
int l,r,x;
}tr[N<<3];
struct miss{
int to,nxt;
}e[N<<1];
inline void add(int x,int y){
e[++tot].to=y;e[tot].nxt=head[x];head[x]=tot;
e[++tot].to=x;e[tot].nxt=head[y];head[y]=tot;
}
inline int calc(int id,int x){
return line[id].k*x+line[id].b;
}
inline bool cmp(int i,int j,int x){
if(calc(i,x)>calc(j,x)) return true;
else return false;
}
inline void insert(int &rt,int l,int r,int id){
if(!rt) rt=++cnt;
if(!tr[rt].x){
tr[rt].x=id;
return ;
}
int mid=(l+r)>>1;
if(calc(id,mid)<calc(tr[rt].x,mid)) swap(id,tr[rt].x);
if(calc(id,l)<calc(tr[rt].x,l)) insert(tr[rt].l,l,mid,id);
if(calc(id,r)<calc(tr[rt].x,r)) insert(tr[rt].r,mid+1,r,id);
}
inline int query(int rt,int l,int r,int x){
if(!rt) return inf;
int ans=calc(tr[rt].x,x);
if(l==r) return ans;
int mid=(l+r)>>1;
if(x<=mid) ans=min(ans,query(tr[rt].l,l,mid,x));
else ans=min(ans,query(tr[rt].r,mid+1,r,x));
return ans;
}
inline int merge(int x,int y,int l,int r){
if(!x||!y) return x+y;
if(l==r){
if(calc(tr[x].x,l)>calc(tr[y].x,l)) return y;
return x;
}
int mid=(l+r)>>1;
tr[x].l=merge(tr[x].l,tr[y].l,l,mid);
tr[x].r=merge(tr[x].r,tr[y].r,mid+1,r);
insert(x,l,r,tr[y].x);
return x;
}
inline void dfs(int x,int fa){
int f=0;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa) continue;
f++;
dfs(y,x);
rt[x]=merge(rt[x],rt[y],-N,N);
}
line[x].k=b[x];
if(f) line[x].b=query(rt[x],-N,N,a[x]);
else line[x].b=0;
insert(rt[x],-N,N,x);
}
signed main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<n;i++){
cin>>u>>v;
add(u,v);
}
dfs(1,0);
for(int i=1;i<=n;i++) cout<<line[i].b<<' ';
return 0;
}


