李超线段树
你说什么?我一上午就敲了个板子?
李超线段树
定义
李超线段树是一种用于维护多条一次函数的线段树。你可以使用它在\(O(logn)\)的复杂度内插入一条新的直线,或是查询所有直线\(y=k_ix+b_i\)中,当\(x=x_0\)时,\(y\) 的最值。
例题
洛谷 P4097 【模板】李超线段树 / [HEOI2013] Segment

理论
插入
线段树上每个节点维护\(x=\frac {l+r} {2}\)处的最高点的 \(y\)和线段编号。
对于区间\(l~r\),插入一条新线段。
- 该线段与区间\(l~r\)没有交集
因此对区间内维护的最优线段没有影响;
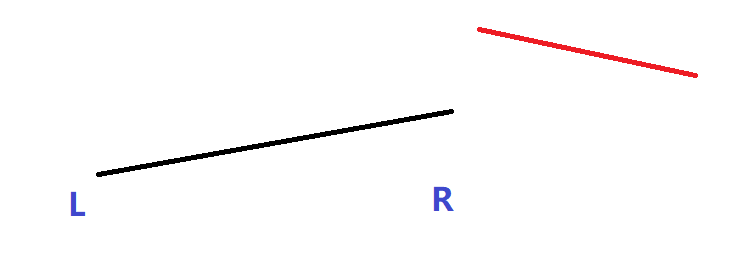
- 该线段与区间\(l~r\)有交集,但区间不是该线段定义域的子集
此时考虑递归到该区间的左右子区间作进一步细化处理;
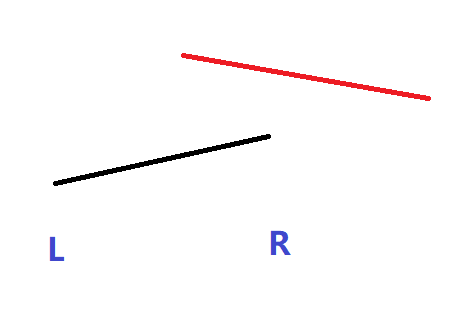
- 区间\(l~r\)是该线段定义域的子集
此时分三种情况分类讨论原区间\(l~r\)中的最优线段和新加线段的位置关系:
(红色为新线段,黑色为老线段即原最优线段)
- 新线段在老线段的上方时:直接更新即可。
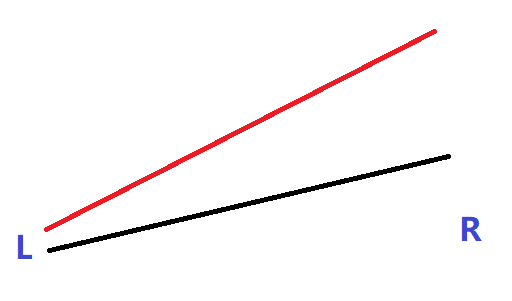
-
新线段在老线段的下方时:丢弃。
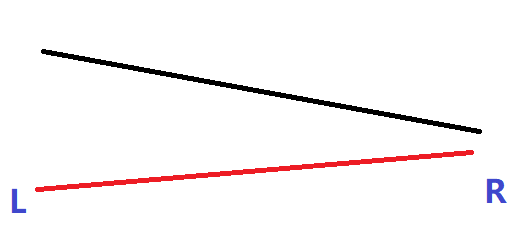
-
新线段和老线段交叉时:
设点\(x\)是线段树上的一个节点,\(mid\)是\(x\)所代表的区间的中点。
原来,使\(y\)取到最大值的直线编号是\(t[x]\)(即黑色线段),现在新增的直线编号是\(now\) (即红色线段)。
我们比较在区间中点 \(mid\) 两条线段对应的纵坐标谁大,将大的那条作为新的最优线段(即老线段)。
但由于这两条线段相互之间都不能被对方完全覆盖,所以考虑将没成为最优线段的那条线段往该区间的左右子区间下放,作递归处理(只需要往有比最优线段更优的一端递归即可)。
如图:
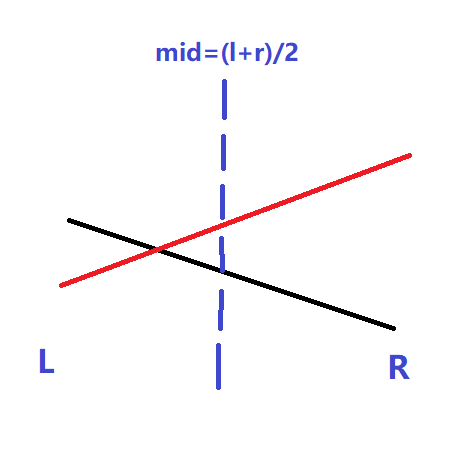
红色的线段为新线段,黑色的线段为老线段(即原最优线段),比较两个线段上当\(x=mid\)时\(y\)的大小,发现新线段的\(y\)更大,交换新线段和老线段。
如图
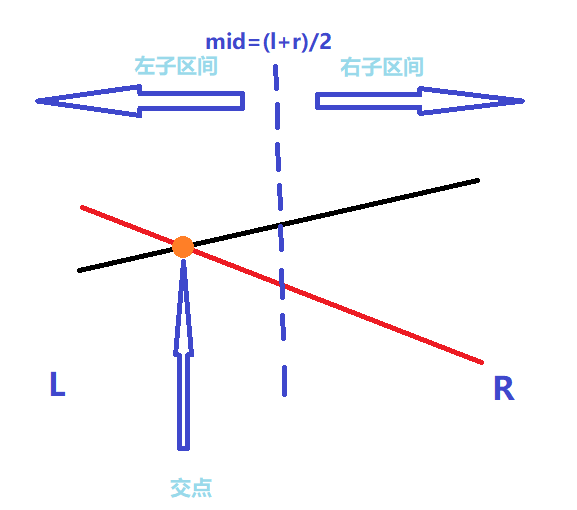
判断可知新线段(即红色线段)的左区间端点比老线段要大,递归更新左区间。判断出右区间新线段不优,即不能对答案做出贡献,丢弃。
每一次都只会修改左右区间中的\(1\)个,时间复杂度为\(O(log^2n)\)。我们把这种对 区间修改、单点查询 起效的方法称作“标记永久化”。
查询
单点查询。
需要注意的是由于 标记永久化 的存在,路径上遇到的任意一个答案都可能是最终的答案,而叶子节点处可能根本没有记录答案。
所以需要将路径上遇到的所有答案取最值作为最终结果。
如上图中右区间的任意一个点的答案都在 \(x\) 节点处被记录,而没有继续往下传递。所以需要在 \(x\) 处求出答案并和其它可能答案取 \(max\) 。
实现
代码
#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1)
const double eps=1e-10;//调精度
const int mod=39989;
const int _mod=1e9;
int n,op,k,xx,xy,yx,yy;
int ans,lastans,lcnt;
struct jade
{
double k,b;//直线参数
}line[100010];//线段
struct seek
{
int l,r,id;//区间左右端点//编号
}t[400010];
//李超线段树
void build(int ro,int l,int r)
{
t[ro].l=l;
t[ro].r=r;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
double gety(int i,int x)//计算纵坐标
{
return line[i].k*x+line[i].b;
}
bool cmp(int i,int j,int x)//比较编号为 i 和 j 的线段在 X 处的纵坐标
{
if(gety(i,x)-gety(j,x)>eps)
{
return 1;
}
if(gety(j,x)-gety(i,x)>eps)
{
return 0;
}
return i<j;
}
void insert(int ro,int l,int r,int id)//插入线段,编号为 id
{
if(t[ro].r<l||t[ro].l>r)//线段与该区间不交
{
return ;
}
if(l<=t[ro].l&&r>=t[ro].r)//线段完全覆盖该区间,区间是该线段定义域的子集
{
if(cmp(id,t[ro].id,t[ro].l)&&cmp(id,t[ro].id,t[ro].r))//该线段比当前区间最优线段完全更优
{
t[ro].id=id;
return ;
}
if(cmp(id,t[ro].id,t[ro].l)==0&&cmp(id,t[ro].id,t[ro].r)==0)//该线段比当前区间最优线段完全更劣
{
return ;
}
//两线段有交点,都不能完全覆盖彼此
int mid=(t[ro].l+t[ro].r)>>1;
if(cmp(id,t[ro].id,mid))
{
swap(id,t[ro].id);
}
//处理左右子区间
if(cmp(id,t[ro].id,t[ro].l))
{
insert(ls,l,r,id);
}
if(cmp(id,t[ro].id,t[ro].r))
{
insert(rs,l,r,id);
}
}
else//线段覆盖部分该区间
{
//处理左右子区间
insert(ls,l,r,id);
insert(rs,l,r,id);
}
}
void query(int ro,int x)
{
if(t[ro].r<x||t[ro].l>x)
{
return ;
}
if(cmp(t[ro].id,ans,x))//比较路径上的最优线段,记录编号
{
ans=t[ro].id;
}
if(t[ro].l==t[ro].r)
{
return ;
}
//在树上往下查询最优线段
query(ls,x);
query(rs,x);
}
int main()
{
cin>>n;
build(1,1,mod);
for(int i=1;i<=n;i++)
{
cin>>op;
if(op==0)
{
cin>>k;
k=(k+lastans-1)%mod+1;
ans=0;
query(1,k);
cout<<ans<<endl;
lastans=ans;
}
else
{
cin>>xx>>xy>>yx>>yy;
xx=(xx+lastans-1)%mod+1;
yx=(yx+lastans-1)%mod+1;
xy=(xy+lastans-1)%_mod+1;
yy=(yy+lastans-1)%_mod+1;
if(yx<xx)
{
swap(xx,yx);
swap(xy,yy);
}
lcnt++;
if(yx!=xx)
{
line[lcnt].k=1.0*(yy-xy)/(yx-xx);
line[lcnt].b=1.0*xy-line[lcnt].k*xx;
}
else//特殊处理竖直线段
{
line[lcnt].k=0;
line[lcnt].b=max(xy,yy);
}
insert(1,xx,yx,lcnt);
}
}
return 0;
}
来自机房大蛇们的另一种做法
即把原insert函数拆为insert和add,分开处理线段与区间的交集情况。
add处理线段与区间的关系,若完全覆盖则调用insert加入线段,此时因区间全覆盖所以只传参\(id\)和\(ro\)。
反之则add函数向左右儿子递归。
add函数的时间复杂度为\(O(\log n)\),insert函数的时间复杂度也为\(O(\log n)\),合并起来为\(O(\log^2n)\),时间复杂度相同。
#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1)
const double eps=1e-10;//调精度
const int mod=39989;
const int _mod=1e9;
int n,op,k,xx,xy,yx,yy;
int ans,lastans,lcnt;
struct jade
{
double k,b;//直线参数
}line[100010];//线段
struct seek
{
int l,r,id;//区间左右端点//编号
}t[400010];
//李超线段树
void build(int ro,int l,int r)
{
t[ro].l=l;
t[ro].r=r;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
double gety(int i,int x)//计算纵坐标
{
return line[i].k*x+line[i].b;
}
bool cmp(int i,int j,int x)//比较编号为 i 和 j 的线段在 X 处的纵坐标
{
if(gety(i,x)-gety(j,x)>eps)
{
return 1;
}
if(gety(j,x)-gety(i,x)>eps)
{
return 0;
}
return i<j;
}
void insert(int ro,int id)//插入直线,编号为 id
{
if(cmp(id,t[ro].id,t[ro].l)&&cmp(id,t[ro].id,t[ro].r))//该直线比当前区间最优线段完全更优
{
t[ro].id=id;
return ;
}
if(cmp(id,t[ro].id,t[ro].l)==0&&cmp(id,t[ro].id,t[ro].r)==0)//该直线比当前区间最优线段完全更劣
{
return ;
}
//两线段有交点,都不能完全覆盖彼此
int mid=(t[ro].l+t[ro].r)>>1;
if(cmp(id,t[ro].id,mid))
{
swap(id,t[ro].id);
}
//处理左右子区间
if(cmp(id,t[ro].id,t[ro].l))
{
insert(ls,id);
}
if(cmp(id,t[ro].id,t[ro].r))
{
insert(rs,id);
}
return ;
}
void add(int ro,int l,int r,int id)
{
if(t[ro].r<l||t[ro].l>r)//线段与该区间不交
{
return ;
}
if(l<=t[ro].l&&r>=t[ro].r)//线段完全覆盖该区间,区间是该线段定义域的子集
{
insert(ro,id);
return ;
}
//线段覆盖部分该区间
//处理左右子区间
add(ls,l,r,id);
add(rs,l,r,id);
}
void query(int ro,int x)
{
if(t[ro].r<x||t[ro].l>x)
{
return ;
}
if(cmp(t[ro].id,ans,x))//比较路径上的最优线段,记录编号
{
ans=t[ro].id;
}
if(t[ro].l==t[ro].r)
{
return ;
}
//在树上往下查询最优线段
query(ls,x);
query(rs,x);
}
int main()
{
cin>>n;
build(1,1,mod);
for(int i=1;i<=n;i++)
{
cin>>op;
if(op==0)
{
cin>>k;
k=(k+lastans-1)%mod+1;
ans=0;
query(1,k);
cout<<ans<<endl;
lastans=ans;
}
else
{
cin>>xx>>xy>>yx>>yy;
xx=(xx+lastans-1)%mod+1;
yx=(yx+lastans-1)%mod+1;
xy=(xy+lastans-1)%_mod+1;
yy=(yy+lastans-1)%_mod+1;
if(yx<xx)
{
swap(xx,yx);
swap(xy,yy);
}
lcnt++;
if(yx!=xx)
{
line[lcnt].k=1.0*(yy-xy)/(yx-xx);
line[lcnt].b=1.0*xy-line[lcnt].k*xx;
}
else//特殊处理竖直线段
{
line[lcnt].k=0;
line[lcnt].b=max(xy,yy);
}
add(1,xx,yx,lcnt);
}
}
return 0;
}
我们发现,如果线段树维护的是直线,则使用\(O(\log n)\)做法即可完成修改操作,因为不用判断区间,多用于DP优化方面。
例题2.0(NOIP2025模拟1 C. 舰队的远征)
更新于2025/11/4
今天是第一场noip模拟赛,炸炸炸,改改改。
神秘的T3可以用李超线段树写,但我又懒得新开一篇博客,所以就归类到李超线段树的例题里惹(QAQ是因为根本没空写,现在还在施工的有"CSP-S 2025 游记","2-SAT学习笔记"…………)
题面link
赛时
花4min写了一个弗洛伊德,创了40pts,太傻比了所以就不展开讲讲了
正解
dij预处理+李超线段树
hiahiahiahiahiahiahiahiahiahihahaihaihai(这题卡SPFA!!😦 )
发现如果没有隐藏能源,这题是平凡的(我直接一个单源最短路),但考虑其消耗燃料的表达式,设临时通道的起点为\(x\),终点是\(y\),其舰队从\(s\)出发,抵达\(t\),则有:
tips:
\(dis_s[x]\)表示从\(s\)出发到\(x\)点的最短路。
\(dis_t[y]\)表示从\(t\)出发到\(y\)点的最短路。
这两个东西可以用两遍\(dij\)跑出来,但区别是一个在正向建边的图跑,另一个是在反向建边的图跑。
啊这东西即\(x\)又\(y\)的不太好优化,考虑将它拆开
考虑枚举\(x\),发现\(dis_s[y]+y^2-2\times xy\)形如一次函数\(y=kx+b\)的形式,然后套用李超线段树求解给定\(x\)关于\(y\)的最小贡献(即使\(dis_t[y]+y^2-2\times xy\)最小),然后加上枚举\(x\)得到的\(dis_s[x]+x^2\)值,最后在\(n\)个答案中取最小值即可。
代码实现
#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1)
struct jade
{
long long l,r,id;
}tr[800010];
long long n,m,s,t;
long long h[200010],to[400010],nxt[400010],v[400010],tot;
long long dis[200010];
bool vis[200010];
long long _h[200010],_to[400010],_nxt[400010],_v[400010],_tot;
long long _dis[200010];
bool _vis[200010];
long long k[200010],b[200010];
long long cnt;
void add(long long x,long long y,long long val)
{
tot++;
to[tot]=y;
nxt[tot]=h[x];
v[tot]=val;
h[x]=tot;
}
void _add(long long x,long long y,long long val)
{
_tot++;
_to[_tot]=y;
_nxt[_tot]=_h[x];
_v[_tot]=val;
_h[x]=_tot;
}
void dij()
{
memset(dis,0x3f,sizeof(dis));
priority_queue<pair<long long,long long>,vector<pair<long long,long long>>,greater<>>q;
q.push(make_pair(0,s));
dis[s]=0;
while(!q.empty())
{
long long x=q.top().second;
q.pop();
if(vis[x])
{
continue;
}
vis[x]=1;
for(long long i=h[x];i;i=nxt[i])
{
long long y=to[i];
if(dis[y]>dis[x]+v[i])
{
dis[y]=dis[x]+v[i];
q.push(make_pair(dis[y],y));
}
}
}
}
void _dij()
{
memset(_dis,0x3f,sizeof(_dis));
priority_queue<pair<long long,long long>,vector<pair<long long,long long>>,greater<>>q;
q.push(make_pair(0,t));
_dis[t]=0;
while(!q.empty())
{
long long x=q.top().second;
q.pop();
if(_vis[x])
{
continue;
}
_vis[x]=1;
for(long long i=_h[x];i;i=_nxt[i])
{
long long y=_to[i];
if(_dis[y]>_dis[x]+_v[i])
{
_dis[y]=_dis[x]+_v[i];
q.push(make_pair(_dis[y],y));
}
}
}
}
void build(long long ro,long long l,long long r)
{
tr[ro].l=l;
tr[ro].r=r;
if(l==r)
{
return ;
}
long long mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
long long js(long long id,long long x)
{
return k[id]*x+b[id];
}
bool cmp(long long i,long long j,long long x)
{
if(js(i,x)>js(j,x))
{
return 0;
}
return 1;
}
void insert(long long ro,long long id)
{
if(cmp(id,tr[ro].id,tr[ro].l)&&cmp(id,tr[ro].id,tr[ro].r))
{
tr[ro].id=id;
return ;
}
if(cmp(id,tr[ro].id,tr[ro].l)==0&&cmp(id,tr[ro].id,tr[ro].r)==0)
{
return ;
}
long long mid=(tr[ro].l+tr[ro].r)>>1;
if(cmp(id,tr[ro].id,mid))
{
swap(id,tr[ro].id);
}
if(cmp(id,tr[ro].id,tr[ro].l))
{
insert(ls,id);
}
if(cmp(id,tr[ro].id,tr[ro].r))
{
insert(rs,id);
}
}
void query(long long ro,long long x)
{
if(tr[ro].r<x||tr[ro].l>x)
{
return ;
}
if(cmp(tr[ro].id,cnt,x))
{
cnt=tr[ro].id;
}
if(tr[ro].l==tr[ro].r)
{
return ;
}
query(ls,x);
query(rs,x);
}
int main()
{
freopen("far.in","r",stdin);
freopen("far.out","w",stdout);
cin>>n>>m>>s>>t;
for(long long i=1;i<=m;i++)
{
long long x,y,val;
cin>>x>>y>>val;
add(x,y,val);
_add(y,x,val);
}
dij();
_dij();
k[0]=0;
b[0]=1e18;
for(long long i=1;i<=n;i++)
{
k[i]=-2*i;
b[i]=_dis[i]+i*i;
}
build(1,1,n);
for(long long i=1;i<=n;i++)
{
insert(1,i);
}
long long ans=1e18;
for(long long i=1;i<=n;i++)
{
cnt=0;
query(1,i);
long long res=dis[i]+i*i+b[cnt]+i*k[cnt];
ans=min(ans,res);
}
cout<<ans;
return 0;
}
不开longlong见祖宗
李超线段树合并优化DP
李超/线段树合并/优化DP
更新于2025/10/25
模莫默模拟赛的T4正解是李超/线段树合并/优化DP,其实也属于动态开点部分。
发现我的李超线段树连板子都忘得差不多了,这题还是Pursuing_OIer学长讲过的原题(对不起)
于是回炉重造一下。
定义
你问我啥是李超线段树合并优化DP,其实就是李超/线段树合并/优化DP,额就是用动态开点的李超线段树做李超线段树合并维护斜率来优化DP。
你可以把它看成李超线段树+动态开点+线段树合并+DP
还是不知道?那就看一下例题:
例题
(模莫默模拟赛原题哈哈哈因为数据太水放过了许多\(n^2\))
洛谷 CF932F Escape Through Leaf

考虑\(DP\),设\(dp[i]\)为从x出发到叶子节点的最小代价(即答案),发现一个十分显然(但不会维护的)动态转移方程:
直接转移是\(O(n^2)\)的,肯定过不了(如果数据不那么水的话)
将 \(dp_y,b_y\)分别看作 \(b,k\)发现其很像一次函数的形式,此题又要求该方程的最值。(应该算斜率优化DP?优化斜率DP)
考虑使用李超线段树维护。
但发现每一次转移都需要一颗李超线段树,时间复杂度是\(O(n\log n^2)\)的,太坏惹!
然后就是(李超)线段树合并了。
时间复杂度\(O(n\log n)\)
细节请看代码实现:
代码
#include<bits/stdc++.h>
using namespace std;
struct jade
{
long long k,b;//斜率,截率
int id;//标号
}line[400010];//存线段
int n,a[100010],b[100010];//输入
long long dp[100010];//dp状态
int h[100010],to[200010],nxt[200010],tot;//链式前向星
int rt[2000010],ls[2000010],rs[2000010],js;//动态开点李超线段树
void add(int x,int y)//存图
{
tot++;
to[tot]=y;
nxt[tot]=h[x];
h[x]=tot;
}
long long get_y(jade i,int x)//找纵坐标
{
return i.k*x+i.b;
}
long long lsi_x(jade x,jade y)//找交点
{
return (x.b-y.b)/(y.k-x.k);
}
void insert(int &ro,int l,int r,jade ln)//动态开点插入一条线段
{
if(!ro)
{
js++;
ro=js;
}
int mid=(l+r)>>1;
if(get_y(line[ro],mid)>get_y(ln,mid)||!line[ro].id)//更换新老线段
{
swap(line[ro],ln);
}
if(l==r||line[ro].k==ln.k||!ln.id)
{
return ;
}
long long pos=lsi_x(line[ro],ln);//找交点
if(pos<l||pos>r)
{
return ;
}
if(ln.k>line[ro].k)
{
insert(ls[ro],l,mid,ln);
}
else
{
insert(rs[ro],mid+1,r,ln);
}
}
int merge(int x,int y,int l,int r)//李超线段树合并
{
if(!x||!y)
{
return x+y;
}
insert(x,l,r,line[y]);
int mid=(l+r)>>1;
ls[x]=merge(ls[x],ls[y],l,mid);//左儿子
rs[x]=merge(rs[x],rs[y],mid+1,r);//右儿子
return x;
}
jade find(int ro,int l,int r,int x)//区间查找
{
if(l==r)
{
return line[ro];
}
int mid=(l+r)>>1;
jade res;
if(mid>=x)
{
res=find(ls[ro],l,mid,x);
}
else
{
res=find(rs[ro],mid+1,r,x);
}
if(!res.id||get_y(line[ro],x)<get_y(res,x))
{
return line[ro];
}
return res;
}
void dfs(int x,int fa)//树形DP
{
for(int i=h[x];i;i=nxt[i])
{
int y=to[i];
if(y==fa)
{
continue;
}
dfs(y,x);
rt[x]=merge(rt[x],rt[y],-100000,100000);//值域
}
int minn=find(rt[x],-100000,100000,a[x]).id;
dp[x]=1ll*a[x]*b[minn]+dp[minn];//dp方程
insert(rt[x],-100000,100000,{b[x],dp[x],x});
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
cin>>b[i];
}
for(int i=1;i<n;i++)
{
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
dfs(1,0);
for(int i=1;i<=n;i++)
{
cout<<dp[i]<<" ";
}
return 0;
}
动态开点李超线段树
正在施工中...
广义李超线段树
正在施工中...
未完待续...
本文来自博客园,作者:BIxuan—玉寻,转载请注明原文链接:https://www.cnblogs.com/zhangyuxun100219/p/19056743



 浙公网安备 33010602011771号
浙公网安备 33010602011771号