CSP-S模拟12
前言:
虽然考的一如既往地不咋地 (其实是超级烂) ,但是同志我还是来写题解了。嘿嘿!
T1:114514(trans)
题面(懒得手打了 直接粘图吧):

样例输入1:
6
1 2 4 5 3 6
样例输出1:
72
样例输入2:
7
2 9 3 10 8 4 1
样例输出2:
12
样例输入3:
20
7 8 1 2 3 12 13 9 10 11 18 19 20 14 16 17 4 5 15 6
样例输出3:
149299200
数据范围:
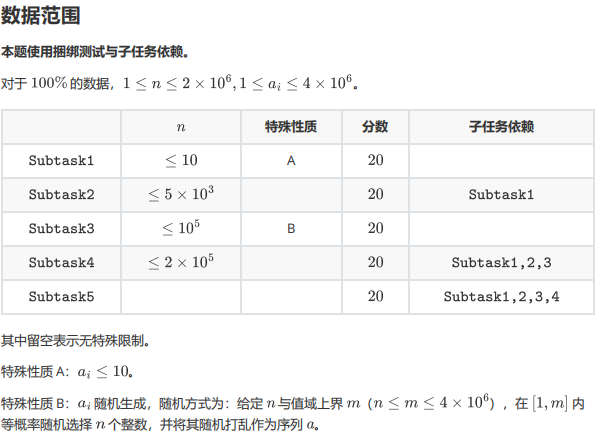
思路:
手模一遍样例,你就会发现这个问题有点类似于区间覆盖(语出:肝硬化),一提到区间覆盖最简单的操作应该就是饼茶鸡(并查集)了吧(个人观点 好叭,其实已经被学妹否认了)其实我也不是很理解为什么要用并查集 (不然也不至于考这么点烂分) ,肝硬化说是因为:要从当前点向下搜索,寻找连续的被覆盖的路径。下面附上一张巨丑的图供大家参考理解(千万不要误人子弟呀!)
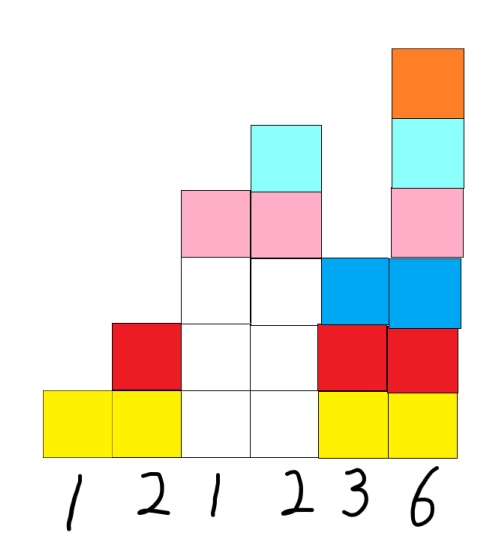
因此,答案为\(ans=1×2×1×2×3×6=72.\)
但是此时算法的时间复杂度为\(O(n^2)\),显然是不可接受的,因此考虑优化。这里的优化是使用路径压缩。这里就需要请出我们的并查集啦!
具体优化过程为:每次将\(a_i\)合并到\(a_i-1\)上面,这样复杂度就降为\(O(n)\)的啦!于是,我们就这样愉快的AC啦~~
代码:
点击查看代码
#include<iostream>
#define int long long//记得开long long(三年oi一场空,_________。)
using namespace std;
const int N=2e6+5,M=4e6+5,mod=1e9+7;
int n,sum=1,ans,a[N],fa[N<<1];bool t[N<<1];
inline int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}//路径压缩
inline void merge(int x,int y){
x=find(x);y=find(y);
if(x==y) return ;
fa[y]=x;
}//合并
//以上两个都是并查集的板子 就不过多赘述了
signed main(){
// freopen("trans.in","r",stdin);
// freopen("trans.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=M-5;i++) fa[i]=i;//并查集的模板:初始化
for(int i=1;i<=n;i++){
t[a[i]]=1;//标记存在
if(t[a[i]-1]){//向下搜索连续的路径
ans=find(a[i]-1);//找到符合条件的最低点
sum=sum%mod*(a[i]-ans+1)%mod;//求答案
merge(a[i]-1,a[i]);//向下合并方便下次使用
}if(t[a[i]+1]) merge(a[i],a[i]+1);//同上 不过这个是向上合并
//需要向上合并是为了把前面存在但是没有连接上的点连接上
//eg. ...14 16 15...
//需要在遍历到15的时候向上把16也连接上(其实应该不是什么难点,但是奈何本人较菜,所以补充一下~)
}
cout<<sum%mod<<'\n';//最后再输出答案就好啦
return 0;//完结撒花
}
T2:沉默乐团(orchestra)
题面:

样例输入1:
4
1 1
2 2
3 3
10 10
样例输出1:
1
样例输入2:
1
1 2000
样例输出2:
2000
样例输入3:
4
1 2
1 2
1 2
1 2
样例输出3:
2
样例输入4:
5
1 3
2 4
1 4
1 2
3 3
样例输出4:
18
样例输入5:
6
1 5
1 5
1 5
1 5
1 5
1 5
样例输出5:
5120
数据范围:
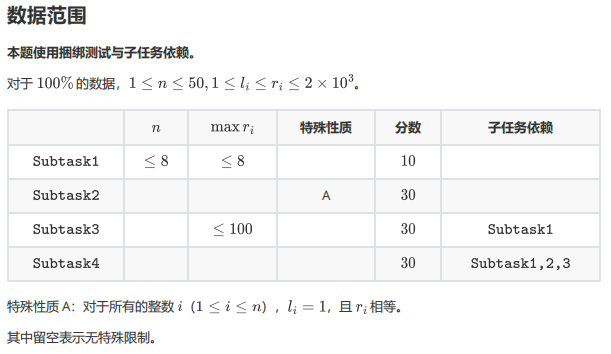
思路:
首先,看到题目会想到使用\(DP\)。但是具体原因我是说不出来的,可能是因为有统计方案数,所以往\(DP\)方面想了想,好像也满足使用DP的几个条件,那这道题基本上就八九不离十就得使用\(DP\)了。由题意可设状态为\(f[i][j][k]\)表示\(1\) ~ \(i\)(以下简称为前半部分)对应的序列的和与\(j\) ~ \(n\)(以下简称为后半部分)对应的序列的和的差为\(k\).
想到这里,那转移方程也就不远了。让我们分讨一下:
-
\(k>0\),此时前半部分大于后半部分,那我们就让\(j\)向前转移,此时的方程由\(f[i][j-1][k+x](x为当前位对应的值)\)转移而来。
-
\(k<0\),此时前半部分小于后半部分,那我们就让\(i\)向后转移,此时的方程由\(f[i+1][j][k-x](x为当前位对应的值)\)转移而来。
因为当\(i=1,j=n\)时,序列的前后都没有数字了,所以此时差值为\(0\)。因此,我们最后输出的答案为\(f[1][n][0]\)。
你以为这就完了吗?还不可以哦。此时的时间复杂度为\(O(n^2m^2)\)这当然是不可以接受的啦。所以,我们同样需要考虑优化呢。
这里的优化比较简单,就是使用前缀和和差分来优化时间,这样我们的时间复杂度就变为了优秀的\(O(n^2m)\)。这样我们就可以通过此题啦~~
对了,还有一个小性质差点忘说。就是:若一段前缀和一段后缀相等且有交, 那么一定存在一段前缀和后缀相等且无交。(其实不难理解,自己手模一遍就好啦。)
算鸟算鸟,我还是给你们摆个 (图) 丑图吧:
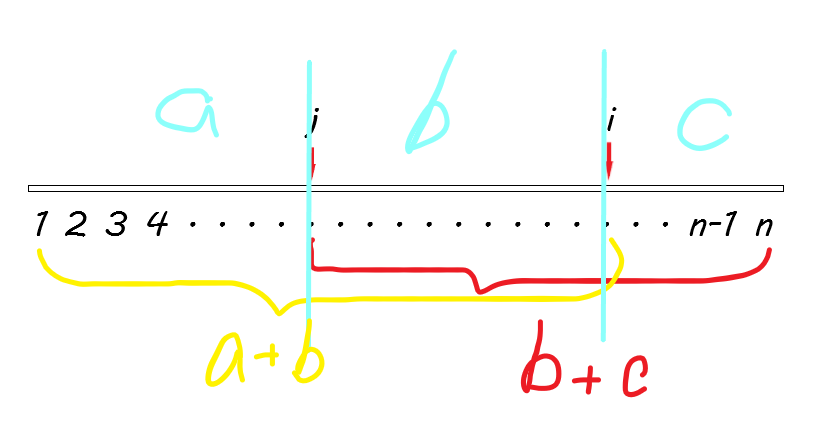
反证法:假设前半部分等于后半部分,即\(a+b=b+c\)。所以,由小学数学可得 \(a=c\)。所以我们就不用考虑\(i\)和\(j\)重叠的问题啦~
大体思路已经结束了,再让我们来关注一下些细节叭。众所周知,数组的下标不能为负数。那怎么办呢?由于我们知道k的范围为\(-2000\) ~ \(2000\),所以我们不妨给k整体加上一个偏移量2000(好像有点废话...)然后应该就没啥了,其他的具体操作见代码叭~~
代码:
点击查看代码
#include<iostream>
using namespace std;
const int N=55,M=4005,level=2000,mod=1e9+7;
int n,l[N],r[N],f[N][N][M],s[N][N][M];//数量 区间范围 dp求值 前缀和
int main(){
// freopen("orchestra.in","r",stdin);
// freopen("orchestra.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) cin>>l[i]>>r[i];
for(int i=1;i<=n;i++){
for(int k=0;k<=4000;k++)
if(k!=level||n==1)
f[i][i][k]=s[i][i][k]=r[i]-l[i]+1-(abs(k-level)>=l[i]&&abs(k-level)<=r[i]);
//初始化 这里比较难理解(个人认为)思路放最下面了
for(int k=1;k<=4000;k++) s[i][i][k]=(s[i][i][k]+s[i][i][k-1])%mod;//前缀和
}
for(int len=2;len<=n;len++){//这一步自己把len,i,j都输出一遍就知道为啥了【嗯嗯】
for(int i=1,j=len;j<=n;i++,j++){//遍历i,j
//cout<<"len="<<len<<" i="<<i<<" j="<<j<<endl;
for(int k=0;k<=level;k++){//第一种情况
if(k!=level||(i==1&&j==n)) //记得考虑 i=1且j=n的特殊情况
f[i][j][k]=(s[i+1][j][k+r[i]]-s[i+1][j][k+l[i]-1]+mod)%mod;
}
for(int k=level+1;k<=4000;k++) //第二种情况
f[i][j][k]=(s[i][j-1][k-l[j]]-s[i][j-1][k-r[j]-1]+mod)%mod;
for(int k=1;k<=4000;k++) s[i][j][k]=(s[i][j][k-1]+f[i][j][k])%mod;//再次更新前缀和
}
}
cout<<f[1][n][level]<<'\n';//输出答案
return 0;//完结撒花~~
}
-
初始化:
这句话的意思是如果前半部分和后半部分的差值在这个点对应的\(l\) ~ \(r\) 的区间范围内的话,需要减去当前值为差值的那种情况,因为这种情况下该序列不合法。(可能比较抽象。。。看不懂先别慌,继续往下看!)
举个栗子: 反证法!
我们不妨令当前值为差值。
此时\(i\)和\(j\)在同一个位置上,如下图:
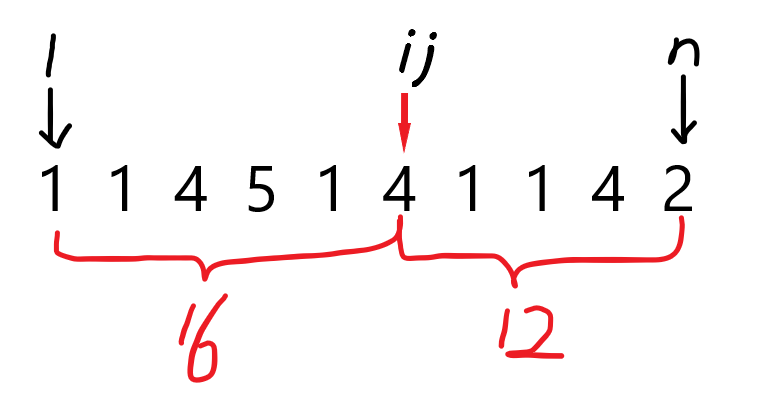
此时的序列看起来没有什么问题。但是如果仔细观察的话,你会发现这个序列并不合法,请看VCR下图:
当\(i\)和\(j\)在如下位置的时候,很显然,序列不合法。
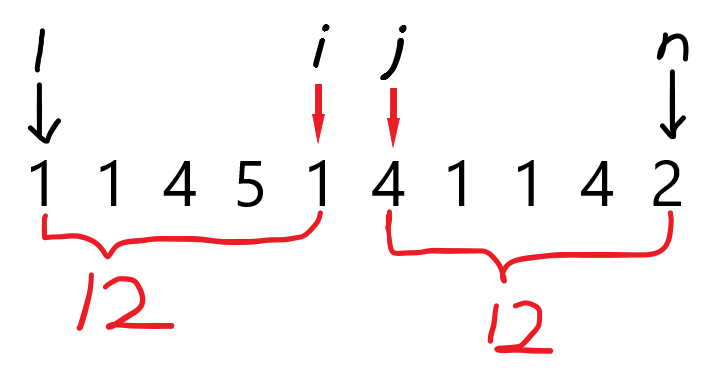
-
\(len\)的作用:
我们需要逐步扩展k的值,即从相邻每一个字之差,相邻每两个数字之差......以此类推,直到\(i=1,j=n\)时结束扩展,求出答案。


