CSP-S模拟12——类人群星闪耀时
写在前面
这次模拟赛总体感觉思维难度较大,思路及代码实现方面对于肝硬化来说都还是太超前了。 \(T1\) 赛时花了 \(10minutes\) 想出疑似正确的思路,开场 \(30minutes\) 打完 \(O(n^2)\) 的暴力,期望 \(40\) ~ \(60pts\) ,怕逆天数据把暴力卡掉于是绞尽脑汁想了一个或许可行的优化,结果写的递归炸了 \(1.5hours\) ,最终写出一个疑似绝对跑不满的 \(O(n^2)\) 但实际 \(O(n)\) (我也不知道,题解说这是线性那就是了)的做法,结果和暴力代码跑了遍样例发现均比暴力慢一点点,身心俱疲,遂交上去,期望 \(60pts+\) ;\(T2\) 逆天求和公式瞪了半年才发现是错的,然后看到数据范围果断暴力先拿十分再说,想冲特殊性质 \(A\) 但是不会,暴搜也炸了递归调了 \(30minutes\) (肝硬化怎么总是写炸递归?),最终期望 \(10pts\) ; \(T3\) 过于神秘,花了 \(15minutes\) 理解了题意,又花了 \(30minutes\) 写了个统计逆序对个数,发现自己根本不会搞,于是多次尝试后未果,寻病终,直接跳到 \(T4\),期望 \(0pts\)(根本就没交好吧!!!); \(T4\) 看到题果断暴搜,递归又改了 \(30minutes\) 发现假了,样例死活过不去,仅剩 \(15minutes\) 于是交上,期望 \(0pts\) ,画了会儿画,发了会儿呆,视奸了会儿鱼鱼,遗憾离场,期望 \(60+10+0+0=70pts\) ,实际 \(100+10+0+0=110pts\),此时肝硬化才意识到它的 \(T1\) 打的就是正解。
为什么叫做“类人群星闪耀时”呢?为了标题党博眼球因为某机房大牢(此处省略姓名)爆十了( \(T1~RE\) , \(T2\) 打的十分暴力);某 \(HZOI~T1\) 挂分大王(此处省略姓名2.0)因为 \(T1~4hours\) 没调出来爆零了遗憾离场………
开始题解!
T1 114514
好臭的名字,奠定了整场恶臭的基础。
题目背景(有史慎看)

题目描述



样例1
输入
6
1 2 4 6 3 6
输出
72
样例2
输入
7
2 9 3 10 8 4 1
输出
12
样例3
输入
20
7 8 1 2 3 12 13 9 10 11 18 19 20 14 16 17 4 5 15 6
输出
149299200
数据范围
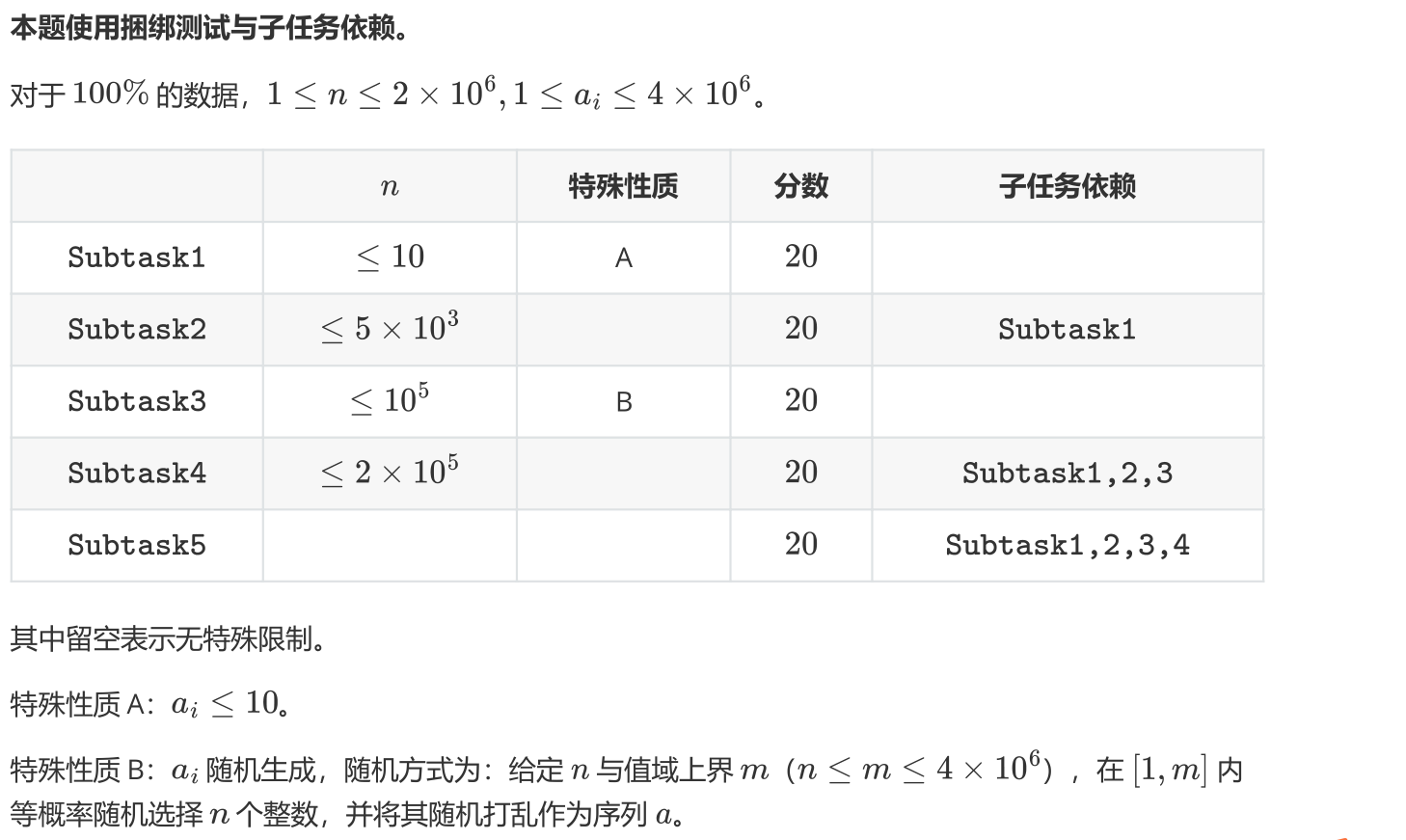
Solve
首先我们观察一下前两个样例,可以发现每个位置可以取的值是这样的【!!!鬼图警告!!!】↓
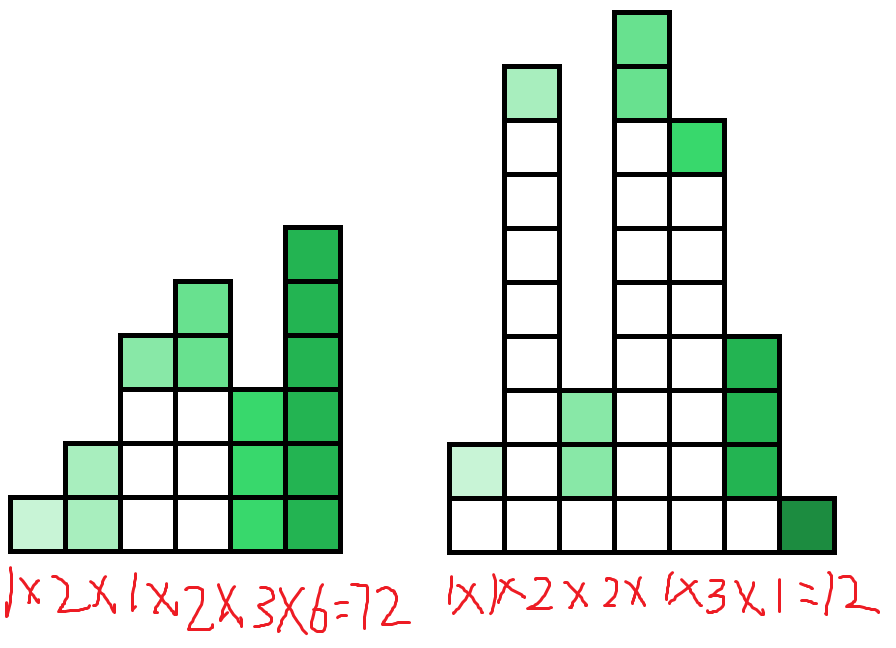
我们可以发现,首先每一列最大的数一定能选,然后每一列从最大的数减一开始,如果在它前面这个数被选过,那么它也可以被选;如果没有,那么它和比它小的所有数在当前列都不能选(自己根据题意理解一下,很好懂的【确信!】)
-那么就可以写出 \(n^2\) 的做法啦!
-可是会 \(TLE\) 啊。
-别急,往下看。
考虑到刚刚发现的性质,我们可以开一个 \(to\) 数组表示从当前位置的数可以向下找到的最远的数,往下查找的时候顺便做一个路径压缩(其实用了并查集的·思想,可能算是赛时肝硬化yy出的一个并查集罢…其实正解就是并查集/单调栈),这样可以大大节省时间,达到 \(O(n)\) 的优秀复杂度!
Code
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int _ = 2e6 + 10;
const int mod = 1e9 + 7;
int n, to[4000010], a[_];
long long ans = 1;
inline int find(int x, int bfr){
if(! to[x]){
return bfr;
}
if(to[x] != x){
return to[x] = find(to[x] - 1, to[x]);
}
if(to[x] == x){
return to[x] = find(x - 1, x);
}
}
int main(){
freopen("trans.in", "r", stdin);
freopen("trans.out", "w", stdout);
scanf("%d", & n);
for(int i = 1; i <= n; i ++){
scanf("%d", & a[i]);
to[a[i]] = a[i];
if(! to[a[i] - 1]){
continue;
}
int r = find(a[i], 1);
ans = (ans * (a[i] - r + 1)) % mod;
}
printf("%lld", ans);
return 0;
}
T2 沉默乐团
出题入是月计人【雾】
题目背景

题目描述



样例1
输入
4
1 1
2 2
3 3
10 10
输出
1
样例2
输入
1
1 2000
输出
2000
样例3
输入
4
1 2
1 2
1 2
1 2
输出
2
样例4
输入
5
1 3
2 4
1 4
1 2
3 3
输出
18
样例5
输入
6
1 5
1 5
1 5
1 5
1 5
1 5
输出
5120
样例解释

数据范围
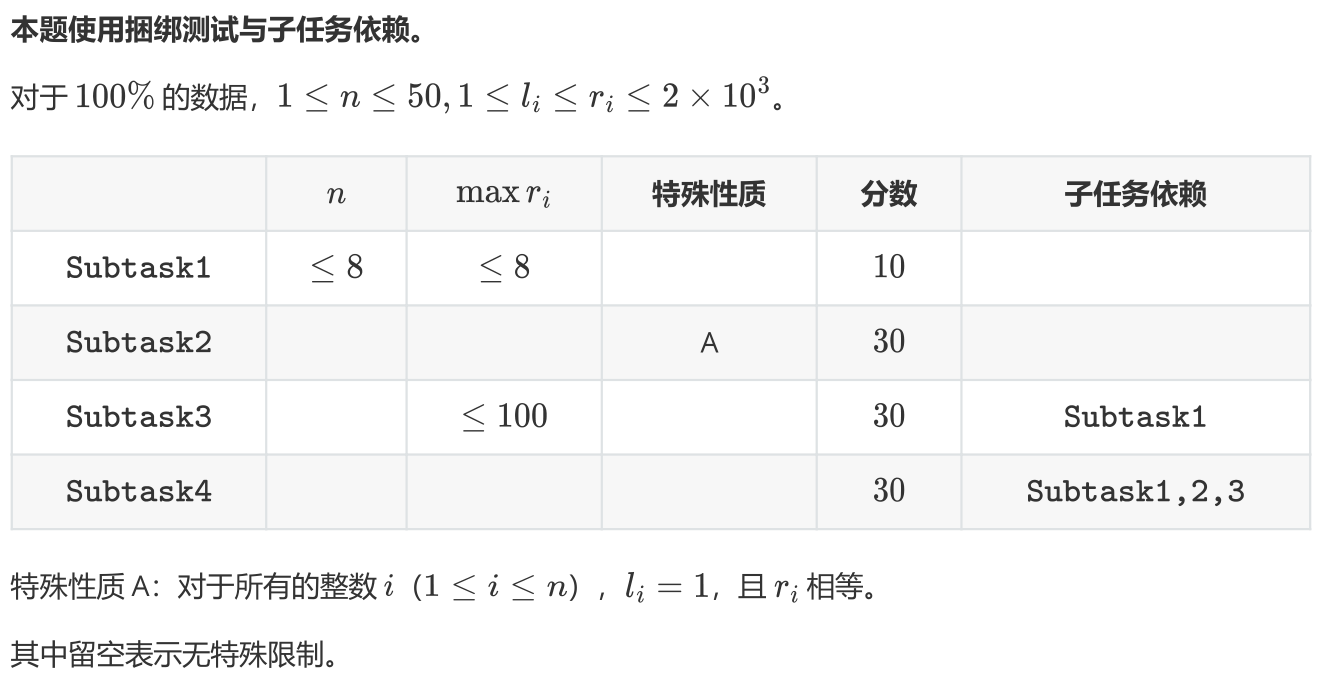
Solve
十分的暴力想必大家都会我就不多赘述了喵。
-首先可以发现,题目中那个诡异的求和公式等价于不存在一对真前缀和真后缀的和相等。
-所以你想表达什么?
-所以我们可以发现一个性质:如果这对真前缀和真后缀相交,那么一定存在一对不相交的真前缀和真后缀的和也相等。
-为什么?
-假设和相等的前后缀分别为区间 \([1,i]\) 和 \([j,n](i >= j)\) ,那么 \([1,j-1]\) 和 \([i+1,n]\) 两边都减去了 \([j,i]\) 的和,它俩也相等且不相交。
-原来如此!
于是我们可以用双指针 \(O(n)\) 来判断:如果前缀和大于后缀和,我们就将右指针左移,否则将左指针右移。如果存在一个时刻前后缀和相等,那么序列就不合法了,直接扔掉。
因为要求方案数,于是可以轻(绞)而(尽)易(脑)举(汁)地想到DP:设 \(f_{i,j,k}\) 表示当前左指针在 \(i\) ,右指针在 \(j\) ,且当前前缀和减后缀和的差为 \(k\) 的方案数,最后答案即为 \(f_{1,n,0}\) 。
考虑如何转移:还是像双指针的过程一样,如果 k>0 ,代表前缀和大于后缀和,我们需要将右指针左移,也就是 \(f_{i,j,k}←f_{i,j−1,k−x}\) ,其中 \(x∈[lj,rj]\) 。当 \(k<=0\) 也是同理,但是挪的是左指针。直接转移是 \(O(n^2 V^2)\) 的,好像听到了TLE的回响,使用前缀和可以优化到 \(O(n^2V)\)。
在实现上,可以使用 \(map\) 或者加上一个偏移量防止下标出现负数。
-如何预处理?
-看这里 \(sum\) 是前缀和, \(dp\) 是 \(f\), \(l\) , \(r\) 为题目输入的数, \(k\) 意义与上文意义相同。↓
for(int i = 1; i <= n; i ++){
for(int k = 0; k <= 4000; k ++){
if(k != mx || n == 1){
dp[i][i][k] = sum[i][i][k] = r[i] - l[i] + 1 - (abs(k - mx) <= r[i] && abs(k - mx) >= l[i]);
}
}
-别的我懂了,但是为什么要减去 abs(k - mx) <= r[i] && abs(k - mx) >= l[i] 呢?
-让我们看一个已经选出来的序列↓
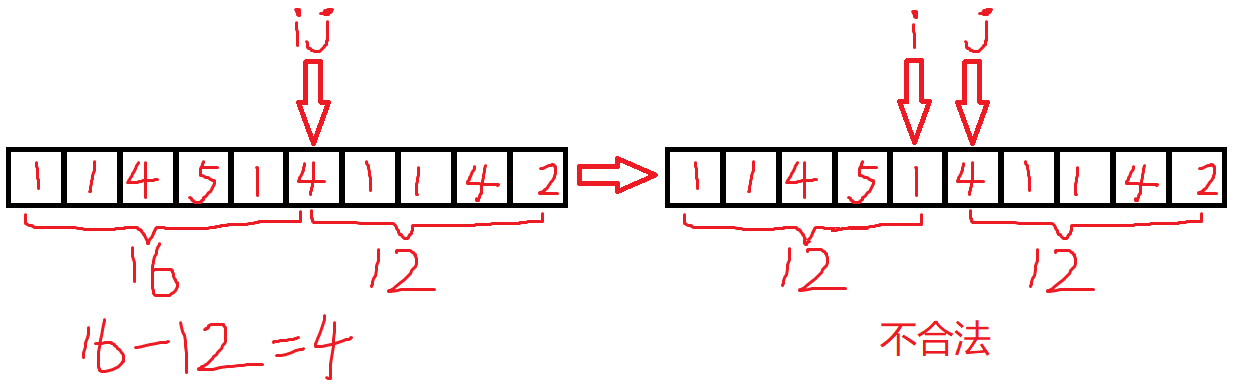
(因为左边的图前缀和大于后缀和,所以左指针需要向左移。)
-我懂了,这样的序列是不合法的,我们不能将它作为答案的一环!!!
-然后剩下的部分就很好懂啦,直接看代码!
Code
#include <bits/stdc++.h>
using namespace std;
const int _ = 55;
const int __ = 4e3 + 10;
const int mx = 2000;
const int mod = 1e9 + 7;
int n, dp[_][_][4010], sum[_][_][4010], l[_], r[_];//数组不要开小!!!
int main(){
freopen("orchestra.in", "r", stdin);
freopen("orchestra.out", "w", stdout);
scanf("%d", & n);
for(int i = 1; i <= n; i ++){
scanf("%d%d", & l[i], & r[i]);
}
for(int i = 1; i <= n; i ++){
for(int k = 0; k <= 4000; k ++){
if(k != mx || n == 1){
dp[i][i][k] = sum[i][i][k] = r[i] - l[i] + 1 - (abs(k - mx) <= r[i] && abs(k - mx) >= l[i]);
}
}
for(int k = 1; k <= 4000; k ++){
sum[i][i][k] += sum[i][i][k - 1];
sum[i][i][k] %= mod;
}
}
for(int o = 2; o <= n; o ++){
for(int i = 1, j = o; j <= n; i ++, j ++){
for(int k = 0; k <= mx; k ++){
if(k != mx || (i == 1 && j == n)){
dp[i][j][k] = (sum[i + 1][j][k + r[i]] - sum [i + 1][j][k + l[i] - 1] + mod) % mod;
}
}
for(int k = mx + 1; k <= 4000; k ++){
dp[i][j][k] = (sum[i][j - 1][k - l[j]] - sum[i][j - 1][k - r[j] - 1] + mod) % mod;
}
sum[i][j][0] = dp[i][j][0];
for (int k = 1; k <= 4000; k ++){
sum[i][j][k] = (sum[i][j][k - 1] + dp[i][j][k]) % mod;
}
}
}
printf("%d", dp[1][n][mx]);
return 0;
}
T3 深黯[军团]
?我不会,赛时暴力都没想出来怎么打(详情见写在前面),先鸽了喵。
T4 终末螺旋
?我也不会,赛时暴力都打假了(详情见卸载钱main),咕咕咕。
END.
拜拜了您内~
本文来自博客园,作者:养鸡大户肝硬化,转载请注明原文链接:https://www.cnblogs.com/rain20100708/p/19042682

 近千百年间rank最高的一集。
近千百年间rank最高的一集。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号