题解：[ICPC 2022 Seoul R] Empty Quadrilaterals

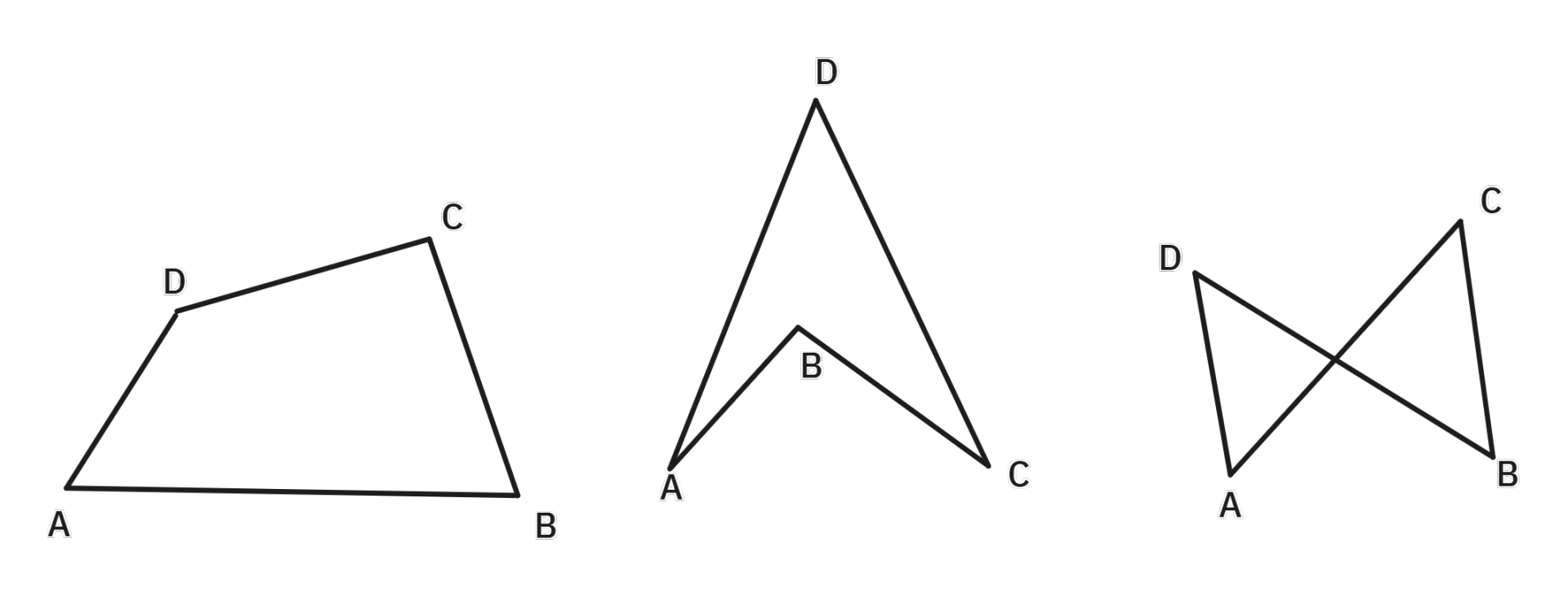
由四个点四条边构成的图形有以上三种，其中前两种符合题目要求，称为凸四边形和凹四边形。

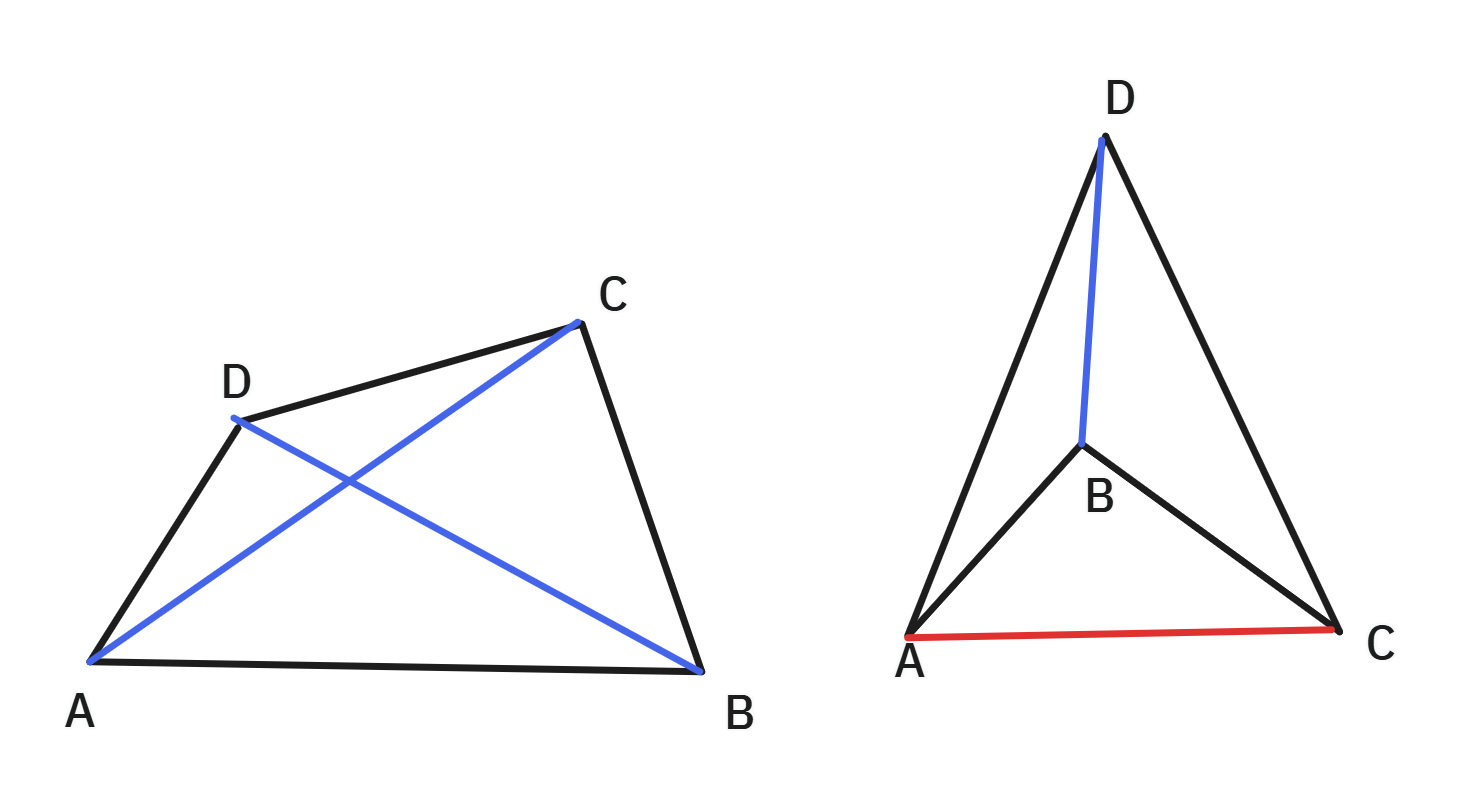
为了计数不包含其它点的四边形，考虑枚举一些东西。从时间复杂度上考虑，枚举一个点信息太少，枚举三个点已经 \(\mathcal O(n^3)\) 的复杂度，很难再做别的部分了，所以枚举两个点比较合适。一个想法是枚举一条边，但会发现对于凹四边形限制很奇怪。除了边外，四边形中顶点连线就只有对角线了。设枚举的对角线为 \(XY\)，一个四边形恰好有两条对角线，可以分为两两种情况：

1. 内部对角线：上图中的蓝色对角线，凸四边形的全部两条对角线和凹四边形的其中一条对角线是这种。这种对角线会将四边形分成 \(XY\) 两侧各一个三角形，计数只需要分别统计 \(XY\) 左侧有 \(c_L\) 个 \(P\) 满足 \(\triangle PXY\) 中没有其他点，左侧有 \(c_R\) 个 \(Q\) 满足 \(\triangle QXY\) 中没有其他点，\(c_L\times c_R\) 即为 \(XY\) 以作为内部对角线的四边形数量。
2. 外部对角线：上图中的红色对角线，凹四边形的另一条对角线是这种。此时，另外两个顶点一定是在 \(XY\) 的同一侧，要统计的就是有多少对点 \(P,Q\)，满足 \(\triangle PXY\) 内部的其他点恰好是 \(\triangle QXY\) 内部的其他点加上点 \(Q\)（显然一个 \(P\) 至多对应一个 \(Q\)）。

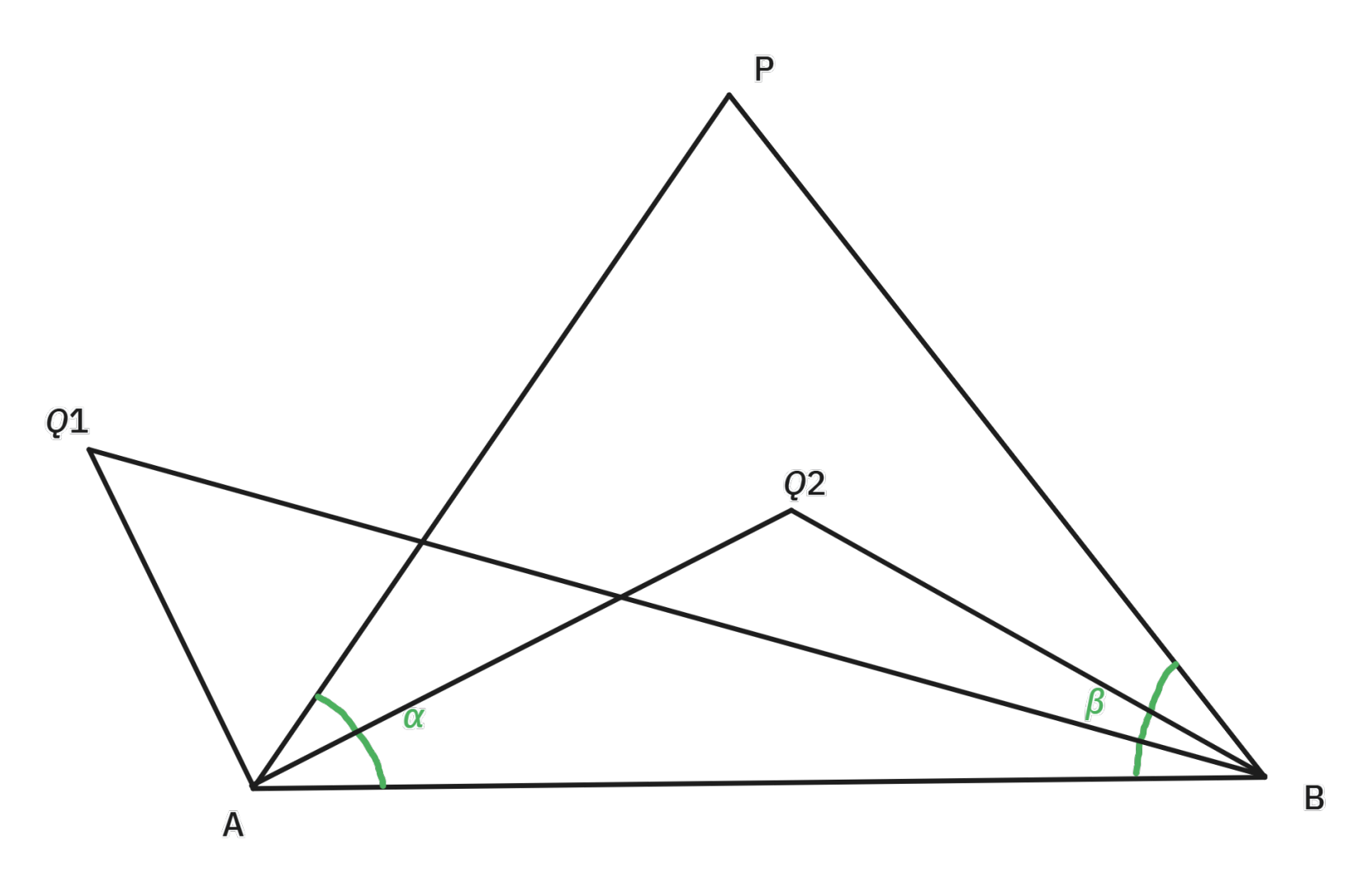
下面只讨论 \(XY\) 一侧的点，设为 \(P_1,P_2,\dots,P_m\)。考虑点 \(P_j\) 在 \(\triangle P_iXY\) 内部的充要条件。对于每个点 \(P_i\)，求出两个角 \(\alpha_i=\angle PXY,\beta_i=\angle PYX\)，得到 \(m\) 对实数二元组 \((\alpha_1,\beta_1),(\alpha_2,\beta_2),\dots,(\alpha_m,\beta_m)\)。由于题目保证不存在三点共线所以 \(\alpha\) 互不相同且均不为 \(0\)，\(\beta\) 同理。则 \(P_j\) 在 \(\triangle P_iXY\) 内部当且仅当 \(\alpha_j<\alpha_i\wedge\beta_j<\beta_i\)。（如上图，\(Q_1\) 不在 \(\triangle PAB\) 内部而 \(Q_2\) 在）。

实数不太方便，考虑离散化，同时不妨设 \(\alpha_1<\alpha_2<\dots<\alpha_m\)，则相当于有一个 \(m\) 阶排列 \(p_{1\sim m}\)，\(P_j\) 在 \(\triangle P_iXY\) 内部当且仅当 \(j<i\wedge p_j<p_i\)。具体在实现过程中，可以对于每个点 \(X\)，将所有其它点 \(Y\) 按照 \(\overrightarrow{XY}\) 的极角进行排序得到循环数组 \(a_{X,1\sim n-1}\)，那么在枚举 \(XY\) 且考虑 \(\overrightarrow{XY}\times\overrightarrow{XP_1}>0\) 的那一侧时，\(P_{1\sim m}\) 一定是 \(Y\) 在 \(a_X\) 中后面紧接着的 \(m\) 个点，也是 \(X\) 在 \(a_Y\) 中前面紧接着的 \(m\) 个点。下图展示了一种 \(m=4\) 时，对于 \(a_X\) 的情况。

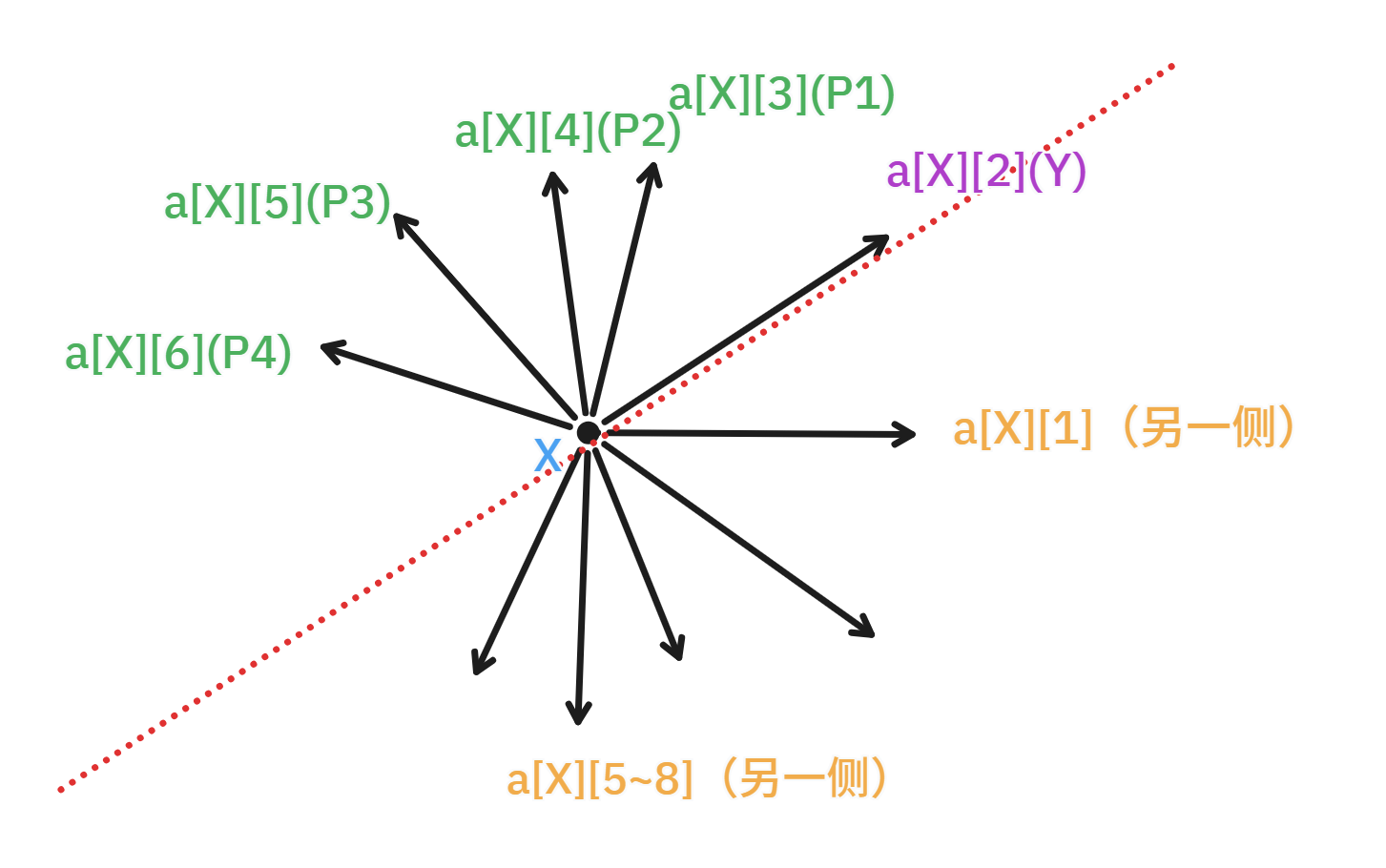
现在问题已经被转化为了序列上的问题。对于内部对角线，要求的就是有多少个 \(i\) 满足 \(\forall j<i,p_j>p_i\)，这是很容易线性求出的。对于外部对角线，要求的就是满足以下条件的 \(i\) 的数量：设下标集合 \(S=\{j|j<i\wedge p_j<p_i\}\)，\(S\) 中最大值为 \(j\)，则 \(p_j=\max_{k\in S}{p_k}\)，也就是 \(S\) 对应的位置中下标最大的和值最大的是同一个。在 \(p\) 上通过单调栈可以线性地求出所有 \(i\) 对应的 \(j\)，在 \(p\) 的逆排列上做一次同样的单调栈即可求出 \(\max_{k\in S}{p_k}\)，检验是否符合要求即可。

预处理极角排序复杂度 \(\mathcal O(n^2\log n)\)，对于每一条对角线 \(XY\) 上述过程都是 \(\mathcal O(n)\) 的，总复杂度 \(\mathcal O(n^3)\)。

参考实现：

#include <bits/stdc++.h>
typedef long long LL;
typedef __int128 LLL;
typedef unsigned long long ULL;
typedef std::pair<int, int> pii;
typedef long double RN;
#define fi first
#define se second
#define MP std::make_pair
#define EB emplace_back

LL read()
{
	LL s = 0; int f = 1, c = getchar();
	for (; !isdigit(c); c = getchar()) f ^= (c == '-');
	for (; isdigit(c); c = getchar()) s = s * 10 + (c ^ 48);
	return f ? s : -s;
}
template<typename T> 
void write(T x, char end = '\n')
{
	if (x < 0) x = -x, putchar('-');
	static int d[100], cur = 0;
	do { d[++cur] = x % 10; } while (x /= 10);
	while (cur) putchar(48 ^ d[cur--]);
	putchar(end);
}
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fll;
template<typename T> void Fmin(T &x, T y){ if (y < x) x = y; }
template<typename T> void Fmax(T &x, T y){ if (x < y) x = y; }
struct Point
{
	int x, y;
	Point(){}
	Point(int _x, int _y) : x(_x), y(_y){}
	friend Point operator+(Point p, Point q){ return Point(p.x + q.x, p.y + q.y); }
	friend Point operator-(Point p, Point q){ return Point(p.x - q.x, p.y - q.y); }
	friend LL operator*(Point p, Point q){ return (LL)p.x * q.y - (LL)p.y * q.x; }
	friend int side(Point p){ if (!p.y) return (p.x > 0 ? 1 : (p.x < 0 ? 2 : 0)); return p.y > 0 ? 1 : 2; }
	friend bool operator<(Point p, Point q)
	{
		int op = side(p), oq = side(q);
		if (op != oq) return op < oq;
		return p * q > 0;
	}
};
const int MAXN = 305;
int n, id[MAXN][MAXN], rk[MAXN][MAXN];
Point p[MAXN];
pii calc(std::vector<pii> vec)
{
	static int a[MAXN], st[MAXN], b[MAXN], lsta[MAXN];
	int m = vec.size(); 
	for (pii p : vec) a[p.fi] = p.se, b[p.se] = p.fi;
	int c1 = 0, c2 = 0, tp = 0, mn = inf;
	st[tp = 0] = 0;
	for (int i = 1; i <= m; i++)
	{
		if (a[i] < mn) mn = a[i], c1++;
		while (tp && a[st[tp]] > a[i]) tp--;
		lsta[i] = st[tp]; st[++tp] = i;
	}
	st[tp = 0] = 0;
	for (int i = 1; i <= m; i++)
	{
		while (tp && st[tp] > b[i]) tp--;
		if (tp && lsta[b[i]] == st[tp]) c2++;
		st[++tp] = b[i];
	}
	return MP(c1, c2);
}
int diff(int x, int i, int j)
{ return (rk[x][j] - rk[x][i] + n - 1) % (n - 1); } 
int calc(int x, int y)
{
	std::vector<pii> Left, Right;
	for (int i = 1; i <= n; i++) if (i != x && i != y)
	{
		if ((p[y] - p[x]) * (p[i] - p[x]) > 0)
			Left.emplace_back(diff(x, y, i), diff(y, i, x));
		else Right.emplace_back(diff(x, i, y), diff(y, x, i));
	}
	pii L = calc(Left), R = calc(Right);
	return L.fi * R.fi + L.se + R.se;
}
int main() 
{
	n = read();
	for (int i = 1; i <= n; i++)
		p[i].x = read(), p[i].y = read();
	for (int i = 1; i <= n; i++)
	{
		int cur = 0;
		for (int j = 1; j <= n; j++) if (i != j) id[i][++cur] = j;
		std::sort(id[i] + 1, id[i] + n, [i](int j, int k){ return (p[j] - p[i]) < (p[k] - p[i]); });
		for (int j = 1; j < n; j++) rk[i][id[i][j]] = j;
	}
	LL ans = 0;
	for (int i = 1; i <= n; i++)
		for (int j = i + 1; j <= n; j++)
			ans += calc(i, j);
	write(ans >> 1);
    return 0;
}