集训队作业2——qoj#1166

Designing a PCB 解题报告

题目大意

平面上有 \(2n\) 个点，第 \(i\) 个位于 \((i-1,0)\)，颜色为 \(a_i\)。保证 \(a_{1\sim 2n}\) 中 \(1\sim n\) 各恰好出现两次。

现在要将每种颜色的一对点用首尾相接且与坐标轴平行的折线连起来，并且任何两种颜色的折线不能有交点。

现在给出 \(n,a_1,a_2,\dots,a_{2n}\)，构造一种连接方案或报告无解。

方案表示方式：对于第 \(i\) 种颜色，输出一行 k[i] c[i][1] d[i][1] c[i][2] d[i][2] ... c[i][k[i]] d[i][k[i]]，其中 \(c_{i,j}\in \{'U','D','L','R'\}\) ，\(d_{i,j}\) 为正整数，表示从颜色 \(i\) 左边那个点开始，依次经过 \(k_i\) 条线段，第 \(i\) 条方向为 \(c_{i,j}\)（UDLR 分别对应上下左右），长度为 \(d_{i,j}\)。

\(2\leq n\leq 1000\)。

解题过程

设颜色 \(i\) 靠左的点编号为 \(l_i\)，靠右的点编号为 \(r_i\)。

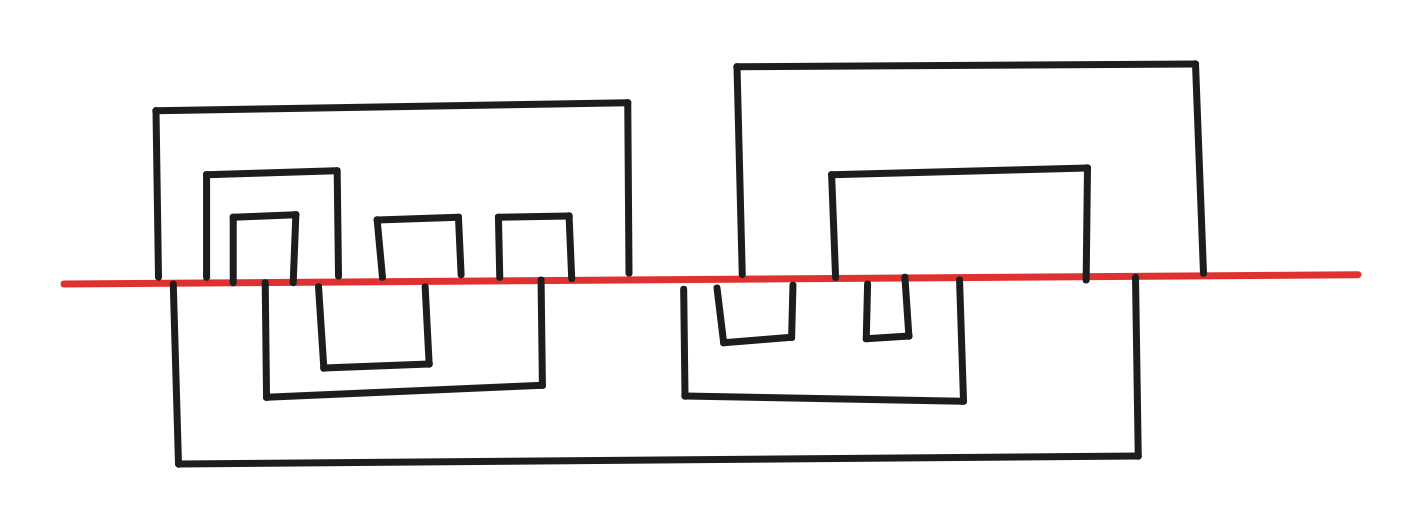
考虑如果折线不能和 \(x\) 轴相交（端点除外），即每条折线要么在 \(x\) 轴上面要么在下面的情况，要如何处理。可以发现如果 \([l_i,r_i]\cap[l_j,r_j]\neq\varnothing\)，那么折线 \(i,j\) 必然处于 \(x\) 轴不同侧。构建一张 \(n\) 个点的图，在所有这样的 \((i,j)\) 之间连边，那么这张图必须是二分图。得到一组二分图染色后，令左部点代表的折线在 \(x\) 轴上方，其余在 \(x\) 轴下方，那么在 \(x\) 轴上方的折线对应的那些 \([l_i,r_i]\) 之间要么相离，要么一个完整包含另一个，所以只需要给每个 \(i\) 赋一个“高度” \(h_i\)，满足如果 \([l_j,r_j]\subset [l_i,r_i]\)，那么 \(h_j<h_i\)，然后将折线 \(i\) 构造为 U h[i] R r[i]-l[i] D h[i]，\(x\) 轴下方也同理。构造 \(h\) 可以直接将所有颜色按 \(r_i-l_i\) 从小到大排序，\(h_i\) 依次为 \(1\sim n\) 即可。

示意图如下：

现在折线可能穿过 \(x\) 轴，意味着每条折线不能简单地归类为上下。但这 \(2n\) 个点可以：定义 \(c_{1\sim 2n}\)，其中 \(c_i=0\) 表示与点 \(i\) 直接相连的线段在 \(x\) 轴上方，反之 \(c_i=1\)。那么可以发现两条限制：

1. 如果 \(l_i<l_j<r_j<r_i\)（即线段包含），那么 \(c_{l_j}=c_{r_j}\)；
2. 如果 \(l_i<l_j<r_i<r_j\)（即线段相交但不包含），那么 \(c_{l_j}\neq c_{r_i}\)。

不难发现这两条限制是必要的。事实上，可以说明这是充分的。

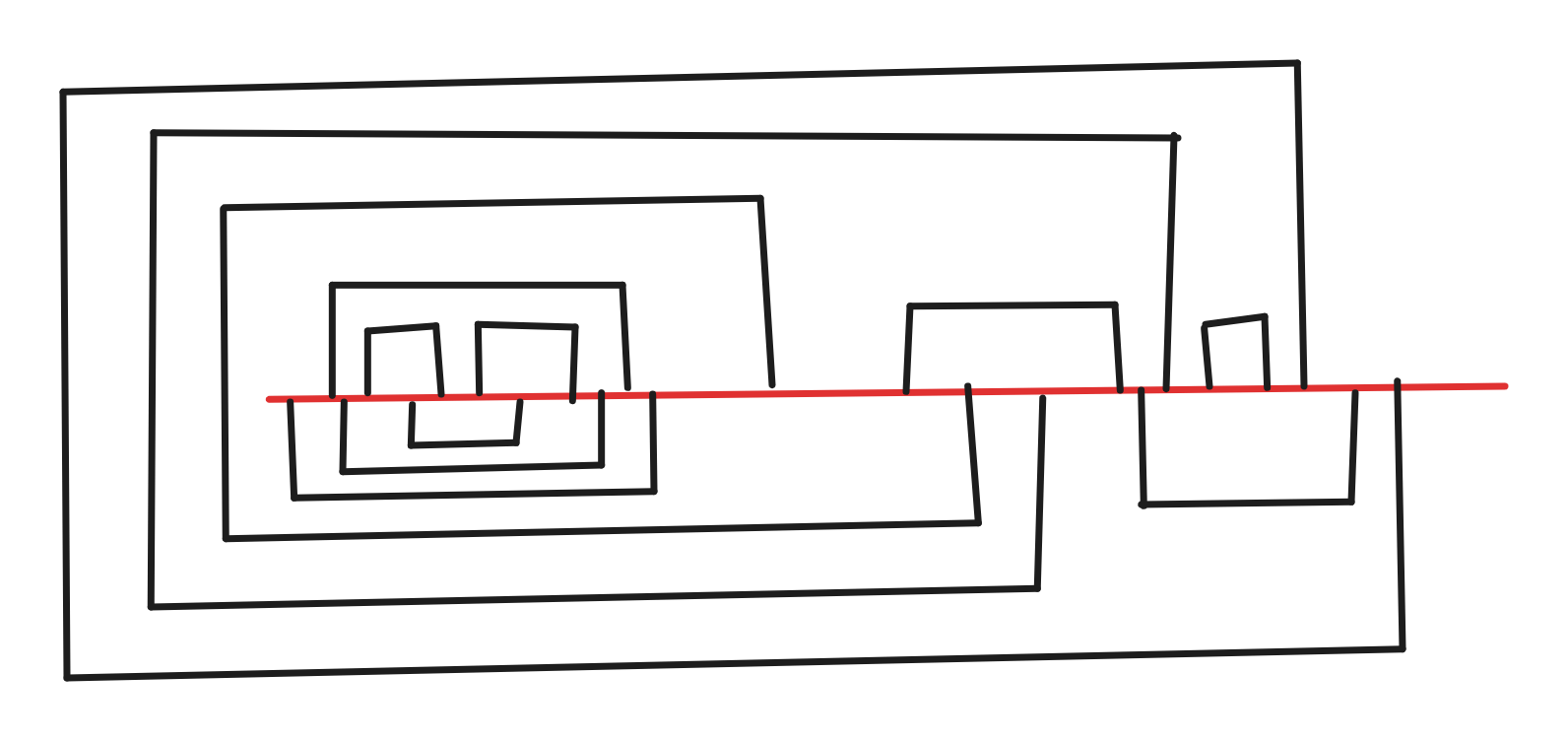
还是缩点后二分图染色得到一组合法的 \(c\)。先像上面的情况一样处理所有 \(c_{l_i}=c_{r_i}\) 的颜色 \(i\)，然后考虑所有 \(c_{l_i}\neq c_{r_i}\) 的颜色 \(i\)。对于这些颜色，再构造一个“宽度” \(w_i\)，满足 \(\forall l_i<l_j\)，有 \(h_i<h_j\) 且 \(w_i < w_j\)，且所有这些颜色的 \(h\) 比所有 \(c_{l_i}=c_{r_i}\) 的 \(h_i\) 大。对于 \(c_{l_i}=0,c_{r_i}=1\) 的 \(i\)，构造折线 U h[i] L l[i]+w[i] D 2*h[i] R r[i]+w[i] U h[i]。\(c_{l_i}=1,c_{r_i}=0\) 的情况同理。

分类讨论可以发现，这样即可保证所有折线不交。

示意图如下：

共有 \(O(n^2)\) 对限制，总复杂度 \(O(n^2)\)。

参考资料

无。