题解：CF1464F My Beautiful Madness

题意简述

给定一棵 \(n\) 个点的树。

对于点 \(u,v\)，定义它们之间的距离 \(dis(u,v)\) 为树上两点间简单路径的边数。

对于点 \(u\)，路径 \(P\)，定义它们之间的距离 \(dis(u,P)=\displaystyle\min_{v\in P}\{dis(u,v)\}\)。

对于路径 \(P,Q\)，定义它们之间的距离 \(dis(P,Q)=\displaystyle\min_{u\in P,v\in Q}\{dis(u,v)\}\)。

现在有一个初始为空的可重路径 \(S\)，有 \(Q\) 次操作，操作共有三种：

1. 往 \(S\) 中加入一条路径 \(P\)。
2. 从 \(S\) 中删除一条路径 \(P\)。
3. 给定 \(d\)，问是否存在点 \(x\)，满足 \(\forall P\in S,dis(x,S)\leq d\)。

另一个版本是只有前两种操作，每次后求出 \(F=\displaystyle\min_x\{\max_{P\in S}\{dis(x,P)\}\)。

前置结论

下面两个做法都要用到一个结论：

• 对于点集 \(S\)，设 \(u,v\in S\) 满足 \(dis(u,v)=\displaystyle\max_{x,y\in S}\{dis(x,y)\}\)，也就是 \(u,v\) 是点集 \(S\) 中距离最远的一对点。那么对于树上任意的点 \(x\)，它到点集
  \(S\) 的最远距离为 \(\displaystyle\max_{y\in S}\{dis(x,y)\}=\max\{dis(x,u),dis(x,v)\}\)。

解法一

求 \(F\) 可以二分转化成 \(\log n\) 次上面的操作 3。

对于路径问题，一个思路是将考虑一条路径变成考虑若干关键点。而一条路径只有一个 \(lca\)，所以考虑 \(lca\) 可能有用。

随便找一个树根，对于点 \(x\) 记其 \(k\) 级祖先为 \(anc(x,k)\)，子树为 \(T_x\)。

考虑操作 3 中什么时候存在满足条件的 \(x\)。对于每条路径 \(P\)，一个必要条件是 \(x\) 要在 \(anc(lca(P),d)\) 的子树中，否则一定有 \(dis(x,P)>d\)。既然是子树限制，那么考虑最深的 \(lca(P)\)，记 \(u=anc(lca(P),d)\)，那么 \(x\) 一定在 \(T_u\) 中。而为了尽可能满足其他路径的限制，\(x=u\) 看起来就很好。事实上，可以证明存在满足条件的 \(x\)，当且仅当 \(u\) 满足条件，证明如下：

1. 显然 \(u\) 满足条件的时候，已经找到满足条件的 \(x\)。
2. 如果 \(u\) 不满足条件，那么存在 \(P\in S\)，使得 \(dis(u,S)>d\)。
3. 如果 \(P\) 与 \(T_u\) 有交，显然 \(P\) 不能经过 \(u\)，所以 \(P\in T_u\)，但由于选的是最深的 \(u\)，此时必然有 \(dis(lca(P),u)\leq d\)，矛盾。
4. 如果 \(P\) 与 \(T_u\) 无交，那么对于任意 \(x\in T_u\)，\(x\) 到 \(P\) 上任意一点的路径都要经过 \(u\)，所以 \(dis(x,P)\geq dis(u,P)\)，故不存在满足条件的 \(x\)。

所以只需要检验 \(u\) 是否合法即可。和上面类似还是考虑 \(v=anc(u,d)\)，那么首先所有路径都要和 \(T_v\) 有交。接下来对路径 \(P\) 的 \(lca\) 分类讨论一下：

1. 如果 \(lca(P)\in T_u\)，这个上面讨论过了，一定有 \(dis(u,P)\leq d\)。
2. 如果 \(lca(P)\) 在路径 \((u,v)\) 上，那么 \(dis(u,P)\leq dis(u,lca(P))\leq dis(u,v)\leq d\)。
3. 如果 \(lca(P)\notin T_v\)，由于 \(P\) 和 \(T_v\) 有交，所以 \(P\) 经过 \(v\)，也有 \(dis(u,P)\leq d\)。
4. 否则，\(lca(P)\) 和 \(u\) 没有祖先后代关系，此时有 \(dis(u,P)=dis(u,lca(P))\)，故条件等价于 \(dis(u,lca(P))\leq d\)。

可以发现，对于前两种情况，也一定有 \(dis(u,lca(P))\leq d\)，所以可以将条件转化为：

1. \(\forall P\in S,P\cap T_v\neq \empty\)。
2. \(\forall P\in S\wedge lca(P)\in T_v,dis(u,lca(P))\leq d\)。

对于第一个条件，可以用树状数组维护树上差分解决。

对于第二个条件，实际上是要 \(u\) 到所有在 \(v\) 的子树内的 \(lca(P)\) 的距离最大值。这就是前置结论中的问题，线段树维护点集直径即可。

树剖求 \(lca\) 可以做到 \(O(n+Q\log^2n)\)，转 \(\mathrm{RMQ}\) 用 st 表可以做到 \(O(n\log n+Q\log n)\)。

求 \(F\) 则是 \(O(n+Q\log^3n)\) 或 \(O(n\log n+Q\log^2n)\)。

提交记录（st 表和树剖差不多）。

解法二

上面的解法中我们将求 \(F\) 通过二分转化为操作 3，现在反过来，求出 \(F\) 后和 \(d\) 比较来回答操作 3。

考虑一个特殊情况：所有路径都是单点。此时路径集 \(S\) 变成了点集，那么就是求 \(F=\displaystyle\min_x\{\max_{u\in S}\{dis(x,u)\}\)。对于每个 \(x\)，要求它到点集 \(S\) 的最大距离，那么由前置结论，求出 \(S\) 的直径 \((u,v)\)，就有 \(F=\displaystyle\min_x\{\max\{dis(x,u),dis(x,v)\}\)。对于所有 \(x\) 求最小值，那么取到最小的 \(x\) 就应该是 \((u,v)\) 路径的中点，故 \(F=\lceil\frac{dis(u,v)}{2}\rceil\)。

现在 \(S\) 中不是点而是路径，有什么区别呢？可以大胆猜想没有什么区别，记路径集直径 \(D(S)=\displaystyle\max_{P,Q\in S}\{dis(P,Q)\}\)，则 \(F=\lceil\frac{D(S)}{2}\rceil\)。

设 \(S\) 中距离最远的两条路径是 \(P,Q\)，那么要证明上面这个结论，我们证明对于任意的点 \(x\)，\(x\) 到 \(S\) 中路径的最远距离是：

\[\begin{cases} \max\{dis(x,P),dis(x,Q)\}, &D(S)>0\\ dis(x,\bigcap_{p\in S}p), &D(S)=0 \end{cases} \]

即在 \(D(S)>0\) 时只需要考虑最远的两条路径，在 \(D(S)=0\) 时只需要考虑所有路径的交（此时这个交一定非空）。

先证明 \(D(S)>0\) 的情况，假设存在路径 \(R\)，满足 \(dis(x,R)>dis(x,P),dis(x,Q)\)，将路径 \(R\) 作为树根，其他部分会形成若干子树，显然 \(x\) 不在 \(R\) 上，不妨 设 \(x\) 在子树 \(u\) 中，与 \(u\) 相邻的 \(R\) 上的点是 \(f\)，则 \(dis(x,R)=dis(x,f)\)。如下图：

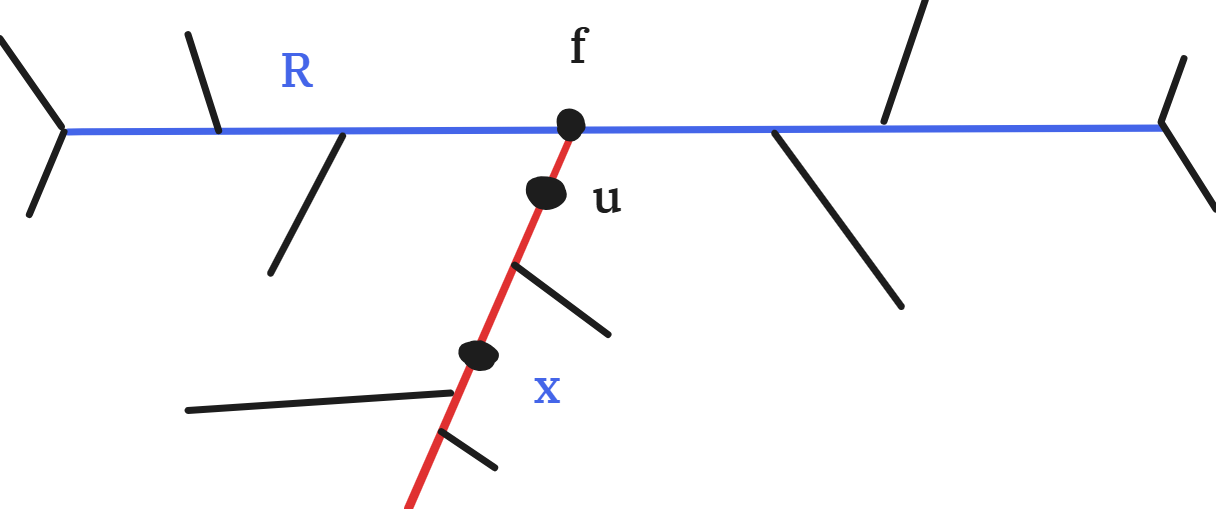
接下来分类讨论有点多，建议画一张这种图以更好地理解：

1. 若 \(P,Q\) 中至少一条与子树 \(u\) 无交（不妨设为 \(P\)），那么从 \(x\) 到 \(P\) 上任何一点都要经过 \((u,f)\) 这条边，所以 \(dis(x,P)\geq dis(x,f)\)，矛盾；
2. 若 \(P,Q\) 中至少一条经过 \(u\)（不妨设为 \(P\)），那么显然 \(Q\) 不经过 \(u\)，所以 \(Q\) 在 \(u\) 子树内，此时 \(dis(R,Q)=dis(f,Q)>dis(u,Q)\geq dis(P,Q)\)，矛盾。
3. 对于下面的几种情况，\(P,Q\) 都在 \(u\) 子树内，所以 \(dis(P,R)=dis(lca(P),f),dis(Q,R)=dis(lca(Q),f)\)。方便起见，记 \(p=lca(P),q=lca(Q)\)。
   1. 若 \(p,q\) 存在祖先后代关系（不妨设 \(p\) 是祖先），那么有 \(dis(f,q)>dis(p,q)\geq dis(P,Q)\)，矛盾；
   2. 当 \(p,q\) 不存在祖先后代关系时，有 \(dis(P,Q)=dis(p,q)\)。
      1. 若 \(P,Q\) 中有一个与路径 \((x,u)\) 有交（不妨设为 \(P\)），那么 \(Q\) 肯定与 \((x,u)\) 无交（否则会变成情况 4），那么此时 \(q\) 为 \(x\) 的后代或者没有祖先后代关系，所以有 \(dis(x,Q)=dis(x,q)\)，且 \(dis(x,P)\leq dis(x,p)<dis(x,f)\)。
         • 这时候考察点 \(x\) 和点集 \({f,p,q}\)，由 \(dis(P,Q)\geq dis(P,R),dis(Q,R)\)，得 \(dis(p,q)\geq dis(p,f),dis(q,f)\)。
         • 那么由点到点集的最远距离的结论，有 \(\max\{dis(x,p),dis(x,q)\}\geq dis(x,f)\)，这与 \(\max\{dis(x,P),dis(x,Q)\}\geq dis(x,R)\) 矛盾。
      2. 若 \(P,Q\) 均和 \((x,u)\) 无交，那么和上面类似有 \(dis(x,P)=dis(x,p),dis(x,Q)=dis(x,q)\)，会导出一样的矛盾。

上面的讨论覆盖了所有情况，故这部分得证。

对于 \(D(S)=0\) 的情况，可以归纳变成只有两条路径的情况，设为 \(P,Q\)，记 \(R=P\cap Q\)。如下图：

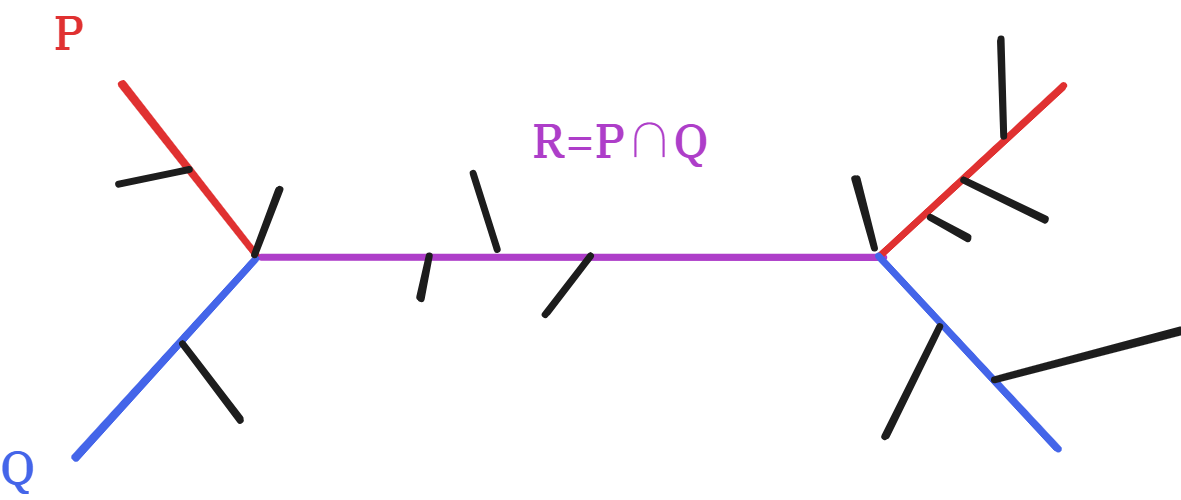
可以发现本质上 \(x\) 所在的子树只有三种不同情况：接在 \(P\setminus R\) 上、接在 \(Q\setminus R\) 上、接在 \(R\) 上。分别讨论不难证明。

剩下的问题就是要维护最远的 \(P,Q\) 或所有路径的交。求出两条路径的距离或者交可以根据四个端点两两的 \(lca\) 分类讨论得到。对于路径之间的距离，有和上面类似的结论：任意的路径 \(p\)，\(p\) 到 \(S\) 中路径的最远距离是：

\[\begin{cases} \max\{dis(p,P),dis(p,Q)\}, &D(S)>0\\ dis(p,\bigcap_{q\in S}q), &D(S)=0 \end{cases} \]

证明也差不多。所以可以类似线段树维护点集直径用线段树维护路径集直径。

用 st 表求 \(lca\) 复杂度 \(O((n+Q)\log n)\)。

求 \(F\) 比较有优势，在这个题上没有。

提交记录。