题解：P14309 【MX-S8-T2】配对

树上两种点权为 \(1/0\) 的点可以用黑白颜色区分。

单次匹配中，选定的两个黑点之间路径上不能再包含其它的黑点了。如图所示，如果不这样的话，之后中间的黑点与其它的黑点匹配时，蓝色段的代价会被重复统计，这是不优的，对吧？

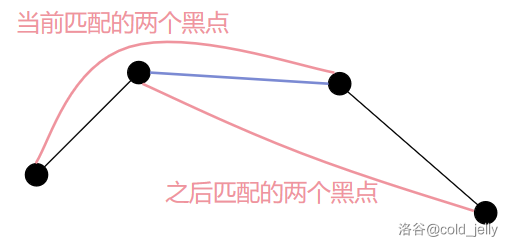
我们尽可能地要让相邻的两个黑点匹配：

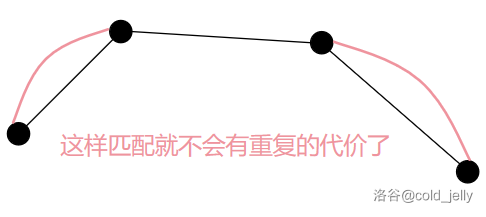
放到树上去，上面这个结论其实说明了对于每个子树中的所有黑点都应该尽可能进行内部匹配，最多剩下一个黑点没有匹配（这种情况说明子树内黑点个数为奇数）。因为如果剩下的黑点数超过 \(1\) 时，这些黑点与子树外的黑点匹配时，都会重复统计 LCA 往上的一段路径代价：

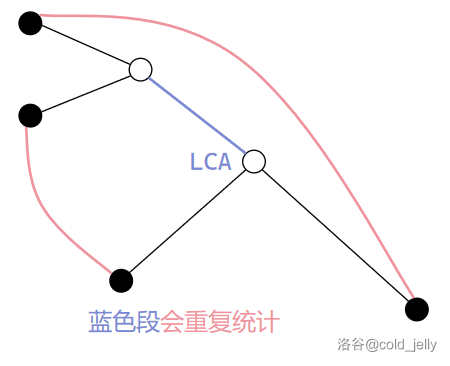
我们现在关心的是子树内黑点个数的奇偶性，但是奇偶性是会改变的。题目中的交换操作会造成什么影响呢？首先如果两点权值相同则无影响，然后权值不同的话就相当于将两个点的颜色取反，对吧。

不止交换会导致奇偶性改变。我们考虑如果黑点的个数为奇数时，匹配到最后是会剩一个的，那么这个黑点相当于白点，同样是一个取反的操作。

也就是说，会改变奇偶性的操作可以归纳为颜色取反的操作，且黑点最多会被取反 \(2\) 个，白点最多会被取反 \(1\) 个。

因此我们可以考虑按照取反的点的个数设计状态。设计 \(f(u,x,y)\) 表示 \(u\) 子树内取反了 \(x\in[0,2]\) 个黑点、\(y\in[0,1]\) 个白点的最小代价。

对于转移，需要枚举当前节点 \(u\) 以及子节点 \(v\) 的 \(x,y\) 值（分别为 \(x_1,y_1\) 和 \(x_2,y_2\)），合并状态时，我们临时存储 \(g\) 表示更新后的状态。那么有方程：

\[g(x,y)=\left\{\begin{matrix} \min\{g(x,y),f(u,x_1,y_1)+f(v,x_2,y_2)\} & t\equiv 0\pmod 2\\ \min\{g(x,y),f(u,x_1,y_1)+f(v,x_2,y_2)+w(u,v)\} & t\equiv 1\pmod 2 \end{matrix}\right. \]

其中 \(t\) 表示 \(v\) 子树内黑点的个数，其等于原始黑点数量加上 \(x_2+y_2\)。而仅当 \(t\) 为奇数时，才会记录一次 \(w(u,v)\) 的代价。

如果整棵树中黑点个数为偶数，那么答案为 \(\min\{f(1,0,0),f(1,1,1)\}\)；否则答案为 \(\min\{f(1,1,0),f(1,2,1)\}\)。

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1e6 + 10;

int n;
bool c[N];
int h[N], e[N * 2], ne[N * 2], w[N * 2], idx;

void add(int x, int y, int z)
{
	e[idx] = y, ne[idx] = h[x], w[idx] = z, h[x] = idx ++;
}

int dep[N], fa[N], siz[N];//siz：原始黑点个数 

void dfs1(int u, int father)
{
	dep[u] = dep[father] + 1;
	fa[u] = father;
	siz[u] = c[u]; 
	
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i];
		
		if(v == father)
		{
			continue;
		}
		
		dfs1(v, u);
		siz[u] += siz[v];
	}
}

int f[N][4][3], g[4][3];
int x[3], y[3];

void dfs2(int u)
{
	f[u][0][0] = 0;
	
	if(c[u])
	{
		f[u][1][0] = 0;
	}
	else
	{
		f[u][0][1] = 0;
	}
	
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i], W = w[i];
		
		if(v == fa[u])
		{
			continue;
		}
		
		dfs2(v);
		
		memset(g, 0x3f, sizeof g);
		
//		枚举 u, v 的 x, y 值，统计答案 
		for(x[1] = 0; x[1] <= 2; x[1] ++)
		{
			for(y[1] = 0; y[1] <= 1; y[1] ++)
			{
				for(x[2] = 0; x[2] <= 2; x[2] ++)
				{
					for(y[2] = 0; y[2] <= 1; y[2] ++)
					{
						int X = x[1] + x[2], Y = y[1] + y[2];//合并后的 x, y 值 
						
						if(X > 2 || Y > 1)//不满足限制 
						{
							continue;
						}
						
						if((siz[v] + x[2] + y[2]) & 1)
						{
							g[X][Y] = min(g[X][Y], f[u][x[1]][y[1]] + f[v][x[2]][y[2]] + W);
						}
						else
						{
							g[X][Y] = min(g[X][Y], f[u][x[1]][y[1]] + f[v][x[2]][y[2]]);
						}
					}
				}
			}
		}
		
		memcpy(f[u], g, sizeof g);
	}
}

signed main()
{
//	freopen("match.in", "r", stdin);
//	freopen("match.out", "w", stdout);
	
	memset(h, -1, sizeof h);
	memset(f, 0x3f, sizeof f);
	
	cin >> n;
	
	for(int i = 1; i <= n; i ++)
	{
		scanf("%d", &c[i]);
	}
	
	for(int i = 1; i < n; i ++)
	{
		int x, y, z;
		
		scanf("%lld%lld%lld", &x, &y, &z);
		
		add(x, y, z), add(y, x, z);
	}
	
	dfs1(1, 0);
	dfs2(1);
	
	if(siz[1] & 1)
	{
		cout << min(f[1][1][0], f[1][2][1]);
	}
	else
	{
		cout << min(f[1][0][0], f[1][1][1]);
	}
	
	return 0;
}