模拟退火

模拟退火是一种通过随机化算法得出一类题目的最优方案的算法。

模拟退火时，如果当前状态比目前最优解更优则更新最优解，否则概率接受该状态（而不是直接将该状态给不人性化地 pass 掉），这个概率会不断减小，直到最后找到最优解。

为什么要这样做呢？对于这类最优化问题，我们如果把所有可能的状态集合的解给排成一列，那么会得到一个答案关于状态的一个函数 \(f(S)\)：

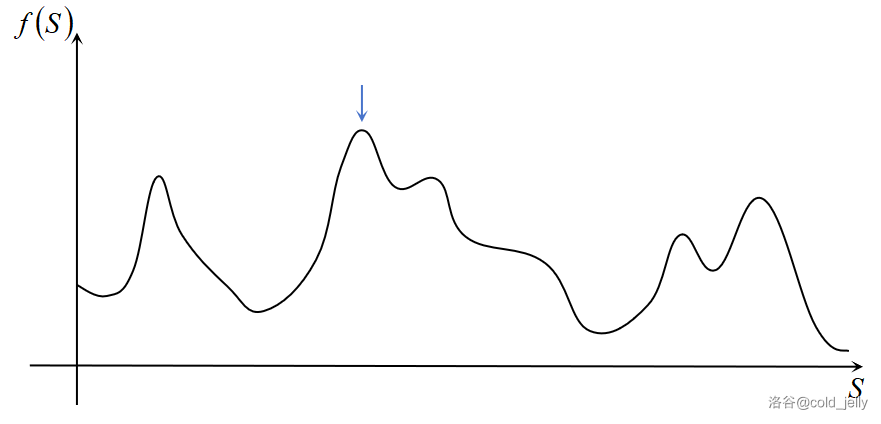
很明显其不一定是一个单峰函数，因此爬山算法不可行，而如果我们不概率接受看起来更劣的状态，那么就会拘泥于一个山峰而不能看到更远的更高的山峰。

模拟退火算法需要借助几个参数实现：初始温度 \(T_0\)，终止温度 \(T_e\)，降温系数 \(d\)。其中 \(T_0\) 为较大正数（一般在 \(10^3\) 及以上级别），\(T_e\) 为较小正数（一般在 \(10^{-15}\) 左右的级别），\(d\) 为一个接近 \(1\) 的实数（一般取 \(0.9\sim 1\) 中的数）。

退火前，让当前温度 \(T=T_0\)。然后尝试随机扰动转换到另一个状态，如果该状态的答案比当前最优解更优则更新最优解，否则以 \(P=\exp\left ( -\dfrac{\Delta ans}{T} \right )\) 的概率更改状态，其中 \(\Delta ans\) 为当前最优解答案与该状态答案的差值。更改完状态后，让温度 \(T\) 乘以 \(d\)（降温）。重复操作直到 \(T\le T_e\)。

例题：P3878 [TJOI2010] 分金币。

#include<bits/stdc++.h>

using namespace std;

const int N = 35, INF = INT_MAX;

int T, n, tpans, ans;
int a[N];

double Rand()
{
	return (double)rand() / RAND_MAX;
}

void work()
{
	int ans1 = 0, ans2 = 0;
	
	for(int i = 1; i <= (n + 1) / 2; i ++)
	{
		ans1 += a[i];
	}
	
	for(int i = (n + 1) / 2 + 1; i <= n; i ++)
	{
		ans2 += a[i];
	}
	
	tpans = abs(ans1 - ans2);
}

void SA()//模拟退火 
{
	double T, T0 = 2500, d = 0.985, Te = 1e-15;
	
	T = T0;
	
	while(T > Te)
	{
		int x = rand() % n + 1;
		int y = rand() % n + 1;
		
		swap(a[x], a[y]);
		
		work();
		
		if(tpans < ans)
		{
			ans = tpans;
		}
		else if(exp((double)(ans - tpans) / T) < Rand())
		{
			swap(a[x], a[y]);
		}
		
		T *= d;
	}
}

void solve()
{
	cin >> n;
	
	for(int i = 1; i <= n; i ++)
	{
		scanf("%d", &a[i]);
	}
	
	ans = INF;
	
	for(int i = 1; i <= 100; i ++)
	{
		SA();
	}
	
	cout << ans << "\n";
}

int main()
{
	srand(time(0));
	
	cin >> T;
	
	while(T --)
	{
		solve();
	}
	
	return 0;
}

习题

posted @ 2025-10-29 21:42  cold_jelly  阅读(8)  评论(0)    收藏  举报