【圆方树】学习笔记

前置知识：点双连通分量。

---

圆方树的构建

圆方树是一种将图变成树的方法。

顾名思义，圆方树上的节点分为圆点和方点两种。其中圆点为原图中的节点，而方点是每个 v-DCC 缩点后得到的点。因此若原图包含 \(n\) 个节点以及 \(s\) 个 v-DCC，那么构建出来的圆方树就包含 \(n+s\) 个节点。

而圆方树的建边方式为：将每个方点与属于该 v-DCC 的节点对应的圆点连边。什么意思呢？我们看下面的图：

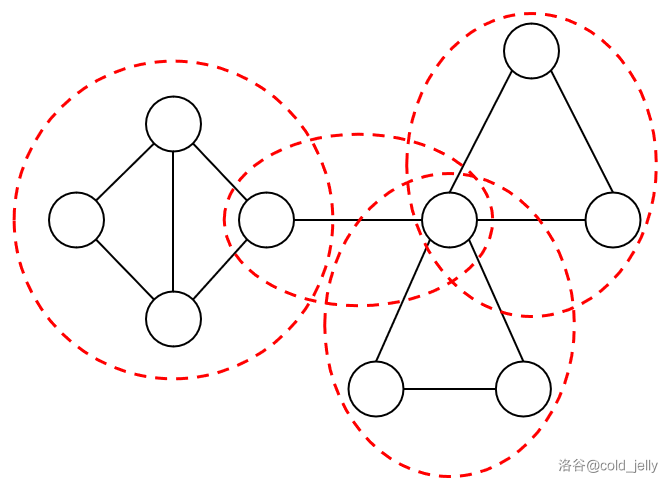
我用红色椭圆圈住了 \(4\) 个 v-DCC，那么我们新开 \(4\) 个方点代表每个 v-DCC：

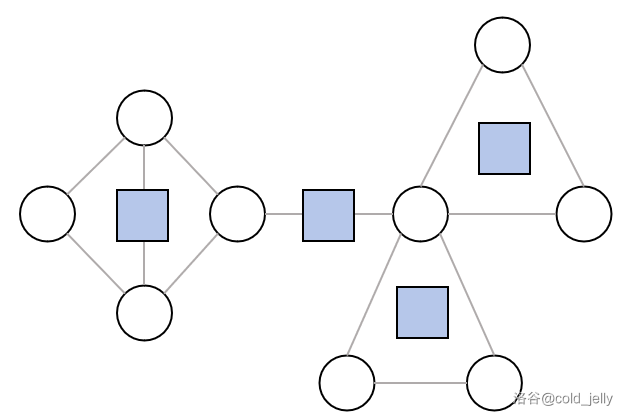
我们再用上面的连边方式给圆点和方点之间连边：

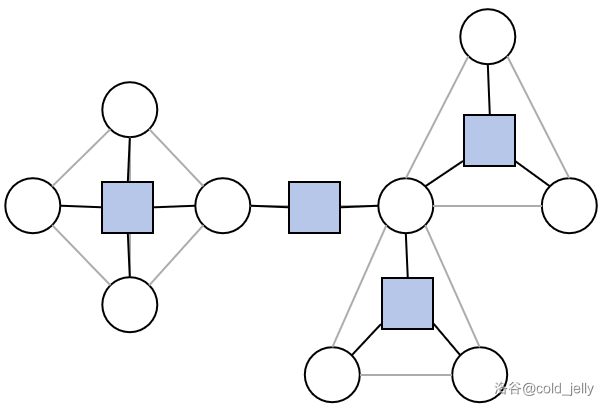
最终圆点和方点以及所有新建出来的边共同构成了原图的圆方树。

通过上述方式建出的圆方树有如下性质：

1. 若原图不连通，则建出来的是圆方树森林，并且原图连通的两点在圆方树上也连通；
2. 相邻的点的形状一定不同；
3. 所有度数 \(>1\) 的圆点在原图中一定是割点；
4. 方点的度数是 v-DCC 的大小。

由于要用到 v-DCC，我们首先用 Tarjan 算法求出每个点属于的 v-DCC 颜色，我们在初始化时令 vDCC = n：

void tarjan(int u)
{
	dfn[u] = low[u] = ++ idx;
	s.push(u);
	if(u == root && h[u] == -1)
	{
		belong[u].push_back(++ vDCC);
		return;
	}
	int cnt = 0;
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if(dfn[u] <= low[v])
			{
				cnt ++;
				if(u != root || cnt > 1) cut[u] = true;
				vDCC ++;
				int top;
				do
				{
					top = s.top();
					s.pop();
					belong[top].push_back(vDCC);
				}while(top != v);
				belong[u].push_back(vDCC);
			}
		}
		else low[u] = min(low[u], dfn[v]);
	}
}

然后我们建立一张新图，用来存储圆方树的信息。具体来说，我们对于每个节点，将它与其所属的 v-DCC 的颜色相连。

	for(int i = 1; i <= n; i ++)
		for(auto j : belong[i])
		{
			e2[i].push_back(j);
			e2[j].push_back(i);
		}

注意，因为圆方树中我们新开了方点，而无向图中 v-DCC 的数量是 \(\le n\) 的，因此代码中各个数组大小都应该开两倍。

圆方树的应用

通过圆方树，我们将图变成了树，从而很方便地支持我们做很多树上操作（例如树链剖分、树形 DP 等等）了。

例题：P4630 [APIO2018] 铁人两项：给定一张无向图，要求满足能从 \(s\) 出发，经过 \(c\)，最终到达 \(f\) 的三元组 \((s,c,f)\) 的数量。

我们首先把每个 v-DCC 缩点，然后建成圆方树。

我们考虑如何在圆方树上对应合法的三元组 \((s,c,f)\)。如果 \(s\) 和 \(f\) 属于同一个 v-DCC，那么该 v-DCC 中除 \(s\) 和 \(f\) 的其余点都可以作为中转点 \(c\)；否则 \(s\) 和 \(f\) 不属于同一个 v-DCC，放在圆方树上，即就是在两个不同方点上，此时我们统计树上两个方点之间的唯一路径，路径上所有 v-DCC 内的每一个点都可以作为中转点 \(c\)。

我们发现这里可以枚举 \(c\)，然后求其对应的合法的 \((s,c,f)\) 的数量。

做法一：

设 \(f_i\) 表示以 \(i\) 为根的子树内有多少个点对 \((u,v)\) 满足 \((u,i,v)\) 合法，设 \(siz_i\) 表示以 \(i\) 为根的子树大小（只算圆点，不算方点），设 \(d_i\) 表示当 \(i\) 为方点时该 v-DCC 的大小（即点 \(i\) 的度数），我们根据点 \(i\) 的形状分类讨论：

• 若 \(i\) 为圆点，那么我们考虑 \(i\) 的每个子树上的每一个点都能经过 \(i\) 到达剩余子树的每一个点上，由乘法原理得：\(\displaystyle f_i=\sum_{j=son_i}siz_j\times(siz_i-siz_j-1)\)；
• 若 \(i\) 为方点，那么在 \(i\) 为圆点的基础上，这个方点内的所有点都可作为中转点，因此我们有：\(\displaystyle f_i=(d_i-2)\times \sum_{j=son_i}siz_j\times(siz_i-siz_j)\)。

我们此时可以枚举圆方树的树根跑 DP，复杂度为 \(O(n^2)\)。可以用换根 DP 做到 \(O(n)\)。

做法二：

我们可以发现，我们如果枚举点 \(i\)，合法的 \((s,c,f)\) 有另一种方法算，我们可以计算 \(i\) 往下的下一级的各个子树的大小乘积，再乘上 \(i\) 对应的 v-DCC 的大小（如果 \(i\) 是方点的话）。

但是这样会算重，因为割点被重复统计了。那么我们考虑容斥，在最后统计答案时将经过割点的答案扣掉即可。

这里有个小 Trick，我们可以设一个点权帮助计算，令方点的点权为 v-DCC 的大小，而令圆点的点权为 \(-1\)，这样就可以统计圆方树上两圆点间路径的点权和了。给圆方树上的点赋点权是应用圆方树解题的一种经典思路，具体问题具体分析。

这里给出做法二的代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10, M = 4e5 + 10;//注意 2 倍 
int n, m, ans = 0;
int h[N], e[M], ne[M], ide;
void add(int u, int v)
{
	e[ide] = v, ne[ide] = h[u], h[u] = ide ++;
}
int root;
int dfn[N], low[N], idx;
stack<int> s;
bool cut[N];
vector<int> belong[N];
int vDCC;
int w[N];//点权 
int SIZ, Siz[N], siz[N];
void tarjan(int u)
{
	dfn[u] = low[u] = ++ idx;
	s.push(u);
	SIZ ++;
	if(u == root && h[u] == -1)
	{
		belong[u].push_back(++ vDCC);
		return;
	}
	int cnt = 0;
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if(dfn[u] <= low[v])
			{
				cnt ++;
				if(u != root || cnt > 1) cut[u] = true;
				vDCC ++;
				w[vDCC] = 0;
				int top;
				do
				{
					top = s.top();
					s.pop();
					belong[top].push_back(vDCC);
					w[vDCC] ++;
				}while(top != v);
				belong[u].push_back(vDCC);
				w[vDCC] ++;
			}
		}
		else low[u] = min(low[u], dfn[v]);
	}
}
vector<int> e2[N];//新图 
vector<int> start;
void dfs(int u, int father)
{
	if(u <= n) siz[u] = 1;//方点不计 siz 
	for(auto v : e2[u])
	{
		if(v == father) continue;
		dfs(v, u);
		ans += 2 * w[u] * siz[u] * siz[v];
		siz[u] += siz[v];
	}
	ans += 2 * w[u] * siz[u] * (Siz[root] - siz[u]);//不能写 (n - siz[u])，图不连通 
}
signed main()
{
	memset(h, -1, sizeof h);
	memset(w, -1, sizeof w);
	cin >> n >> m;
	vDCC = n;
	for(int i = 1; i <= m; i ++)
	{
		int u, v;
		scanf("%lld%lld", &u, &v);
		add(u, v), add(v, u);
	}
	for(int i = 1; i <= n; i ++)
		if(!dfn[i])
		{
			root = i;
			SIZ = 0;
			start.push_back(i);
			tarjan(i);
			Siz[i] = SIZ;
		}
	for(int i = 1; i <= n; i ++)
		for(auto j : belong[i])
		{
			e2[i].push_back(j);
			e2[j].push_back(i);
		}
	for(auto i : start)
	{
		root = i;
		dfs(i, -1);
	}
	cout << ans;
	return 0;
}