【图论】总结 9：点双连通分量

点双连通分量（v-DCC）是另一种无向图的双连通分量。

---

无向图的割点与 v-DCC

对于一张连通的无向图，如果我们将其中一个点及其关联边删去，将会将无向图分裂为若干连通块，那么我们称这条边为无向图的割点。例如下图展示了一个无向图的所有割点：

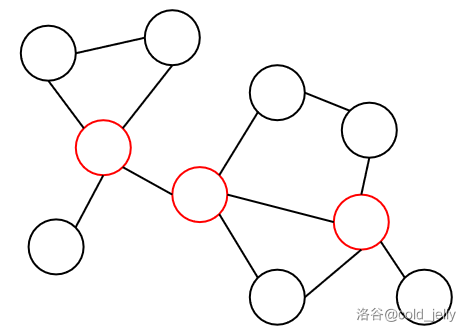
下图演示了将其中一个割点及其关联边删去后得到的连通块：

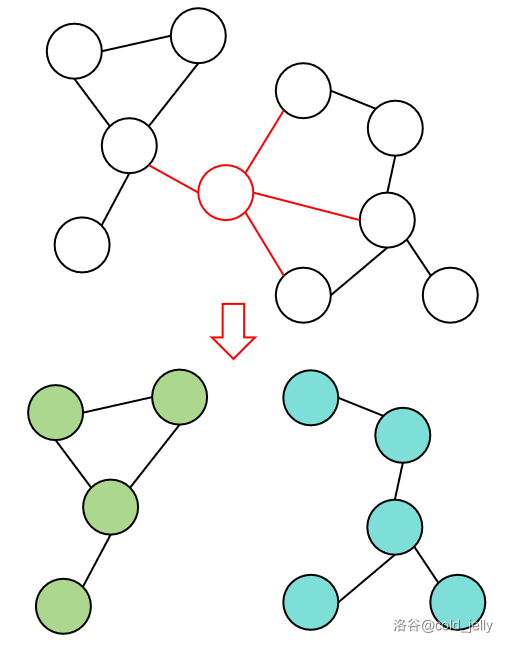
而对于一个连通图，如果其不存在割点，我们称其是点双连通图。无向图中极大的点双连通子图被称为无向图的点双连通分量（v-DCC）。例如下图每个虚线框为一个点双连通分量（图有点乱，要仔细看）：

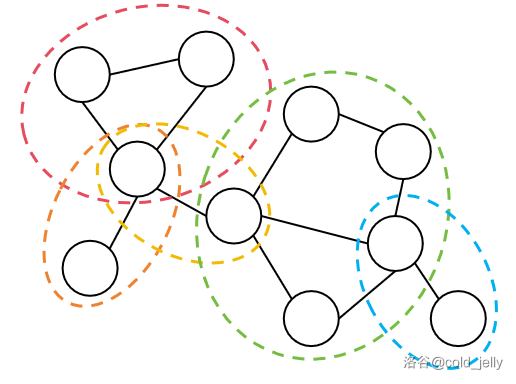
Tarjan 算法求割点

类似于有向图中求 SCC 的过程，我们定义每个节点 \(u\) 的时间戳 \(dfn[u]\) 与追溯值 \(low[u]\)：

\(dfn[u]\)：对于无向图，在 DFS 形成搜索树的过程中按照节点第一次被遍历到的先后顺序给节点赋予 \(1\sim n\) 的整数标记，该标记即为 \(dfn[u]\)；
\(low[u]\)：是满足以下任意一条的所有节点中时间戳的最小值：（1）搜索树上 \(\text{SubTree}(u)\) 中的节点；（2）通过 \(1\) 条不在搜索树上的边，能到达 \(\text{SubTree}(u)\) 上的节点。

这个定义与求割边过程中所用到的定义是完全相同的。

利用 \(dfn\) 数组以及 \(low\) 数组，我们可以得出：

若 \(u\) 不是搜索树的根节点，则 \(u\) 是割点当且仅当搜索树上存在 \(u\) 的一个子节点 \(v\)，满足 \(dfn[u]\le low[v]\)；若 \(u\) 是搜索树的根节点，那么 \(u\) 是割点当且仅当搜索树上存在至少两个 \(u\) 的子节点 \(v_1,v_2\)，它们满足 \(\left\{\begin{matrix} dfn[u]\le low[v_1] \\ dfn[u]\le low[v_2] \end{matrix}\right.\)。

Tarjan 算法利用了这个结论，可在 \(O(n+m)\) 的时间复杂度内求得无向图的所有割点。我们以一个例子过一遍 Tarjan 算法的流程。例图如下（节点内为时间戳，蓝色数字为追溯值，绿色粗边为树枝边）：

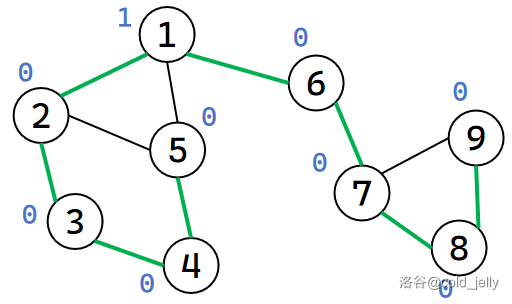
初始时首先遍历到 \(1\) 号节点，此时 idx ++（\(idx=1\)）并赋值给 \(dfn[1]\) 和 \(low[1]\)。

接下来遍历到 \(2\) 号节点，此时 idx ++（\(idx=2\)）并赋值给 \(dfn[2]\) 和 \(low[2]\)。

以此类推遍历到 \(5\) 号节点，此时 idx ++（\(idx=5\)）并赋值给 \(dfn[5]\) 和 \(low[5]\)，此时情景如下：

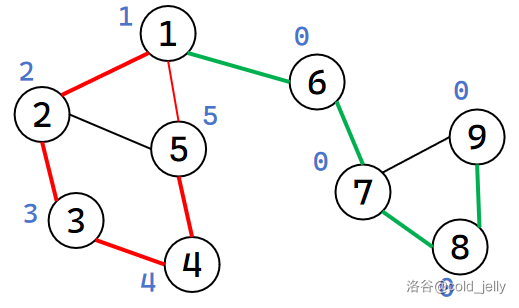
接下来遍历到 \(1\) 号节点，发现 \(1\) 号节点已被遍历，所以令 \(low[5]=\min\{low[5],dfn[1]\}=1\)，这一步与求 e-DCC 同。

同理继续扫描 \(5\) 号节点的其它出边，扫描到 \(2\)，令 \(low[5]=\min\{low[5],dfn[2]\}=1\)。

\(5\) 号节点没有出边了，回溯到 \(4\)，更新 \(low[4]=\min\{low[4],low[5]\}=1\)；

继续回溯到 \(3\)，更新 \(low[3]=\min\{low[3],low[4]\}=1\)；

继续回溯到 \(2\)，更新 \(low[2]=\min\{low[2],low[3]\}=1\)；

继续回溯到 \(1\)，更新 \(low[1]=\min\{low[1],low[2]\}=1\)，并发现 \(dfn[1]\le low[2]\)。我们在一开始时记录一个数 \(cnt\)，表示搜索树上满足上面的 \(dfn[u]\le low[v]\) 条件的子树数量，那么此时我们将 cnt ++（\(cnt=1\)）。然后我们判定 \(1\) 是否为搜索树的根节点，发现是，并且此时 \(cnt>0\)，那么我们根据割点判定法则，认定 \(1\) 为割点并标记。

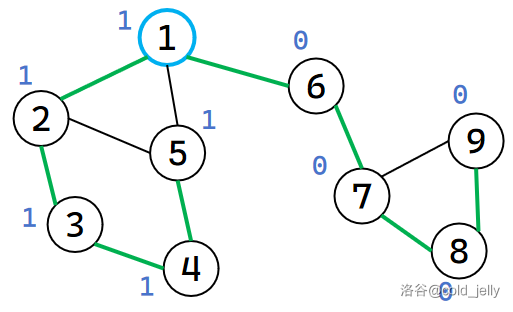
接下来继续扫描 \(1\) 的出边，跳过 \(5\)，访问到 \(6\)，此时 idx ++（\(idx=6\)）并赋值给 \(dfn[6]\) 和 \(low[6]\)：

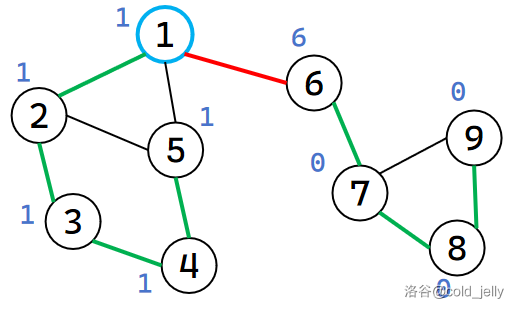
接下来遍历到 \(7\)，此时 idx ++（\(idx=7\)）并赋值给 \(dfn[7]\) 和 \(low[7]\)。

以此类推遍历到 \(9\)，此时 idx ++（\(idx=9\)）并赋值给 \(dfn[9]\) 和 \(low[9]\)，场景如下：

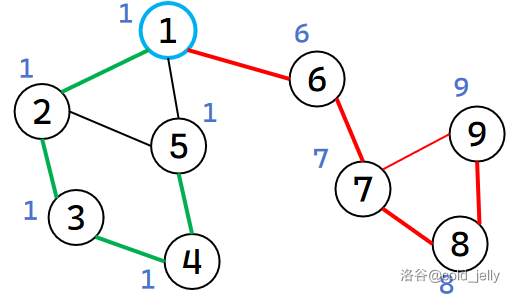
接下来我们遍历到 \(7\) 并发现 \(7\) 已被遍历，所以令 \(low[9]=\min\{low[9],dfn[7]\}=7\)。

\(9\) 没有其它出边了，回溯到 \(8\)，更新 \(low[8]=\min\{low[8],low[9]\}=7\)。

继续回溯到 \(7\)，更新 \(low[7]=\min\{low[7],low[8]\}=7\)，并发现 \(dfn[7]\le low[8]\)。此时我们将 cnt ++（\(cnt=2\)）。我们判定 \(7\) 不是搜索树的根节点，因此认定 \(7\) 为割点并标记。

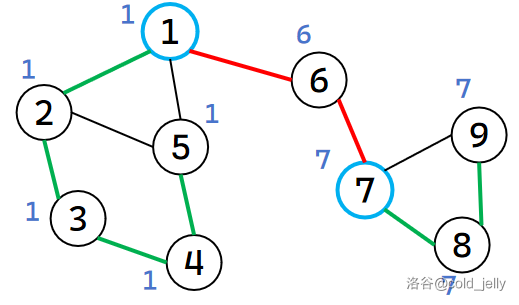
继续回溯到 \(6\)，更新 \(low[6]=\min\{low[6],low[7]\}=6\)，发现 \(dfn[6]<low[7]\)，此时我们将 cnt ++（\(cnt=3\)）。我们判定 \(6\) 不是搜索树的根节点，因此认定 \(6\) 为割点并标记。

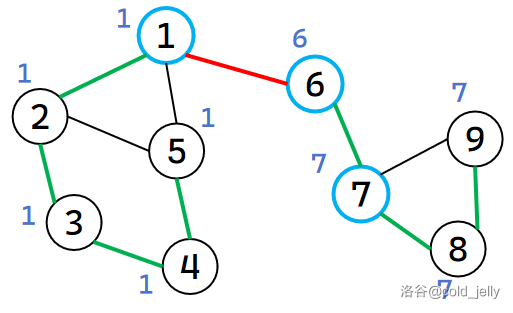
继续回溯到 \(1\)，更新 \(low[1]=\min\{low[1],low[6]\}=1\)，同上标记 \(1\) 为割点（虽然我们之前已经标记过了）。

如果无向图不连通，Tarjan 算法将会在其余连通块上进行类似操作。

Tarjan 算法的代码实现

我们不仅要记录割点，还要记录每个 v-DCC。此时类似于 SCC 和 e-DCC 的记录方法，我们用栈实现。

具体而言，在每次发现 \(dfn[u]\le low[v]\) 时，我们认为有新的 v-DCC，此时我们不断弹栈直到将 \(v\) 弹出，弹出的所有节点属于一个 v-DCC。在最后，我们还应将 \(u\) 也加入 v-DCC。而在 Tarjan 算法每遍历到一个新节点时就将其入栈。

还要注意特判孤立点单独作为一个 v-DCC。

void tarjan(int u)
{
	dfn[u] = low[u] = ++ idx;
	s.push(u);
	if(u == root && h[u] == -1)//孤立点 
	{
		vdcc[++ vDCC].push_back(u);
		return;
	}
	int cnt = 0;
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if(dfn[u] <= low[v])
			{
				cnt ++;
				if(u != root || cnt > 1) cut[u] = true;//记录割点
				vDCC ++;
				int top;
				do
				{
					top = s.top();
					s.pop();
					vdcc[vDCC].push_back(top);
				}while(top != v);
				vdcc[vDCC].push_back(u);
			}
		}
		else low[u] = min(low[u], dfn[v]);
	}
}

模板题 P8435 【模板】点双连通分量 的参考代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 4e6 + 10;
int n, m;
int h[N], e[M], ne[M], ide;
void add(int u, int v)
{
	e[ide] = v, ne[ide] = h[u], h[u] = ide ++;
}
int root;
int dfn[N], low[N], idx;
stack<int> s;
int vDCC;
vector<int> vdcc[N];
bool cut[N];//割点 
void tarjan(int u)
{
	dfn[u] = low[u] = ++ idx;
	s.push(u);
	if(u == root && h[u] == -1)//孤立点 
	{
		vdcc[++ vDCC].push_back(u);
		return;
	}
	int cnt = 0;
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if(dfn[u] <= low[v])
			{
				cnt ++;
				if(u != root || cnt > 1) cut[u] = true;
				vDCC ++;
				int top;
				do
				{
					top = s.top();
					s.pop();
					vdcc[vDCC].push_back(top);
				}while(top != v);
				vdcc[vDCC].push_back(u);
			}
		}
		else low[u] = min(low[u], dfn[v]);
	}
}
int main()
{
	memset(h, -1, sizeof h);
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		if(u == v) continue;
		add(u, v), add(v, u);
	}
	for(int i = 1; i <= n; i ++)
		if(!dfn[i])
		{
			root = i;
			tarjan(i);
		}
	printf("%d\n", vDCC);
	for(int i = 1; i <= vDCC; i ++)
	{
		printf("%d ", vdcc[i].size());
		for(auto j : vdcc[i]) printf("%d ", j);
		puts("");
	}
	return 0;
}

v-DCC 的缩点

我们将每个割点以及每个 v-DCC 均看作一个“大点”，例如若有 \(s_1\) 个割点和 \(s_2\) 个 v-DCC，我们得到的“大点”数为 \(s_1+s_2\)。此时我们建立一张包含所有“大点”的新图，将每个割点与其所属的 v-DCC 对应的“大点”连边，我们可以得到一棵树（或森林）：

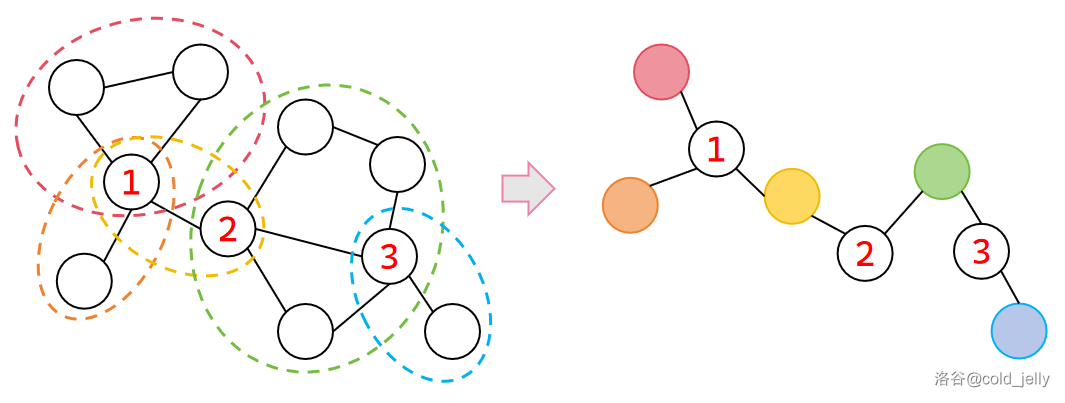
我们扫描每个点，如果是割点，那么我们赋予其一个新的编号，然后扫描 v-DCC，按其颜色继续编号，然后与其包含的割点连边即可。

	idcut = vDCC;//割点对应大点的编号 
	for(int i = 1; i <= n; i ++)
		if(cut[i]) id[i] = ++ idcut;//记录新编号 
	for(int i = 1; i <= vDCC; i ++)
		for(auto j : vdcc[i])
		{
			if(cut[j])//是割点，连边 
			{
				e2[i].push_back(id[j]);
				e2[id[j]].push_back(i);
			}
			else color[j] = i;//非割点，记录颜色 
		}