【图论】总结 6：强连通分量

强连通分量是有向图中的重要概念。

对于有向图 \(G=(V,E)\)，如果 \(\forall u,v\in V\)，既能从 \(u\) 走到 \(v\)，又能从 \(v\) 走到 \(u\)，那么称有向图 \(G\) 是强连通的，而有向图里的极大强连通子图被称为该有向图的一个强连通分量（SCC）。这里的极大是什么意思呢？若图 \(G'\) 是图 \(G\) 的强连通分量，那么是不存在图 \(G''\) 使得 \(G'\subset G''\subset G\) 且 \(G''\) 是图 \(G\) 的强连通分量的。

一个孤立点也是强连通分量。

我们的问题是求一张有向图中的所有强连通分量。

---

有向图的搜索树

对于一张有向图，如果存在一个节点 \(s\)，从 \(s\) 出发能够到达图上任意一点，那么 \(s\) 被称为该有向图的一个源点（类似 SPFA 中提到的超级源点）。一张有向图中可能包含多个源点，我们从中任取一个作为起点，然后进行 DFS，每个点只访问一次，所有遍历到的边及节点构成一棵以源点为根的树，我们称之为该有向图的一棵搜索树。我们在 DFS 时按照每个节点被访问到的顺序给图中每个节点以 \(1\sim n\) 的整数标记，这个整数被称为时间戳，记作 \(dfn[u]\)。

例如下图展示了一张图的搜索树及节点的时间戳（图中加粗绿边为树边，节点内数字为时间戳），我们默认 DFS 时优先遍历更靠左的节点：

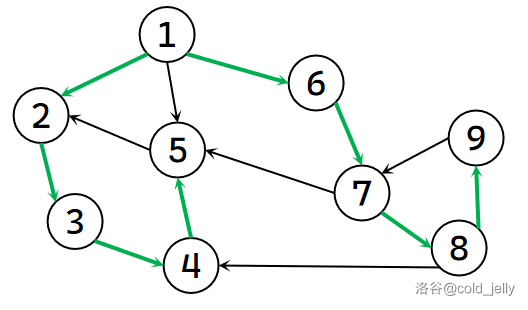
我们可以将有向图中的边 \((u,v)\) 分为 \(4\) 类：

1. 树枝边，即上文所说的“树边”，满足 \(u\) 是 \(v\) 的父节点；
2. 前向边，\(u\) 是 \(v\) 的祖先节点；
3. 后向边，\(v\) 是 \(u\) 的祖先节点；
4. 横叉边，除开上述三种以外的边，其定有 \(dfn[v]<dfn[u]\)，因为如果 \(dfn[v]>dfn[u]\) 直观上表现为在访问到 \(u\) 节点后还可以继续访问未被访问的 \(v\) 节点，那么 \((u,v)\) 应为树枝边才对。

下图展示了上面的例图中边的分类：

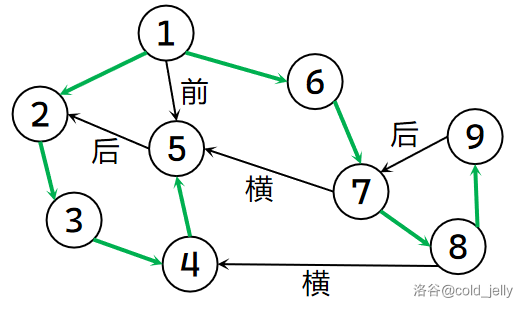
另外，如果一个节点是某个强连通分量在搜索树中遇到的第一个节点，那么该节点被称为该强连通分量的根。

Tarjan 算法

Tarjan 算法能够在线性复杂度内求得有向图的所有强连通分量。

用例子来过一遍 Tarjan 算法的流程，感悟一下。

Tarjan 算法需要用到一个追溯值数组 \(low\)，这个等会会讲到，还需要一个栈 \(s\) 及标记一个节点是否在栈中的标记数组 \(st\)。

在 DFS 过程中，首先进入节点 \(1\)：此时 idx ++（\(idx=1\)），并赋值给 \(dfn[1]\) 以及 \(low[1]\)，将 \(1\) 压入栈并标记；

往下遍历到 \(2\)：此时 idx ++（\(idx=2\)），并赋值给 \(dfn[2]\) 以及 \(low[2]\)，将 \(2\) 压入栈并标记；

以此类推直到遍历到 \(5\)：此时 idx ++（\(idx=5\)），并赋值给 \(dfn[5]\) 以及 \(low[5]\)，将 \(5\) 压入栈并标记；

继续遍历到 \(2\) 号节点，此时发现 \(2\) 被访问过且还在栈中，说明 \(2\) 还在这个强连通分量中（因为会发现这里实际形成了一个 \(2\to 3\to 4\to 5\to 2\) 的环），此时令 \(low[5]=\min\{low[5],dfn[2]\}=2\)。此时场景如下图所示（蓝色数字为目前的追溯值 \(low\)）：

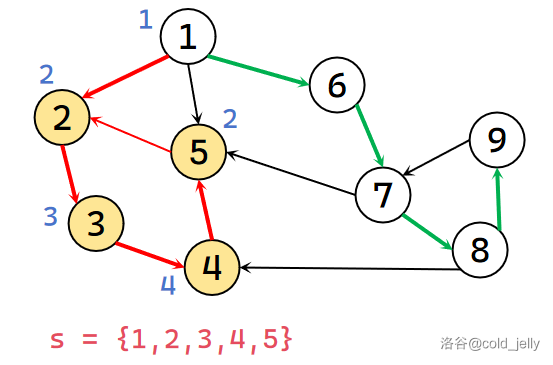
然后 \(5\) 没有出边，所以回溯到 \(4\)，更新 \(low[4]=\min\{low[4],low[5]\}=2\)；

继续回溯到 \(3\)，更新 \(low[3]=\min\{low[3],low[4]\}=2\)；

继续回溯到 \(2\)，更新 \(low[2]=\min\{low[2],low[3]\}=2\)。

然后此时发现 \(low[2]=dfn[2]\) 且 \(2\) 的出边已找完，根据 Tarjan 算法的强连通分量判定法则，\(2\) 即为该强连通分量的根，此时不断弹出栈里元素直到 \(2\) 被弹出，此时被弹出的元素属于同一个 SCC，我们记录下来并标记颜色：

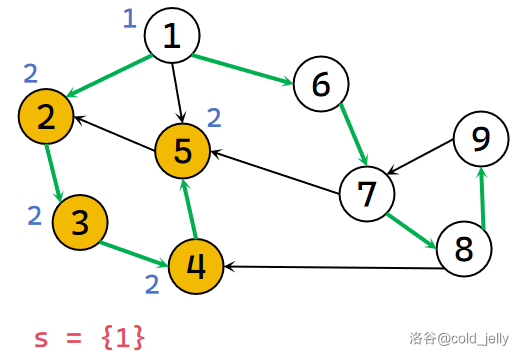
继续回溯到 \(1\)，更新 \(low[1]=\min\{low[1],low[2]\}=1\)。

继续扫描 \(1\) 的出边，遍历到 \(5\)，因为 \(5\) 在之前已经被遍历过了，故 \(idx\) 不变。并且 \(5\) 不在栈中，不用管它：

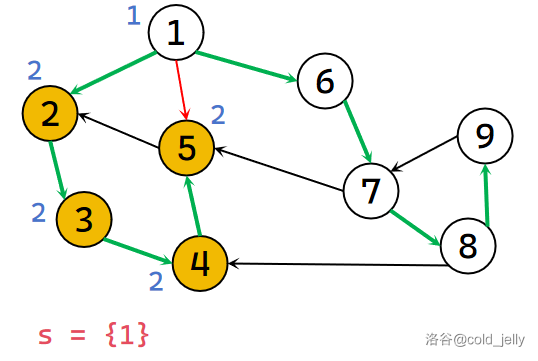
继续扫描 \(1\) 的出边，遍历到 \(6\)：此时 idx ++（\(idx=6\)），并赋值给 \(dfn[6]\) 以及 \(low[6]\)，将 \(6\) 压入栈中并标记；

往下遍历到 \(7\)：此时 idx ++（\(idx=7\)），并赋值给 \(dfn[7]\) 以及 \(low[7]\)，将 \(7\) 压入栈中并标记；

往下遍历到 \(5\)：发现 \(5\) 已经被遍历过了，且 \(5\) 不在栈中，不用管它：

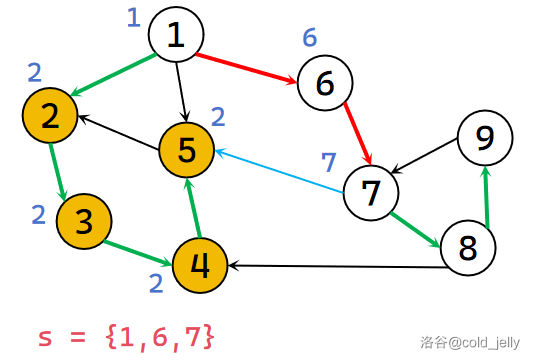
扫描 \(7\) 的出边，遍历到 \(8\)：此时 idx ++（\(idx=8\)），并赋值给 \(dfn[8]\) 以及 \(low[8]\)，将 \(8\) 压入栈中并标记；

往下遍历到 \(4\)：发现 \(4\) 已经被遍历过了，且 \(4\) 不在栈中，不用管它：

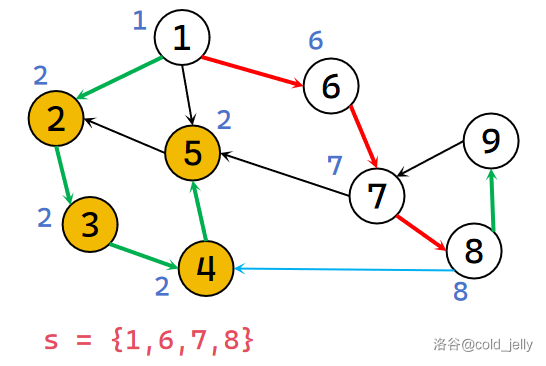
继续扫描 \(8\) 的出边，遍历到 \(9\)：此时 idx ++（\(idx=9\)），并赋值给 \(dfn[9]\) 以及 \(low[9]\)，将 \(9\) 压入栈中并标记；

往下遍历到 \(7\)：\(7\) 被访问过且还在栈中，说明 \(7\) 还在这个强连通分量中（这里有环 \(7\to 8\to 9\to 7\)），此时令 \(low[9]=\min\{low[9],dfn[7]\}=7\)。\(9\) 没有出边，因此回溯更新：\(low[8]=\min\{low[8],low[9]\}=7\)，\(low[7]=\min\{low[7],low[8]\}=7\)。

此时发现 \(low[7]=dfn[7]\) 且 \(7\) 的出边已找完，所以 \(7\) 为该强连通分量的根，不断弹出栈中元素直到 \(7\) 被弹出，此时被弹出的元素同属于一个 SCC，我们记录下来并标记颜色：

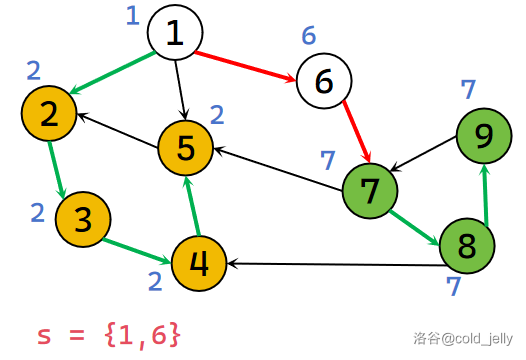
继续回溯到 \(6\)，发现 \(low[6]=dfn[6]\) 且 \(6\) 的出边已找完，所以 \(6\) 为该强连通分量的根，不断弹出栈中元素直到 \(6\) 被弹出，此时被弹出的元素同属于一个 SCC，我们记录下来并标记颜色：

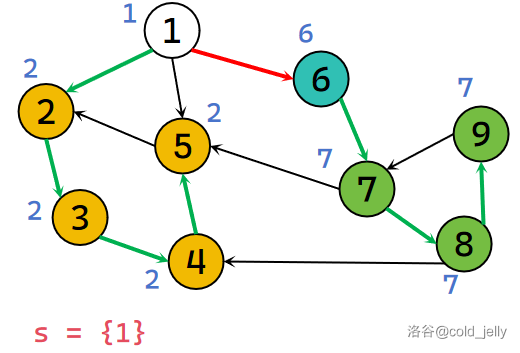
继续回溯到 \(1\)，发现 \(low[1]=dfn[1]\) 且 \(1\) 的出边已找完，所以 \(1\) 为该强连通分量的根，不断弹出栈中元素直到 \(1\) 被弹出，此时被弹出的元素同属于一个 SCC，我们记录下来并标记颜色：

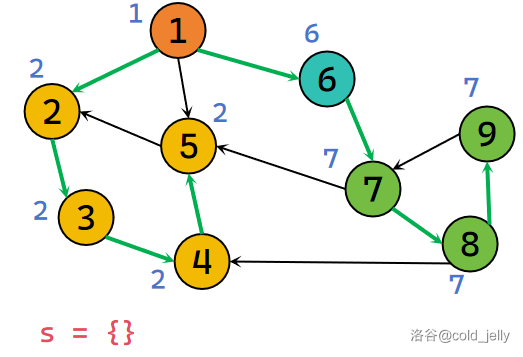
此时栈为空，我们总算处理完了图上的一个连通块。图上还有其它类似的连通块，所以要循环跑多次 Tarjan 算法。

由于我们仅遍历一遍每条边和点 \(1\) 次，所以 Tarjan 算法的时间复杂度为 \(O(n+m)\)。Tarjan 求 SCC 并记录的代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int n, m;
vector<int> e[N];
int dfn[N], low[N], idx;
stack<int> s;
bool st[N];
int SCC;//SCC 个数
vector<int> scc[N];//记录 SCC
void tarjan(int u)
{
	dfn[u] = low[u] = ++ idx;
	s.push(u);
	st[u] = true;
	for(auto v : e[u])
	{
		if(!dfn[v])//v 没有被访问
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);//更新
		}
		else if(st[v]) low[u] = min(low[u], dfn[v]);//更新
	}
	if(low[u] == dfn[u])//发现 SCC
	{
		int top;
		SCC ++;
		do
		{
			top = s.top();
			s.pop();
			st[top] = false;
			scc[SCC].push_back(top);
		}while(top != u);
	}
}
int main()
{
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		e[u].push_back(v);
	}
	for(int i = 1; i <= n; i ++)
		if(!dfn[i]) tarjan(i);//如果节点未被访问，跑 Tarjan
	cout << SCC << "\n";
	for(int i = 1; i <= SCC; i ++)
	{
		for(auto j : scc[i]) printf("%d ", j);
		puts("");
	}
	return 0;
}

通过 Tarjan 算法的实例分析，我们发现追溯值 \(low[u]\) 是满足以下任一条件的所有节点的 \(dfn\) 的最小值：

1. 在 \(\text{SubTree}(u)\)（即搜索树上以 \(u\) 为根的子树）中；
2. \(\text{SubTree}(u)\) 上通过一条非树枝边能到达的且在栈中的节点。

SCC 的缩点

我们像下图一样把有向图上每个 SCC 看作一个“大点”，从而得到一个 DAG 的过程就叫做缩点。

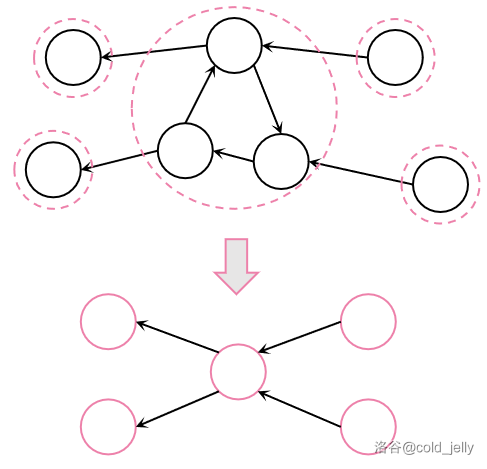
因为缩点后的 DAG 可以进行拓扑排序，有助于我们做图上处理，所以其是一种常用的解题手段。

怎么缩点呢？我们在 Tarjan 算法求 SCC 的过程中可以记录一个颜色数组 \(color[i]\) 表示 \(i\) 号节点属于哪个 SCC，并在输入时记录有向边的起点 \(u[N]\) 和终点 \(v[N]\)。在缩点时扫描每条边，如果当前边的起终点不在同一个 SCC 中，那么以 SCC 的颜色为编号，连有向边 \((color[u[i]],color[v[i]])\) 即可。

for(int i = 1; i <= m; i ++)
	if(color[u[i]] != color[v[i]])
		e2[color[u[i]]].push_back(color[v[i]]);