Luogu P9260 [PA 2022] Miny 题解

题目描述

有一颗 \(n\) 个节点的树，树上的每一个点有一个爆炸半径 \(r_i\)，每条边 \((a_i,b_i)\) 有一个长度 \(c_i\)，一个炸弹 \(i\) 能引爆另一个炸弹 \(j\) 当且仅当 \(dis(i,j)\le r_i\)。

问题分析

我们可以建一个有向图 \(G\)，对于 \(\forall i,j\ dis(i,j)\le r_i\) 建一条有向边 \(i\to j\)，但显然我们不可能接受这种数量级达到 \(n^2\) 的建边方法，我们不妨进行点分治优化建图，对于每次子树的重心 \(i\) ,求子树中每个点 \(j\) 到 \(i\) 的距离 \(dis_j\)，并按 \(dis_j\) 从小到大排序 \(j\) 得到序列 \(a\)，那么 \(dis(i,j)\le r_i\) 改写成 \(dis_i+dis_j\le r_i\)，即 \(dis_j\le r_u-dis_i\)，我们不难发现点 \(i\) 可以连的点 \(j\) 是序列 \(a\) 的前缀。所以我们又可以前缀优化建图，二分找到前缀的结束位置 \(k\)，将 \(i\) 连接到对应区间 \(a_1\) 到 \(a_k\) 的虚点上，然后将所有建出来的虚点相邻连接，并且将相邻虚点 \(i\) 与 \(j\) 之间的实点部分与 \(j\) 相连。具体化地可以见下图：

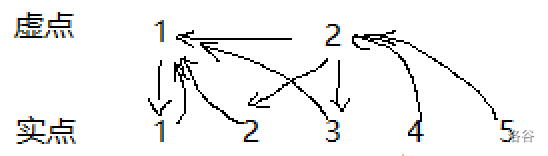
（这张图代表的是实点 \(1\) 到 \(3\) 的前缀区间为 \([1,1]\)，实点 \(4\) 到 \(5\) 的前缀区间为 \([1,3]\) 时的连边情况，其中虚点 \(1\) 代表实点区间 \([1,1]\)，虚点 \(2\) 代表实点区间 \([1,3]\)）

通过前缀和与点分治优化建图我们可以将 \(n^2\) 条边优化到 \(n\log n\) 条边。
接下来我们便可以对有向图 \(G\) 进行缩点，对于每个 SCC 内的点，他们之间是可以互相引爆的，于是我们只需判断 SCC 之间的可达性便可以了，显然我们使用 bitset，但如果对于每个 SCC 开一个 bitset，那么空间上必然不优，将达到 \(O(\frac{n^2\log n}{w})\)，所以我们对 SCC 进行分块，每次仅处理 \(bl\) 个 SCC 之间的可达性，空间复杂度降至 \(O(\frac{n\cdot bl\log n}{w})\)，时间复杂度依然为 \(O(n\log^2n+\frac{n^2\log n}{\omega})\)，经实测检验当 \(bl=2000\) 很优。

CODE

#include<bits/stdc++.h>
using namespace std;
namespace fastio{
	#define il inline
	const int isz=1<<25;
	char iin[isz],*is=iin+isz,*it=iin+isz;
	#define gc() (is==it)?(it=(is=iin)+fread(iin,1,isz,stdin),(is==it)?EOF:*is++):*is++
	template<typename T> il void rd(T &x){
		x=0;
		char c=gc();
		bool fla=false;
		while(!isdigit(c)) fla|=(c=='-'),c=gc();
		while(isdigit(c)) x=(x<<1)+(x<<3)+(c&15),c=gc();
		x=(fla)?-x:x;
	}
	template<typename T1,typename...T2> il void rd(T1 &x,T2&...y){rd(x);rd(y...);}
	template<typename T> il void rd(T a[],T s,T t){for(T i=s;i<=t;i++) rd(a[i]);}
	char iout[isz],*ita=iout;
	#define Flush() fwrite(iout,1,ita-iout,stdout);ita=iout
	template<typename T> il void wr(T x,char la='\n'){
		char c[35];
		int len=0;
		if(x<0) *ita++='-',x=-x;
		do{c[++len]=(x%10+'0');x/=10;}while(x);
		while(len)*ita++=c[len--];
		*ita++=la;
	} 
	il void en(char x){*ita++=x;}
}
using namespace fastio;
const int N=1e5+5,bl=2000;
#define int long long
int n,r[N],sz[N],del[N],dis[N],vir[N],tot,dfn[20*N],low[20*N],in[20*N],idx,id[20*N],scc,num,ans[N];
vector<int> e[N],w[N],g[20*N];
vector<pair<int,int> > line;
stack<int> q;
pair<int,int> s[400*N];
bitset<bl+10> f[20*N];
int rt_check(int x,int fa,int y,int &rt){
    sz[x]=1;
    int maxx=0;
    for(auto i:e[x])if(i!=fa&&!del[i]){rt_check(i,x,y,rt);sz[x]+=sz[i];maxx=max(maxx,sz[i]);}
    maxx=max(maxx,y-sz[x]);
    if((maxx<<1)<=y) rt=x;
    return sz[x];
}
void cal(int x,int fa){
    sz[x]=1;
    line.push_back({dis[x],x});
    for(int i=0;i<e[x].size();i++) if(e[x][i]!=fa&&!del[e[x][i]]){dis[e[x][i]]=dis[x]+w[x][i];cal(e[x][i],x);sz[x]+=sz[e[x][i]];}
}
void dfs(int x,int sz){
    if(sz==1) return;
    int rt;
    rt_check(x,x,sz,rt);
    del[rt]=1;
    dis[rt]=0;
    line.clear();
    cal(rt,rt);
    sort(line.begin(),line.end());
    memset(vir,0,sizeof vir);
    for(auto i:line){
        int ttt=upper_bound(line.begin(),line.end(),make_pair(r[i.second]-dis[i.second],n+1))-line.begin();
        ttt--;
        if(ttt>=0){if(!vir[ttt]){vir[ttt]=++tot;g[tot].push_back(line[ttt].second);}g[i.second].push_back(vir[ttt]);}
    }
    int la=-1;
    for(int i=line.size()-1;i>=0;i--) 
        if(vir[i]){
            if(la!=-1){
                g[vir[la]].push_back(vir[i]);
                for(int j=i+1;j<la;j++) g[vir[la]].push_back(line[j].second);
            }
            la=i;
        }
    if(la!=-1)for(int j=0;j<la;j++)g[vir[la]].push_back(line[j].second);
    for(auto i:e[rt]) if(!del[i]) dfs(i,::sz[i]);
}
void tarjan(int x){
    dfn[x]=low[x]=++idx;
    in[x]=1;
    q.push(x);
    for(auto i:g[x]){if(!dfn[i]){tarjan(i);low[x]=min(low[x],low[i]);}else if(in[i])low[x]=min(low[x],dfn[i]);}
    if(low[x]==dfn[x]){++scc;int ttt;do{ttt=q.top();q.pop();in[ttt]=0;id[ttt]=scc;}while(ttt!=x);}
}
signed main(){
    rd(n);
    rd(r,1ll*1,n);
    for(int i=1;i<n;i++){int x,y,z;rd(x,y,z);e[x].push_back(y);e[y].push_back(x);w[x].push_back(z);w[y].push_back(z);}
    tot=n;
    dfs(1,n);
    for(int i=1;i<=tot;i++) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=tot;i++) for(auto j:g[i]) if(id[i]!=id[j]) s[num++]={id[j],id[i]};
    int maxn=0;
    for(int i=1;i<=n;i++) maxn=max(maxn,id[i]);
    sort(s,s+num);
    num=unique(s,s+num)-s;
    auto solve=[maxn](int l,int r){
        for(int i=1;i<=maxn;i++) f[i].reset();
        for(int i=l;i<=r;i++) f[id[i]].set(i-l);
        for(int i=0;i<num;i++) f[s[i].second]|=f[s[i].first];
        for(int i=1;i<=n;i++) ans[i]+=f[id[i]].count();
    };
    for(int i=1;i<=n;i+=bl) solve(i,min(i+bl-1,n));
    for(int i=1;i<=n;i++) wr(ans[i],' ');
    Flush();
    return 0;
}