由于水平原因，博客大部分内容摘抄于网络，如有错误或者侵权请指出，本人将尽快修改

反向传播

🔍 神经网络结构与前向传播解析

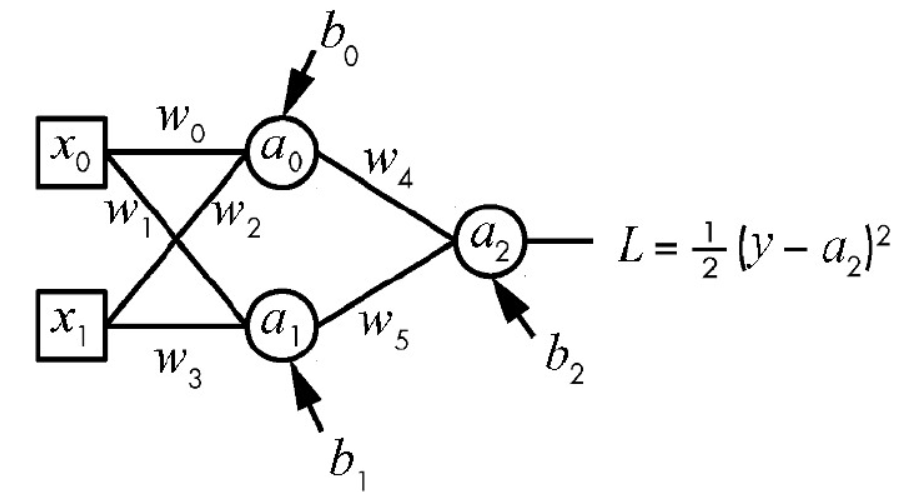
这是一个典型的两层全连接神经网络（1个隐藏层 + 1个输出层），我帮你拆解一下它的结构和前向传播过程：
image

🔎 网络结构

  • 输入层：2个神经元，输入为 \(x_0, x_1\)
  • 隐藏层：2个神经元，激活函数为S型函数（sigmoid）
  • 输出层：1个神经元，无激活函数（线性输出）
  • 可学习参数：6个权重 \(w_0 \sim w_5\) 和3个偏置 \(b_0 \sim b_2\)

🔄 前向传播计算步骤

1. 隐藏层计算

对于隐藏层的每个神经元，先计算加权输入和，再通过sigmoid激活函数得到输出：

\[\begin{align*} z_0 &= w_0 x_0 + w_2 x_1 + b_0 \\ a_0 &= \sigma(z_0) = \frac{1}{1 + e^{-z_0}} \\ z_1 &= w_1 x_0 + w_3 x_1 + b_1 \\ a_1 &= \sigma(z_1) = \frac{1}{1 + e^{-z_1}} \end{align*} \]

2. 输出层计算

输出层直接对隐藏层的输出进行加权求和，不使用激活函数：

\[a_2 = w_4 a_0 + w_5 a_1 + b_2 \]

3. 损失函数定义

平方误差损失函数为：

\[L = \frac{1}{2} \left( y - a_2 \right)^2 \]

其中 \(y\) 是样本标签（0或1）,可以看作常量。\(a_2\) 是网络的预测输出。

损失函数与梯度计算

在损失函数 $ L $ 的输入中，真实标签 $ y $ 为常量，网络输出 $ a_2 $ 为直接自变量。然而，由于 $ a_2 $ 是神经网络前向传播的结果，其值依赖于模型参数：

\[a_2 = f(w_4, w_5, b_2, a_0, a_1) \]

而中间激活值 $ a_0 $ 和 $ a_1 $ 又由输入 $ x_0, x_1 $ 和底层参数决定：

\[a_0 = g_0(w_0, w_1, b_0, x_0, x_1), \quad a_1 = g_1(w_2, w_3, b_1, x_0, x_1) \]

因此，$ a_2 $ 实质上是所有权重和偏置的复合函数。由此，损失函数可表示为关于模型参数 $ \theta $ 的函数：

\[L(\theta; x, y) \]

其中：

  • $ \theta = { w_0, w_1, w_2, w_3, w_4, w_5, b_0, b_1, b_2 } $ 为所有可学习参数（权重与偏置）的集合，作为自变量；
  • $ x = (x_0, x_1) $ 为输入特征；
  • $ y $ 为真实标签；
  • $ x_0, x_1, y $ 在当前计算中视为常量。

梯度计算

为了优化模型参数，我们需要计算损失函数对每个参数的偏导数，即梯度向量 $ \nabla_\theta L(\theta; x, y) $。

具体地，需计算以下 9 个偏导数：

\[\begin{aligned} &\frac{\partial L}{\partial w_0},\ \frac{\partial L}{\partial w_1},\ \frac{\partial L}{\partial w_2},\ \frac{\partial L}{\partial w_3},\ \frac{\partial L}{\partial w_4}, \\ &\frac{\partial L}{\partial w_5},\ \frac{\partial L}{\partial b_0},\ \frac{\partial L}{\partial b_1},\ \frac{\partial L}{\partial b_2} \end{aligned} \]

这些偏导数通过链式法则（Backpropagation）逐层反向传播计算，构成梯度下降等优化算法的基础

🧮 误差反向传播（BP）梯度推导

核心前提：
损失函数为 $ L = \frac{1}{2}(y - a_2)^2 $，则

\[\frac{\partial L}{\partial a_2} = a_2 - y \]

一、正向传播公式回顾（变量依赖关系）

给定输入 $ x_0, x_1 $，参数 $ w_0 \sim w_5, b_0, b_1, b_2 $，前向计算如下：

\[\begin{aligned} z_0 &= w_0 x_0 + w_2 x_1 + b_0, & a_0 &= \sigma(z_0) \\ z_1 &= w_1 x_0 + w_3 x_1 + b_1, & a_1 &= \sigma(z_1) \\ a_2 &= w_4 a_0 + w_5 a_1 + b_2 \end{aligned} \]

其中 \(\sigma(z)\) 是 sigmoid 激活函数，其导数满足：

\[\sigma'(z) = \sigma(z)(1 - \sigma(z)) \]

二、反向传播：逐层计算偏导数

我们需计算损失 \(L\) 对全部 9 个参数 的偏导数。按从输出到输入的顺序进行。

第1组：输出层参数（直接连接 \(a_2\)）

由于 \(a_2 = w_4 a_0 + w_5 a_1 + b_2\)，对这些参数求导非常直接：

\[\begin{aligned} \frac{\partial L}{\partial w_4} &= \frac{\partial L}{\partial a_2} \cdot \frac{\partial a_2}{\partial w_4} = (a_2 - y) \cdot a_0 \\ \frac{\partial L}{\partial w_5} &= \frac{\partial L}{\partial a_2} \cdot \frac{\partial a_2}{\partial w_5} = (a_2 - y) \cdot a_1 \\ \frac{\partial L}{\partial b_2} &= \frac{\partial L}{\partial a_2} \cdot \frac{\partial a_2}{\partial b_2} = (a_2 - y) \cdot 1 = a_2 - y \end{aligned} \tag{输出层} \]

第2组：隐藏层第1个神经元（对应 \(z_1, a_1\)）

该路径为：
$ L \to a_2 \to a_1 \to z_1 \to (w_1, w_3, b_1) $

先计算误差信号在 \(z_1\) 处的值（即 \(\delta_1 = \frac{\partial L}{\partial z_1}\)）：

\[\delta_1 = \frac{\partial L}{\partial z_1} = \underbrace{\frac{\partial L}{\partial a_2}}_{a_2 - y} \cdot \underbrace{\frac{\partial a_2}{\partial a_1}}_{w_5} \cdot \underbrace{\frac{\partial a_1}{\partial z_1}}_{a_1(1 - a_1)} = (a_2 - y) \cdot w_5 \cdot a_1(1 - a_1) \]

然后分别对参数求导（注意 \(z_1 = w_1 x_0 + w_3 x_1 + b_1\)）：

\[\begin{aligned} \frac{\partial L}{\partial b_1} &= \delta_1 \cdot \frac{\partial z_1}{\partial b_1} = \delta_1 \cdot 1 = (a_2 - y) w_5 a_1(1 - a_1) \\ \frac{\partial L}{\partial w_1} &= \delta_1 \cdot \frac{\partial z_1}{\partial w_1} = \delta_1 \cdot x_0 = (a_2 - y) w_5 a_1(1 - a_1) x_0 \\ \frac{\partial L}{\partial w_3} &= \delta_1 \cdot \frac{\partial z_1}{\partial w_3} = \delta_1 \cdot x_1 = (a_2 - y) w_5 a_1(1 - a_1) x_1 \end{aligned} \tag{隐藏层-1} \]

第3组：隐藏层第0个神经元（对应 \(z_0, a_0\)）

该路径为：
$ L \to a_2 \to a_0 \to z_0 \to (w_0, w_2, b_0) $

同理，先算误差信号 \(\delta_0 = \frac{\partial L}{\partial z_0}\)：

\[ \delta_0 = \frac{\partial L}{\partial z_0} = \underbrace{\frac{\partial L}{\partial a_2}}_{a_2 - y} \cdot \underbrace{\frac{\partial a_2}{\partial a_0}}_{w_4} \cdot \underbrace{\frac{\partial a_0}{\partial z_0}}_{a_0(1 - a_0)} = (a_2 - y) \cdot w_4 \cdot a_0(1 - a_0) \]

再对参数求导（\(z_0 = w_0 x_0 + w_2 x_1 + b_0\)）：

\[\begin{aligned} \frac{\partial L}{\partial b_0} &= \delta_0 = (a_2 - y) w_4 a_0(1 - a_0) \\ \frac{\partial L}{\partial w_0} &= \delta_0 \cdot x_0 = (a_2 - y) w_4 a_0(1 - a_0) x_0 \\ \frac{\partial L}{\partial w_2} &= \delta_0 \cdot x_1 = (a_2 - y) w_4 a_0(1 - a_0) x_1 \end{aligned} \tag{隐藏层-0} \]

三、最终结果汇总表（9个偏导数）

参数 偏导数表达式
\(\dfrac{\partial L}{\partial w_4}\) \((a_2 - y) \cdot a_0\)
\(\dfrac{\partial L}{\partial w_5}\) \((a_2 - y) \cdot a_1\)
\(\dfrac{\partial L}{\partial b_2}\) \(a_2 - y\)
\(\dfrac{\partial L}{\partial b_1}\) \((a_2 - y) \cdot w_5 \cdot a_1(1 - a_1)\)
\(\dfrac{\partial L}{\partial w_1}\) \((a_2 - y) \cdot w_5 \cdot a_1(1 - a_1) \cdot x_0\)
\(\dfrac{\partial L}{\partial w_3}\) \((a_2 - y) \cdot w_5 \cdot a_1(1 - a_1) \cdot x_1\)
\(\dfrac{\partial L}{\partial b_0}\) \((a_2 - y) \cdot w_4 \cdot a_0(1 - a_0)\)
\(\dfrac{\partial L}{\partial w_0}\) \((a_2 - y) \cdot w_4 \cdot a_0(1 - a_0) \cdot x_0\)
\(\dfrac{\partial L}{\partial w_2}\) \((a_2 - y) \cdot w_4 \cdot a_0(1 - a_0) \cdot x_1\)

四、使用说明

在训练时，对每个样本 \((x_0, x_1, y)\)：

  1. 前向传播：计算 \(a_0, a_1, a_2\)
  2. 反向传播：代入上表公式，计算9个偏导数
  3. 参数更新（例如用学习率 \(\eta\)）：

    \[w_i \leftarrow w_i - \eta \cdot \frac{\partial L}{\partial w_i}, \quad b_j \leftarrow b_j - \eta \cdot \frac{\partial L}{\partial b_j} \]

这样就完成了单样本的反向传播全过程。

🧠 神经网络训练的梯度下降详解

我们训练一个三层全连接网络：

  • 输入：$ x = (x_0, x_1) $
  • 隐藏层：2 个 sigmoid 神经元 → 输出 $ a_0, a_1 $
  • 输出层：线性组合 → $ a_2 $（可视为 logits，或直接用于 MSE）
  • 损失函数：$ L = \frac{1}{2}(y - a_2)^2 $
  • 可学习参数共 9 个：

    \[\theta = (w_0, w_1, w_2, w_3, w_4, w_5, b_0, b_1, b_2) \]

步骤 1：定义目标函数与梯度

  • 目标函数（损失）：

    \[L(\theta; x, y) = \frac{1}{2}(y - a_2(\theta))^2 \]

    其中 $ a_2(\theta) $ 是通过前向传播由 \(\theta\) 和输入 \(x\) 决定的。

  • 梯度向量（9 维）：

    \[\nabla_\theta L = \left( \frac{\partial L}{\partial w_0}, \frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \frac{\partial L}{\partial w_3}, \frac{\partial L}{\partial w_4}, \frac{\partial L}{\partial w_5}, \frac{\partial L}{\partial b_0}, \frac{\partial L}{\partial b_1}, \frac{\partial L}{\partial b_2} \right)^T \]

    各分量按上一节表格计算。

步骤 2：初始化参数

  • 随机初始化所有权重和偏置（例如用小随机数）：

    \[\begin{aligned} &w_0^{(0)} = 0.1,\ w_1^{(0)} = -0.2,\ w_2^{(0)} = 0.3,\ w_3^{(0)} = 0.15,\\ &w_4^{(0)} = -0.1,\ w_5^{(0)} = 0.2,\\ &b_0^{(0)} = 0.0,\ b_1^{(0)} = 0.0,\ b_2^{(0)} = 0.0 \end{aligned} \]

    记为初始参数向量 $ \theta^{(0)} $。

  • 设置超参数：

    • 学习率：$ \eta = 0.1 $
    • 收敛阈值：$ \varepsilon = 10^{-5} $
    • 最大迭代次数：$ N_{\text{max}} = 1000 $

步骤 3：对单个样本进行一次训练迭代（类比你的 k=0,1,...）

假设当前样本为：

\[x_0 = 5.1,\quad x_1 = 3.5,\quad y = 1 \quad \text{（例如“setosa”类标签为1）} \]

▶ 第 0 轮（k = 0）

  1. 前向传播（用 $ \theta^{(0)} $）：

    • $ z_0 = w_0 x_0 + w_2 x_1 + b_0 = 0.1 \times 5.1 + 0.3 \times 3.5 + 0 = 1.56 $
    • $ a_0 = \sigma(1.56) \approx 0.826 $
    • $ z_1 = w_1 x_0 + w_3 x_1 + b_1 = (-0.2)\times5.1 + 0.15\times3.5 \approx -0.495 $
    • $ a_1 = \sigma(-0.495) \approx 0.379 $
    • $ a_2 = w_4 a_0 + w_5 a_1 + b_2 = (-0.1)(0.826) + 0.2(0.379) \approx 0.0068 $

  2. 计算损失：

    \[L = \frac{1}{2}(1 - 0.0068)^2 \approx 0.493 \]

  3. 反向传播：计算梯度（代入公式）

    • $ \delta = a_2 - y = 0.0068 - 1 = -0.9932 $
    • 输出层：
      • $ \frac{\partial L}{\partial w_4} = \delta \cdot a_0 \approx -0.9932 \times 0.826 \approx -0.820 $
      • $ \frac{\partial L}{\partial w_5} = \delta \cdot a_1 \approx -0.9932 \times 0.379 \approx -0.376 $
      • $ \frac{\partial L}{\partial b_2} = \delta \approx -0.9932 $
    • 隐藏层（第1个神经元）：
      • $ \delta_1 = \delta \cdot w_5 \cdot a_1(1 - a_1) \approx (-0.9932)(0.2)(0.379)(1 - 0.379) \approx -0.047 $
      • $ \frac{\partial L}{\partial w_1} = \delta_1 \cdot x_0 \approx -0.047 \times 5.1 \approx -0.240 $
      • $ \frac{\partial L}{\partial w_3} = \delta_1 \cdot x_1 \approx -0.047 \times 3.5 \approx -0.165 $
      • $ \frac{\partial L}{\partial b_1} = \delta_1 \approx -0.047 $
    • 隐藏层（第0个神经元）：
      • $ \delta_0 = \delta \cdot w_4 \cdot a_0(1 - a_0) \approx (-0.9932)(-0.1)(0.826)(0.174) \approx +0.0142 $
      • $ \frac{\partial L}{\partial w_0} = \delta_0 \cdot x_0 \approx 0.0142 \times 5.1 \approx 0.072 $
      • $ \frac{\partial L}{\partial w_2} = \delta_0 \cdot x_1 \approx 0.0142 \times 3.5 \approx 0.050 $
      • $ \frac{\partial L}{\partial b_0} = \delta_0 \approx 0.0142 $

  4. 计算梯度范数（判断是否收敛）：

    \[\|\nabla_\theta L\| = \sqrt{(-0.820)^2 + (-0.376)^2 + \cdots + (0.072)^2} \approx 1.02 > \varepsilon \]

  5. 参数更新（梯度下降）：

    \[\theta^{(1)} = \theta^{(0)} - \eta \cdot \nabla_\theta L \]

    例如：

    • $ w_4^{(1)} = w_4^{(0)} - 0.1 \times (-0.820) = -0.1 + 0.082 = -0.018 $
    • $ w_0^{(1)} = 0.1 - 0.1 \times 0.072 = 0.0928 $
    • $ b_2^{(1)} = 0 - 0.1 \times (-0.9932) = 0.0993 $
    • ……（其余类似）

🔁 这一步完全对应你例子中的：
$ x_1 = x_0 - \alpha \cdot f_x' $，只是现在有 9 个变量同时更新。

步骤 4：重复迭代直到收敛

  • 对同一个样本继续迭代（在线学习），或遍历整个数据集（批量/随机梯度下降）。
  • 每轮计算新的 $ a_2 $、损失 \(L\)、梯度 \(\nabla_\theta L\)。
  • 当 $ |\nabla_\theta L| < \varepsilon $ 或达到最大轮数时停止。

步骤 5：最终结果

  • 得到最优参数 $ \theta^* \approx (w_0^, \dots, b_2^) $
  • 此时模型对训练样本的预测误差最小：$ a_2 \approx y $
  • 损失 $ L \to 0 $（理想情况下）

✅ 总结：神经网络训练 = 高维梯度下降

最终公式（通用形式）

对任意参数 \(\theta_i\)，更新规则为：

\[\boxed{ \theta_i^{(k+1)} = \theta_i^{(k)} - \eta \cdot \frac{\partial L}{\partial \theta_i} \Bigg|_{\theta = \theta^{(k)}} } \]

这正是你最初写的 $ x_{k+1} = x_k - \alpha f'(x_k) $ 在高维、复合函数下的推广。

posted @ 2026-02-02 22:20  小纸条  阅读(4)  评论(0)    收藏  举报