207. 课程表

207. 课程表

题目描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。

• 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

 

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

 

提示：

• 1 <= numCourses <= 105
• 0 <= prerequisites.length <= 5000
• prerequisites[i].length == 2
• 0 <= ai, bi < numCourses
• prerequisites[i] 中的所有课程对 互不相同

解法

Java

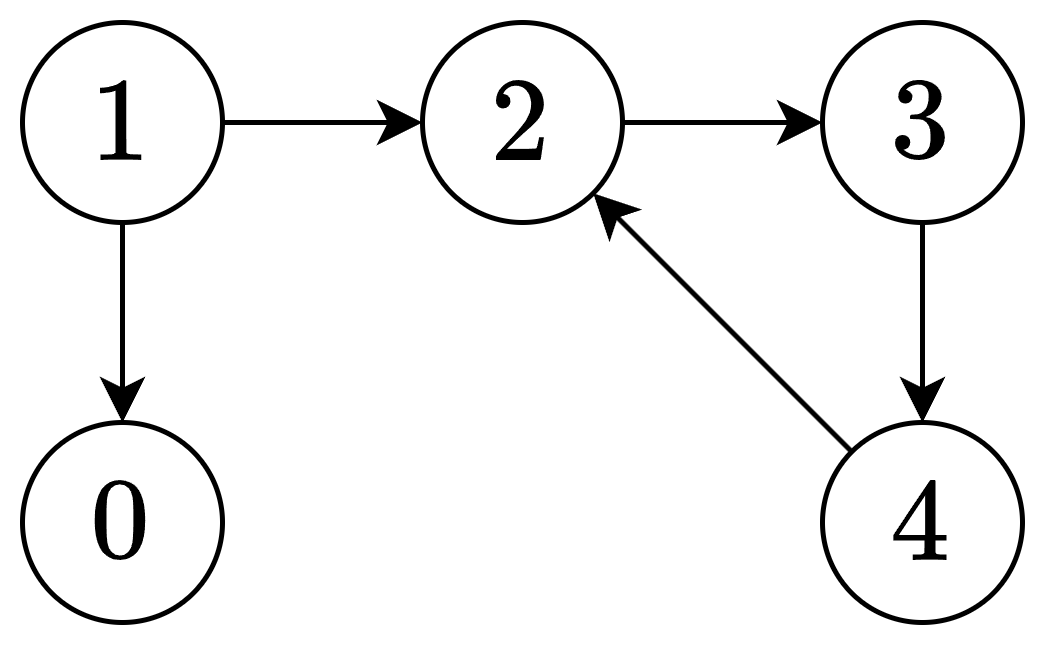
例如 1→2→3→4→2，走到 4 的时候，发现下一个节点 2 在递归栈中（正在访问中），那么就找到了环。

注：我们说节点 x「正在访问中」，是说我们正在递归处理节点 x 以及它的后续节点，dfs(x) 尚未结束。

具体思路
对于每个节点 x，都定义三种颜色值（状态值）：

0：节点 x 尚未被访问到。

1：节点 x 正在访问中，dfs(x) 尚未结束。

2：节点 x 已经完全访问完毕。注意这还说明从 x 出发无法找到环。所以当我们遇到状态值为 2 的节点 x 时，无需递归 x。

⚠误区：不能只用两种状态表示节点「没有访问过」和「访问过」。例如上图，我们先 dfs(0)，再 dfs(1)，此时 1 的邻居 0 已经访问过，但这并不能表示此时就找到了环。

public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 构建邻接表（列表数组）
        List<Integer>[] adj = new List[numCourses];
        for (int i = 0; i < numCourses; i++) {
            adj[i] = new ArrayList<>();
        }
        for (int[] pre : prerequisites) {
            int prerequisite = pre[1];
            int course = pre[0];
            adj[prerequisite].add(course); // 先修课 -> 后续课
        }

        // 两种状态：0=未访问，1=当前路径中正在访问（临时标记），2=已经访问过。不能使用boolean[] 是否访问过
        int[] visited = new int[numCourses];

        // 遍历每个未访问的节点
        for (int i = 0; i < numCourses; i++) {
            if (visited[i] == 0 && hasCycle(i, adj, visited)) {
                return false; // 有环，无法完成
            }
        }
        return true;
    }

    private boolean hasCycle(int curr, List<Integer>[] adj, int[] visited) {
        // 若当前节点在“当前路径中已访问”，说明有环
        if (visited[curr] == 1) {
            return true;
        }
        if (visited[curr] == 2) {
            return false;
        }
        // 标记为“当前路径中正在访问”
        visited[curr] = 1;

        // 遍历所有后续课程
        for (int next : adj[curr]) {
            if (hasCycle(next, adj, visited)) {
                return true; // 子节点有环
            }
        }
        // 回溯：退出当前路径
        visited[curr] = 2;
        return false;
    }

使用两种状态，会超时

import java.util.*;

public class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 构建邻接表（列表数组）
        List<Integer>[] adj = new List[numCourses];
        for (int i = 0; i < numCourses; i++) {
            adj[i] = new ArrayList<>();
        }
        for (int[] pre : prerequisites) {
            int course = pre[0];
            int prerequisite = pre[1];
            adj[prerequisite].add(course); // 先修课 -> 后续课
        }

        // 两种状态：0=未访问，1=当前路径中正在访问（临时标记）
        int[] visited = new int[numCourses];

        // 遍历每个未访问的节点
        for (int i = 0; i < numCourses; i++) {
            if (hasCycle(i, adj, visited)) {
                return false; // 有环，无法完成
            }
        }
        return true;
    }

    private boolean hasCycle(int curr, List<Integer>[] adj, int[] visited) {
        // 若当前节点在“当前路径中已访问”，说明有环
        if (visited[curr] == 1) {
            return true;
        }
        // 标记为“当前路径中正在访问”
        visited[curr] = 1;

        // 遍历所有后续课程
        for (int next : adj[curr]) {
            if (hasCycle(next, adj, visited)) {
                return true; // 子节点有环
            }
        }

        // 回溯：退出当前路径，清除标记（允许其他路径访问）
        visited[curr] = 0;
        return false;
    }

    
}

...