深度优先搜索

深度优先搜索( DFS, Depth-First Search) 是搜索的手段之一。它从某个状态开始，不断地转移状态直到无法转移,然后回退到前一步的状态 ,继续转移到其他状态，如此不断重复，直至找到最终的解。例如求解数独，首先在某个格子内填人适当的数字，然后再继续在下一个格子内填入数字，如此继续下去。如果发现某个格子无解了，就放弃前一个格 子上选择的数字，改用其他可行的数字。根据深度优先搜索的特点，采用递归函数实现比较简单。

上诉状态转移顺序和二叉树的前序遍历一致，二叉树的前序遍历就是dfs。上面这颗二叉树的前序遍历是：12345678910

---

 

题目：

给定n个整数a1、a2、.......an，判断是否可以从中选出若干数，使它们的和恰好为K。

输入：

n=4

a={1,2,4,7}

k=13

输出：

Yes（13=2+4+7）

从a开始按顺序决定每个数加或不加，在全部n个数都决定后再判断它们的和是不是k即可。因为状态数是2"+1（每个数有两种取法，所有数都不取和空集，虽然二者在效果上都是0，但是属于两种状态）,所以复杂度是0(2")。如何实现这个搜索，请参见下面的代码。注意a的下标与题目描述中的下标偏移了1。在程序中使用的是0起始的下标规则，题目描述中则是1开始的，这一点要注意避免搞混。 

深度优先搜索从最开始的状态出发,遍历所有可以到达的状态。由此可以对所有的状态进行操作,或者列举出所有的状态。 

---

 

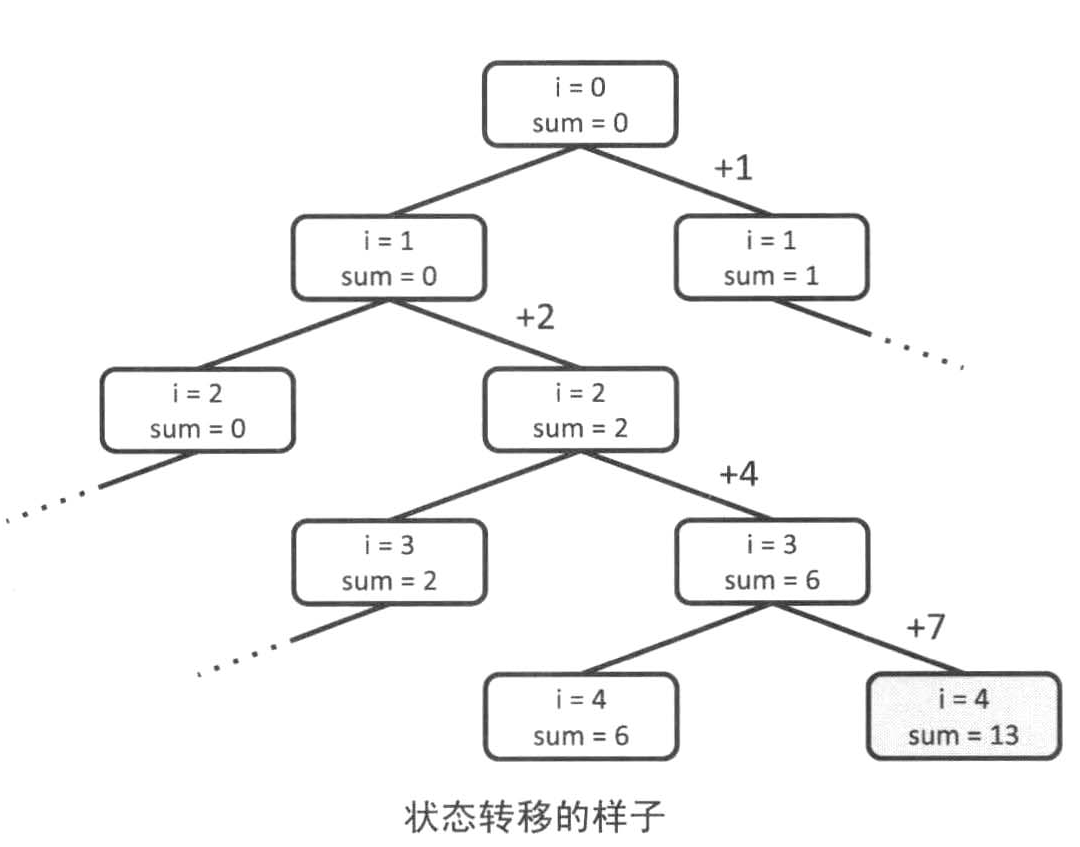
上述转移状态中二叉树的每一层都是相同的数字，第一层是a[1]，第二层是a[2]，第三层是a[3]......

java版本解法：

package dfs;

public class Main {
	static int []a;
	static int n,k;//一共n个数;若干个数和为k
	static boolean dfs(int i,int sum){
		if (i==n) {
			return k==sum;
		}
		boolean x=dfs(i+1,sum+a[i]);
		boolean y= dfs(i+1,sum);
		return x||y;
	}
	public static void main(String[] args) {
		n=4;
		a=new int[]{1,2,4,7};
		k=16;
		System.out.println(dfs(0,0));
	}
}

c++解法：

#include<iostream>
using namespace std;
const int maxn=20+10;
int arr[maxn];
int n,sum,k;
bool dfs(int i,int sum)
{
    if(i==n) return sum==k;
    if(dfs(i+1,sum)) return true;
    if(dfs(i+1,sum+arr[i])) return true;
    return false;
}
int solve()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>arr[i];
    }
    cin>>k;
    if(dfs(0,0))
        cout<<"Yes\n";
    else
        cout<<"No\n";
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    solve();
}

std::ios::sync_with_stdio(false);

百 度了一下，原来而cin，cout之所以效率低，是因为先把要输出的东西存入缓冲区，再输出，导致效率降低，而这段语句可以来打消iostream的输入 输出缓存，可以节省许多时间，使效率与scanf与printf相差无几，还有应注意的是scanf与printf使用的头文件应是stdio.h而不是 iostream。

 Lake Counting ( POJ No.2386)
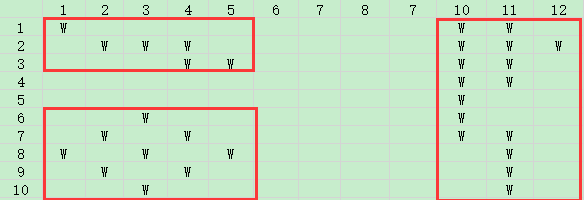
有一个大小为NXM的园子，雨后积起了水。八连通的积水被认为是连接在一-起的。请求出:园子里总共有多少水洼?(八连通指的是下图中相对W的*的部分)
  ***
  *w*

  ***

Sample Input

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
Sample Output

3

分析：因为是八联通，所以对角线的水也能够互相流通。如第一个水洼。

解析：

从任意的w开始，不停地把邻接的部分用' . '代替。1次DFS后与初始的这个w连接的所有w就都被替换成了' . '，因此直到图中不再存在w为止，总共进行DFS的次数就是答案了(感染法)。8个方向共对应了8种状态转移，每个格子作为DFS的参数至多被调用1次，所以复杂度为0(8 xNx M)=O(Nx M)。

[-1,0,1]

[-1,0,1]

两个for循环取这两个数组的值一共有9种可能，包括元素所在的位置偏移量（0，0），所以是可以遍历w周围的8个方向。

c++版本解法：

#include <cstdio>


using namespace std;


const int MAX_N = 110;

int n, m,res;
char field[MAX_N][MAX_N];

void dfs(int x, int y) {
    //将w感染成 . 
    field[x][y] = '.';
    //判断八个方向上是否有w
    for (int dx = -1; dx <= 1; dx++) {
        int nx = x + dx;
        for (int dy = -1; dy <= 1; dy++) {
            int ny = y + dy;
            if (nx >= 0 && nx < n && ny >= 0 && ny < m && field[nx][ny] == 'W')
                dfs(nx, ny);
        }
    }

}

void solve() {
    res = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if(field[i][j] == 'W') {
                dfs(i, j);
                res++;
            }
        }
    }

}


int main() {

    scanf("%d %d", &n, &m);

    getchar();  //吃掉换行符
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            scanf("%c", &field[i][j]);
        }
        getchar();
    }

    solve();

    printf("%d\n", res);

    return 0;
}

　Java版本解法：

package dfs;

import java.util.Scanner;

public class Main1 {
	static String[][] field;
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int m=sc.nextInt();
		field=new String[n][m];
		for (int i = 0; i < n; i++) {
			String tmp=sc.next();
			String tmps[]= tmp.split("");
			for (int j = 0; j < m; j++) {
				field[i][j]=tmps[j+1];
			}
		}
		System.out.println(solve());
	}
	private static int solve() {
		int res=0;
		for (int i = 0; i < field.length; i++) {
			for (int j = 0; j < field[0].length; j++) {
				if(field[i][j].equals("W")) {
					dfs(i, j);
					res++;
				}
			}
		}
		return res;
	}
	private static void dfs(int x, int y) {
		int n=field.length;
		int m=field[0].length;
		//将w感染成 . 
		field[x][y] = ".";
		//判断八个方向上是否有w
		for (int dx = -1; dx <= 1; dx++) {
			int nx = x + dx;
			for (int dy = -1; dy <= 1; dy++) {
				int ny = y + dy;
				if (nx >= 0 && nx < n && ny >= 0 && ny < m && field[nx][ny].equals("W"))
					dfs(nx, ny);
			}
		}
	}

}