并行计算架构和编程 | Assignment 4: cs149gpt and Lecture 10 - Efficiently Evaluating DNNs on GPUs

from pixiv 杉8

基础知识

Transformer and Attention

在上述课程中作者以卷积神经网络的卷积操作为例，告知我们可以将图片空间展开拉直为矩阵，将kernel(卷积核)也展开拉直为矩阵，如此用高效的矩阵乘法一次性计算所有输出，当然优化矩阵乘法的方式也有讲述：

循环变换／阻塞（blocking）
- 重排循环顺序，把深度／通道或空间分块，提升缓存命中率。
- 例如先对 jj,ii,kk 打小块（tile），保证权重和输入在 L1/L2 缓存里复用。其甚至给出了利用层次缓存进行分块的伪代码：
算子融合（Operator Fusion）
- 多个原本分开的算子（Operator）合并成一个算子来执行，从而减少中间数据的读写、降低调度开销、提升缓存命中率和并行效率。

对于上述内容我有许多曾感到困惑的地方：

卷积神经网络中什么是感受野？
如何理解将图片和卷积核拉直成大矩阵相乘？

推荐理解的视频和博客：

算子融合

算子融合（Operator Fusion），顾名思义，就是把多个原本分开的算子（Operator）合并成一个算子来执行，从而减少中间数据的读写、降低调度开销、提升缓存命中率和并行效率。下面分几个层面来聊：

背景：为什么需要算子融合？

在深度学习或一般的数值计算图中，我们往往会把模型拆成一系列基础算子（如卷积、批归一化、激活、逐元素加减、矩阵乘法、SoftMax……）。如果每个算子都独立执行，就会出现：

大量中间张量：算子 A 输出后写到内存，再读给算子 B，用完后再写下一个中间结果。
多次内存访存：读–写–读–写，数据在缓存／寄存器和主存之间来回搬。
重复指令派发：每个算子都要单独发 Kernel（在 GPU 上）或函数调用（在 CPU 上），控制／调度成本高。

核心思想

把若干个连续执行的算子“剪下来”，合并成一个更大的“fusion kernel”或“一次调度完成的复合算子”。

可以将算子融合本质上的优化想象为“生产者–消费者局部优化”（Producer–Consumer Locality Optimization）

其指的是在程序中，将“产生数据”和“使用数据”这两步紧密地安排在一起执行，以充分利用缓存或寄存器里的数据，从而减少内存访问开销、提升性能：

生产者（Producer）：负责生成或写入某段数据的代码区域。
消费者（Consumer）：负责读取或使用这段数据的代码区域。
局部优化：把本来分散在不同位置的“写入”与“读取”操作拉近，让它们在时间和空间上都更加“临近”，提高命中率，减少访存延迟。

这样做的直接好处是：

更少的内存读写
- 中间张量不落到主存/全局内存，直接在寄存器或 L1/L2 缓存里传递。
更少的调度开销
- 在 GPU 上，一次 Kernel 启动就把多步计算全部跑完；在 CPU 上，也减少函数调用和指令流开销。
更高的算力/带宽利用率
- 通过融合，还能更好地做矢量化、SIMD、算子级 blocking，使得硬件利用率提升。

怎么实现？（两条思路）

编译器/运行时自动融合
- 框架层面（TensorFlow XLA、TVM、PyTorch JIT 等）会在计算图优化阶段，图拆分、模式匹配、自动生成融合 Kernel。
- 用户写到前端只是 conv->bn->relu，底层会把它变成一个 CUDA kernel 或 LLVM IR 中的一段并行循环。
手写融合算子
- 库作者提前写好常用的融合实现（例如 cuDNN 就有 fusedConvBiasActivation），
- 用户或框架检测到模式后，直接调用更粗粒度的接口。

GEMM(General Matrix-Matrix Multiplication)

GEMM 是 “General Matrix-Matrix Multiplication” 的缩写，泛指通用的矩阵乘法运算。它在数值计算库（如 BLAS）里被定义为一个一级性能最优、最基础的接口，形式上通常写作：

\[C \;\leftarrow\; \alpha\,A\,B \;+\;\beta\,C \]

$A$ 是一个 $M\times K$ 的矩阵
$B$ 是一个 $K\times N$ 的矩阵
$C$ 是一个 $M\times N$ 的矩阵
$\alpha$、$\beta$ 是可选的标量系数

也就是说，GEMM 会

先计算 $\alpha\,A\,B$（标准的矩阵乘积，并乘以标量 $\alpha$）
再把结果加到 $\beta\,C$（将原来的 $C$ 按比例加回去）

GEMM = 通用矩阵乘法 + 累加，是线性代数中最核心、最能跑满硬件性能的操作。
在现代深度学习和科学计算中，无论是全连接层、卷积层（经 im2col 变形后）、还是注意力机制，底层都绕不开它。只要把问题“矩阵化”，就能调用高效的 GEMM 库来获得极致加速。

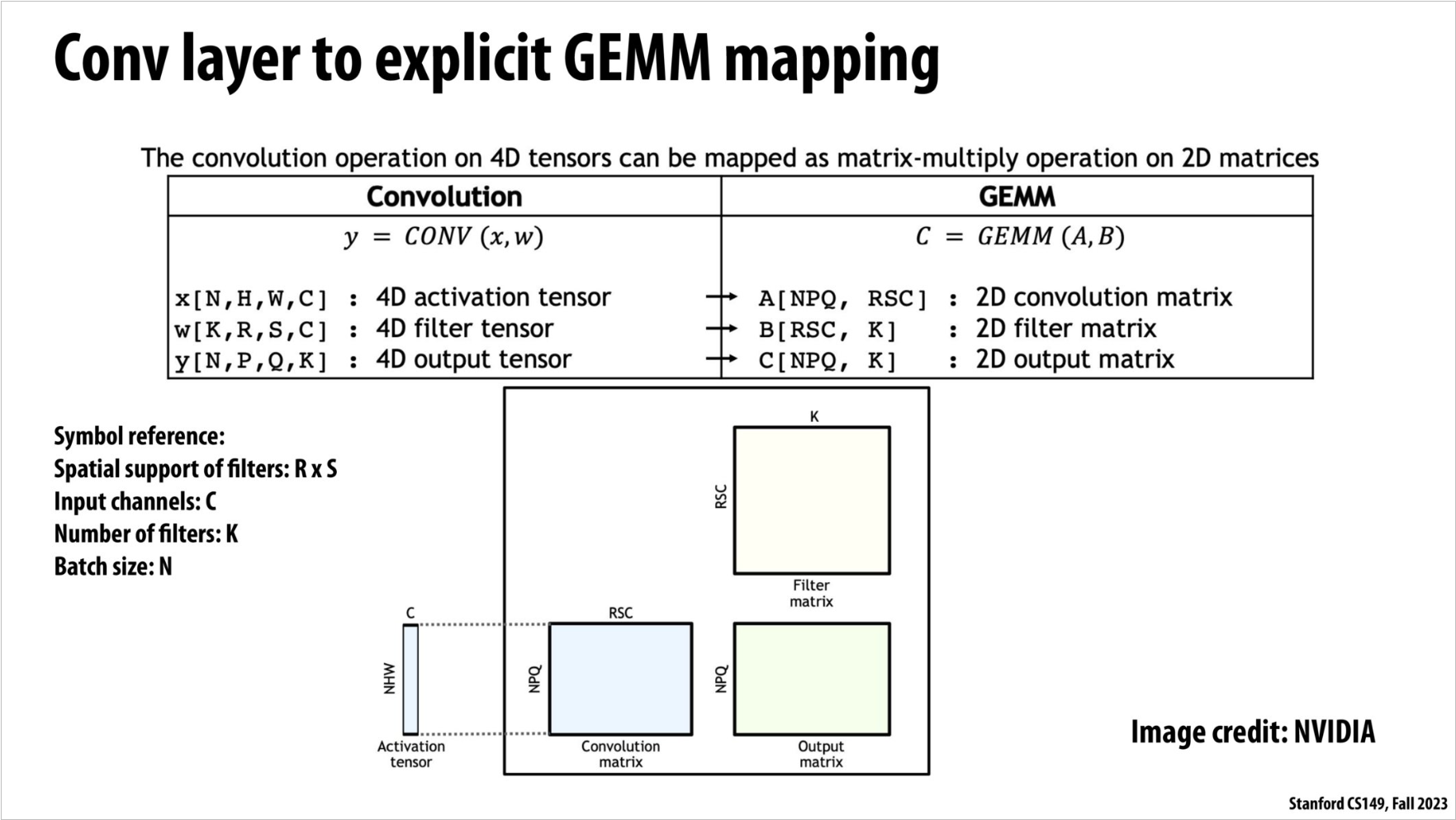
这张图想告诉你的，是“把 4 维卷积运算硬生生变成一个大矩阵乘法（GEMM）”，好处是可以直接调用 BLAS/GEMM 里极度优化好的例程来跑卷积。具体分三步看：

1. 原始 4D 卷积张量

Activation $x$ 是形状 $[N,H,W,C]$：
- $N$ 张图片，大小 $H\times W$，每个像素有 $C$ 个通道。
Filter $w$ 是形状 $[K,R,S,C]$：
- 一共 $K$ 个卷积核，每个核空间尺寸 $R\times S$，深度也和输入通道数 $C$ 一致。
Output $y$ 是形状 $[N,P,Q,K]$：
- 输出依然按批次 $N$，空间尺寸变成 $P\times Q$，通道数变为滤波器个数 $K$。

2. im2col——把卷积“拉平”成矩阵乘法

提取所有“Receptive Field”
- 每个输出位置 $(n,p,q)$ 都对应输入图上一个 $R\times S\times C$ 的小立方块（感受野）。
- 把这个立方块“拉平成”一个长度为 $R\times S\times C$ 的向量。
- 把所有 $N\times P\times Q$ 个位置的向量，按行堆成一张大矩阵
  
  \[ A\;:\;[\,N\!P\!Q\,,\;R\,S\,C\,] \]
拉平所有卷积核
- 每个卷积核 $k$（原来是 $R\times S\times C$）也拉平成一个同样长度的向量。
- 把这 $K$ 个向量按列拼成矩阵
  
  \[ B\;:\;[\,R\,S\,C\,,\;K\,] \]

3. 用 GEMM 计算 & 再 reshape 回去

矩阵乘法

\[ C \;=\; A \;\times\; B \quad\text{形状为}\quad [\,N\!P\!Q\,,\;K\,] \]
这里的 $C$ 就是所有 $(n,p,q,k)$ 的卷积结果，等价于逐点做乘加再加偏置的卷积。
再把 $C$ reshape 成 $[N,P,Q,K]$ 的输出张量，就和你本来在做的卷积一模一样。

$N$：Batch 大小
$H,W$：输入高／宽
$C$：输入通道数
$R,S$：卷积核高／宽
$K$：卷积核个数（输出通道数）
$P,Q$：输出高／宽（取决于 padding、stride）

“卷积 = im2col 把每个小块拉成行 → 拼大矩阵 A；把每个核拉成列 → 拼矩阵 B；然后做 C=A·B；再把 C reshape 回去。”

GPU 真的是做深度学习计算的最优解吗？

在做深度神经网络推理（DNN evaluation）的时候，你会发现在 GPU 上跑，虽然并行度很高，但每做一次“有意义”的乘加运算（比如一个 4×4 矩阵乘法），内核都要付出大量的“指令流控制”开销：

指令流（instruction stream）和调度开销

GPU 其实是一种“通用”并行处理器，每条微指令都要被抓取、译码、调度，然后才能驱动 ALU/乘加单元。
这些调度和控制本身要耗能、要占时间，对单次算力不直接做乘加，效率非常低。

复杂指令的思路：把控制开销“摊薄”

如果你只有简单的 FMA（一条指令做一个 $a\times x + b$），那一条指令的控制成本就只执行了一次乘加，控制 vs 计算比很高，导致能效低。
换成一条指令做 4 元向量点积（DP4：一条指令算完 $A_0B_0 + A_1B_1 + A_2B_2 + A_3B_3$），就相当于一次译码/调度可以干 4 次乘加，把控制能耗摊到 4 次算力上。
更高级的是一条指令做 4×4 矩阵乘并累加（MMA：一次发指令就算完 $C = A\cdot B + C$ 对 4×4 矩阵），一下子就能干 64 次乘加，把控制成本摊到 64 次计算上。

能效对比（相对 overhead）

纯“可编程”通用指令流（每条指令算一次简单操作）的开销基准：2000%（即控制能耗是算力能耗的 20 倍！）
半精度 FMA（每条指令做一次乘加）的 overhead 约 500%（控制仍然占了一大半能耗）
半精度 DP4（一次做 4 元点积）的 overhead 降到 500%/4≈125%（不过文中直接给出 500%，可能是参考了实际硬件的多余成本）
半精度 4×4 MMA（一次做 16 元乘加累加）的 overhead 仅 27%（控制开销已经被摊薄到接近零）

结论：为什么 GPU 不是最优

标准 GPU 指令集对通用图形／并行计算的调度开销很大，虽然可以用CUDA Tensor Core之类的指令做 MMA，但大多数逻辑还是要跑通用流水线。
DNN 推理最常用的就是大块矩阵乘加——如果你能用一条“重指令”搞定一整块运算，就大幅提升能效和吞吐。
因此，专用加速器（比如 Google 的 TPU、各种 NPU）会把 MMA 这样的复合指令做得更原生、更粗粒度，而不是让通用 GPU 的指令流去反复调度大量小操作。

指令流的控制/译码/调度 本身要消耗大量能量和时钟周期。
复杂／粗粒度指令（一次做多次乘加）能把这部分开销“摊薄”在更多计算上，提升能效。
标准 GPU 更偏向通用型，虽然有 Tensor Core，但整体架构仍需兼顾各种场景，推理场景下并不如定制化 DNN 加速器高效。

上述提到的三种常见的“算力指令”：

FMA（Fused Multiply–Add）:在一条指令里同时完成一次乘法和一次加法
DP4（4-element Dot Product）:对长度为 4 的向量同时做点积，一条指令计算
MMA（Matrix Multiply–Accumulate）:在一次指令里完成对固定尺寸（常见是 4×4、8×8、16×16 等）的小矩阵乘法并累加

FMA：将乘+加合并，最小粒度的优化。

DP4：中等粒度，一指令做 4 次乘加，常见于向量运算。

MMA：大粒度，一指令做整块小矩阵运算，是 AI 加速器如 TensorCore、TPU 的核心。

Lab

整个Lab其实就是在引导我们做GEMM（将图片拉直成大矩阵）和算子融合

Warm-Up: Accessing Tensors (3 Points)

我们可以打印下Tensor，看看pytorch中是如何规划放置tensor的

在深度学习和科学计算中，张量（tensor）就是多维数组的通用概念。

import torch

# 构造一个 shape 为 (2, 3, 4) 的三维张量
t = torch.arange(24).reshape(2, 3, 4)
print(t)
print("shape:", t.shape)

tensor([[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11]],

        [[12, 13, 14, 15],
         [16, 17, 18, 19],
         [20, 21, 22, 23]]])
shape: torch.Size([2, 3, 4])

import torch

t = torch.rand(2, 3, 3, 4)
print(t)
print("shape:", t.shape)

tensor([[[[0.8314, 0.8667, 0.6040, 0.7664],
          [0.6337, 0.4733, 0.9890, 0.7468],
          [0.8695, 0.1718, 0.7979, 0.9941]],

         [[0.5133, 0.1391, 0.3798, 0.2387],
          [0.0771, 0.2847, 0.0219, 0.2378],
          [0.7723, 0.8460, 0.1961, 0.3184]],

         [[0.1105, 0.3096, 0.7863, 0.8158],
          [0.2068, 0.7493, 0.5653, 0.4742],
          [0.0244, 0.1238, 0.3809, 0.6464]]],


        [[[0.0819, 0.0465, 0.5663, 0.3577],
          [0.1740, 0.3147, 0.9905, 0.1793],
          [0.9484, 0.4997, 0.4599, 0.1625]],

         [[0.1264, 0.3042, 0.5510, 0.8706],
          [0.1198, 0.4451, 0.4345, 0.9289],
          [0.9008, 0.7202, 0.8848, 0.7727]],

         [[0.5925, 0.1414, 0.1041, 0.9140],
          [0.4543, 0.1446, 0.3256, 0.7705],
          [0.6384, 0.6177, 0.7801, 0.3177]]]])

可以发现其实tensor就是在不断地"套娃"

Briefly describe how a 4D tensor/array is laid out in memory. Why do you think this convention was chosen and how does it leverage hardware?

我们知道我们处理2Dtensor时是将其拉直成一维，然后一行一行连续地存放到内存中，4Dtensor的处理方式也是一样的。

Part 2: Blocked Matrix Multiply and Unfused Softmax (20 Points)

这里分块的实现思路在课件PPT中给出了伪代码：

What was the optimal tile size for your matrix multiplications? Explain why you think this tile size worked best for your implementation.

--------------------------------------------

tile size = 32

REFERENCE - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  140.308ms
mem usage:  4718592 bytes

STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  141.917ms
mem usage:  4718592 bytes

--------------------------------------------

tile size = 16

REFERENCE - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  140.28ms
mem usage:  4718592 bytes

STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  129.777ms
mem usage:  4718592 bytes

-----------------------------------------------

tile size = 12

REFERENCE - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  139.712ms
mem usage:  4718592 bytes

STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  128.541ms
mem usage:  4718592 bytes

-----------------------------------------------

tile size = 8

REFERENCE - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  139.802ms
mem usage:  4718592 bytes

STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  117.61ms
mem usage:  4718592 bytes

-----------------------------------------------

tile size = 4

REFERENCE - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  141.043ms
mem usage:  4718592 bytes

STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  136.841ms
mem usage:  4718592 bytes

-----------------------------------------------

tile size = 2

REFERENCE - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  140.17ms
mem usage:  4718592 bytes


STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  188.673ms
mem usage:  4718592 bytes

---------------------------------

我有如上测试数据，可知机器给我的答案是我在tile size为8时性能最好

对于这个答案我也比较意外，因为我的这台机器：

cache line 64B
float 4B

所以一个cache line可以保存16个float元素，如果tile size为16，那么tile block的一行正好可以装满一个cache line能够充分利用到缓存

For a matrix multiply of Q(Nxd) and K_T(dxN), what is the ratio of DRAM accesses in Part 2 versus DRAM acceses in Part 1? (assume 4 byte float primitives, 64 byte cache lines, as well as N and d are very large).

DRAM即是内存（SRAM是缓存）

因为N和d都被假设很大，那么对于Part 1在访问Q的一行时需要访问$\frac{d}{16}$次内存（除以16是因为一个cache line能够保存16个float元素）

在访问K_t的一列时（即访问K的一行时），需要访问$\frac{d}{16}$次内存

然后还需要访问一次内存将计算出来的数据写到QK_t中

总共要经历$（\frac{d}{16} ＋ \frac{d}{16} ＋ 1）* N * N$次内存访问

然而Part 2总共要经历的内存访问次数为 $({2 * tileSize ＋ 1}) * \frac{d}{16} * \frac{d}{16} $

Part 3: Fused Attention (25 Points)

Parallelizing with OpenMP

OpenMP的英文全称是Open Multiprocessing

MPI, OpenMp, CUDA，Triton之间的关系和区别是什么？

Triton 又名 OpenAI Triton，是一种专门为深度学习、自定义 GPU 内核优化而设计的编程语言／编译框架。它与 MPI、OpenMP、CUDA 的关系和区别，可以从以下几个方面来看：

框架	并行范式	主要用途
MPI	分布式内存消息传递	跨多台机器的分布式计算
OpenMP	共享内存多线程	单机多核 CPU 并行
CUDA	异构计算（GPU）	在 NVIDIA GPU 上写低级、细粒度并行核函数
Triton	GPU SPMD（Python 嵌入式）	更高层次地编写、优化深度学习／张量运算内核

MPI、OpenMP 主要针对 CPU 端的并行（分别是跨节点和多核），
CUDA 和 Triton 都是 GPU 编程，但 CUDA 更偏底层、C++ 拓展，而 Triton 通过 Python+JIT 提供了更高生产力的接口。
MPI
- 典型硬件：多台物理节点（集群），每节点可多核。
- 适合大规模分布式计算（数十、数百乃至上千个节点），跨节点通信代价高。
OpenMP
- 典型硬件：单台多核 CPU。
- 适合中小规模并行（通常几十乃至上百个线程）。
- 利用共享内存，线程间通信（读写共享变量）效率高。
CUDA
- 典型硬件：NVIDIA GPU。
- 擅长海量数据并行、SIMD／SIMT 风格的细粒度并行。
- 数千—上万个 GPU 线程同时执行，但需要将数据从主机（CPU）拷贝到设备（GPU）。

Why do we use a drastically smaller amount of memory in Part 3 when compared to Parts 1 & 2?

因为通过算子融合我们可以少存储许多中间矩阵比如QK_t

Comment out your #pragma omp ... statement, what happens to your cpu time? Record the cpu time in your writeup. Why does fused attention make it easier for us utilize multithreading to a much fuller extent when compared to Part 1?

REFERENCE - FUSED ATTENTION statistics
cpu time:  48.769ms
mem usage:  557056 bytes


STUDENT - FUSED ATTENTION statistics
cpu time:  48.537ms
mem usage:  557056 bytes


在gpt149.py中设置了

NUM_THREADS=8
    #part 3
    def myFusedAttention(self):
        if self.isRef:
            with record_function("STUDENT - FUSED ATTENTION"):
                temp = torch.zeros((NUM_THREADS, self.N))
                out = mr.myFusedAttention(self.Q, self.K, self.V, temp, self.B, self.H, self.N, self.d)
            return out
        with record_function("REFERENCE - FUSED ATTENTION"):
            temp = torch.zeros((NUM_THREADS, self.N))
            out = ms.myFusedAttention(self.Q, self.K, self.V, temp, self.B, self.H, self.N, self.d)
        return out


去掉之后：
STUDENT - FUSED ATTENTION statistics
cpu time:  208.506ms
mem usage:  557056 bytes

因为fused attention让外循环B, H, N之间成为数据独立的了

Part 4 : Putting it all Together - Flash Attention (35 Points)

这里我踩了了个大坑，就是ref算法是按照上述伪代码实现的，因为float计算是很敏感的，所以我们实现的时候一定要按照上述伪代码算法的顺序实现，比如不能将for 1<＝j<＝T_c和for 1<＝i<＝T_r的顺序给调换

How does the memory usage of Part 4 compare to that of the previous parts? Why is this the case?

STUDENT - FLASH ATTENTION statistics
cpu time:  164.284ms
mem usage:  524288 bytes

对比Part 3

STUDENT - FUSED ATTENTION statistics
cpu time:  48.537ms
mem usage:  557056 bytes

对比Part 2

STUDENT - BLOCKED MATMUL + UNFUSED SOFTMAX statistics
cpu time:  117.61ms
mem usage:  4718592 bytes

会发现Part 4的实现方式使用内存是最小的，因为我们在Part 4中即使使用到了一些中间矩阵，但是这些中间矩阵的大小也是tileSize级别的，较小

通过算子融合和tile block的技术实现的Flash Attention充分利用了生成者-消费者局部性优化的技术，不仅减少了内存访问，同时也使用了更少的内存

Notice that the performance of Part 4 is slower than that of the previous parts. Have we fully optimized Part 4? What other performance improvements can be done? Please list them and describe why they would increase performance.

我们还可以对外循环使用多线程来优化，对内循环可以使用并行指令来优化

posted @ 2025-05-31 19:25 次林梦叶阅读(121) 评论(0) 收藏举报

刷新页面返回顶部

次林梦叶的小屋

音无结弦之时