深度学习 Deep Learning | 基于 3Blue1Brown 教学的总结

神经网络的结构
这里作者先从神经网络初始最著名的应用--识别手写数字图片中的数字为例,讲解神经网络的基本架构:

我们将一张图片中的全部像素展开为一列,每一个像素就是初始输入神经元中的值
这上述角度,我们可以神经元看成“装有数字的容器”,里面的数字是“激活值”
其值越大该神经元激活的程度就越大。最后一层神经元的激活值可以认为是整个神经网络认为是该输出值的可能性,激活值越大,是该值的可能性越大。
上一层的激活值影响并决定下一层的激活值,所以神经网络的核心就是一层的激活值通过怎样的运算,算出下一层的激活值。
那么上一层的激活值到底如何影响下一层的激活值的呢?
通过神经元之间的“连线”,这些“连线”即是上一层神经元对下一层神经元的权重
这里作者以图像识别为例,讲解一下如何理解这个权重:
下一层的神经元可以看做对上一层神经元的信息压缩,我们以第一层神经元和第二层神经元为例:
在图像识别中,第一层神经元的激活值是像素值,那么第二层神经元的激活值可以看成图像某一块区域的总像素值,比如如果第二层某个神经元的激活值很高,很可能说明其代表的区域有笔画出现

例如在如上图片中,我想要知道纯白区域是否存在一条横线? 假设代表上图纯白区域的第二层某个神经元如下图:
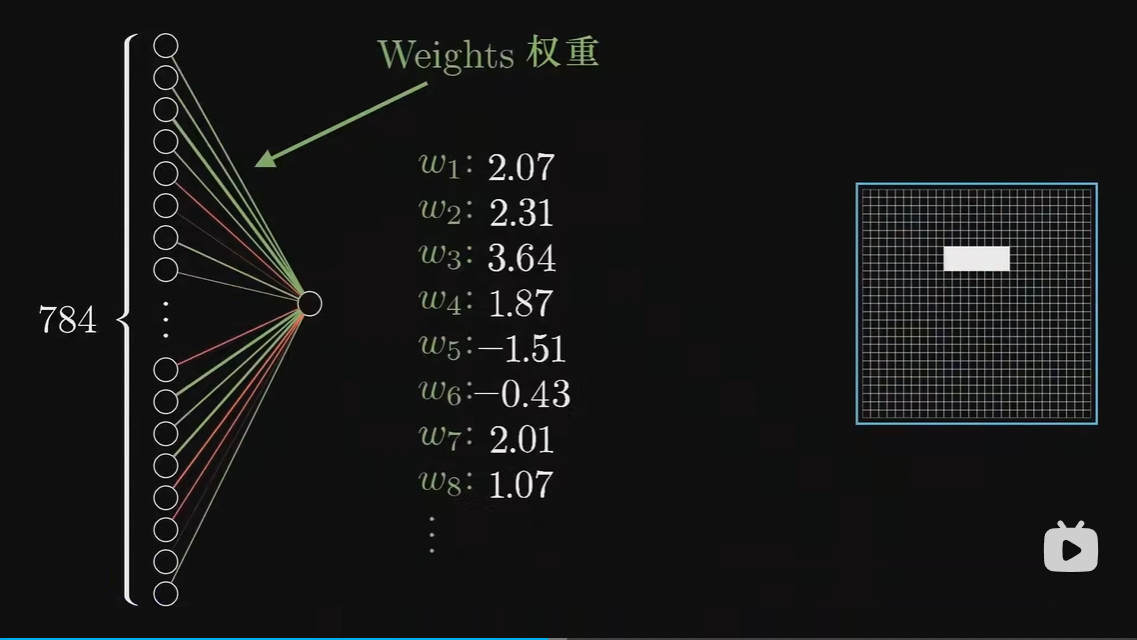
那么我们可以通过设置权重,让第一层在纯白区域的神经元连向第二层某个神经元的权重都为正值,其余第一层神经元连向第二层某个神经元的权重都为零,那么可以让代表纯白区域的第二层某个神经元激活值很大,即表示纯白区域是否存在一条横线!

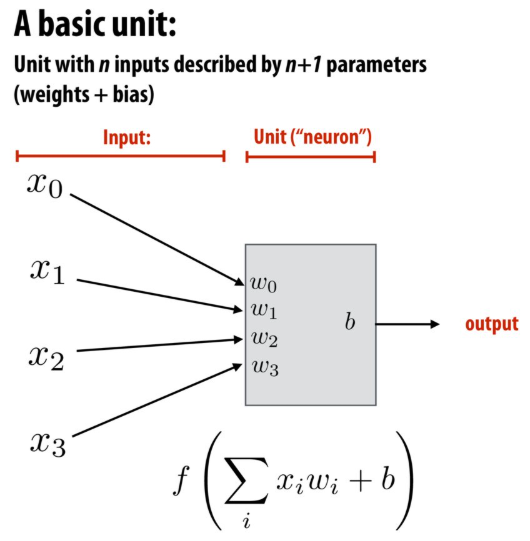
从上一层神经元到底下一层某个神经元除了权重外,还有一个参数b(偏置Bias).
偏置存在的意义是设置一个阈值,当超过偏置值激发才是合理的.
权重和偏置都是通过训练出来的
从上述数学角度思考,神经元看作一个函数更加准确。他的输入是上一层所有神经元的输出,输出是一个0到1之间的值。
深度学习之梯度下降法与反向传播
梯度下降法
对于上述的神经网络,我们需要一个方法来判断这个网络是否算好?
我们定义损失函数和代价函数:
-
损失函数(Loss Function)——针对单个样本的误差
-
通常记作 \(L(\hat y, y)\),它衡量了模型对单个样本 \((x, y)\) 的预测 \(\hat y\) 与真实标签 \(y\) 之间的差距。
-
常见示例:
- 均方误差(MSE): \(L(\hat y, y)=\tfrac12\|\hat y - y\|^2\)
- 二元交叉熵: \(L(\hat y, y)=-\bigl[y\ln\hat y + (1-y)\ln(1-\hat y)\bigr]\)
- 多分类交叉熵: \(L(\hat y, y)=-\sum_{k}y_k\ln\hat y_k\)
-
对于我们上述的神经网络,最终输出有多个神经元,所以单个样本的预测结果\(\hat y\)是个向量,同样真实标签 \(y\)也是个向量
-
代价函数(Cost Function)——针对整个训练集的平均误差
-
通常记作 \(J(\theta)\) 或 \(J(W,b)\),它是把所有训练样本上的损失累加(或取平均)得到的整体度量:
\[ J(\theta) = \frac{1}{m}\sum_{i=1}^m L\bigl(\hat y^{(i)},\,y^{(i)}\bigr), \]其中 \(m\) 是训练样本总数,\(\theta\) 代表模型参数(如网络的所有权重和偏置)。
-
通过最小化代价函数 \(J(\theta)\),我们同时最小化了所有样本的平均损失。
-
在视频中作者将代价函数简写为 \(C\), 那么接下来的公式推导我们也将代价函数简写为 \(C\)
对于上述的神经网络,我们可以将其整体看做一个函数:
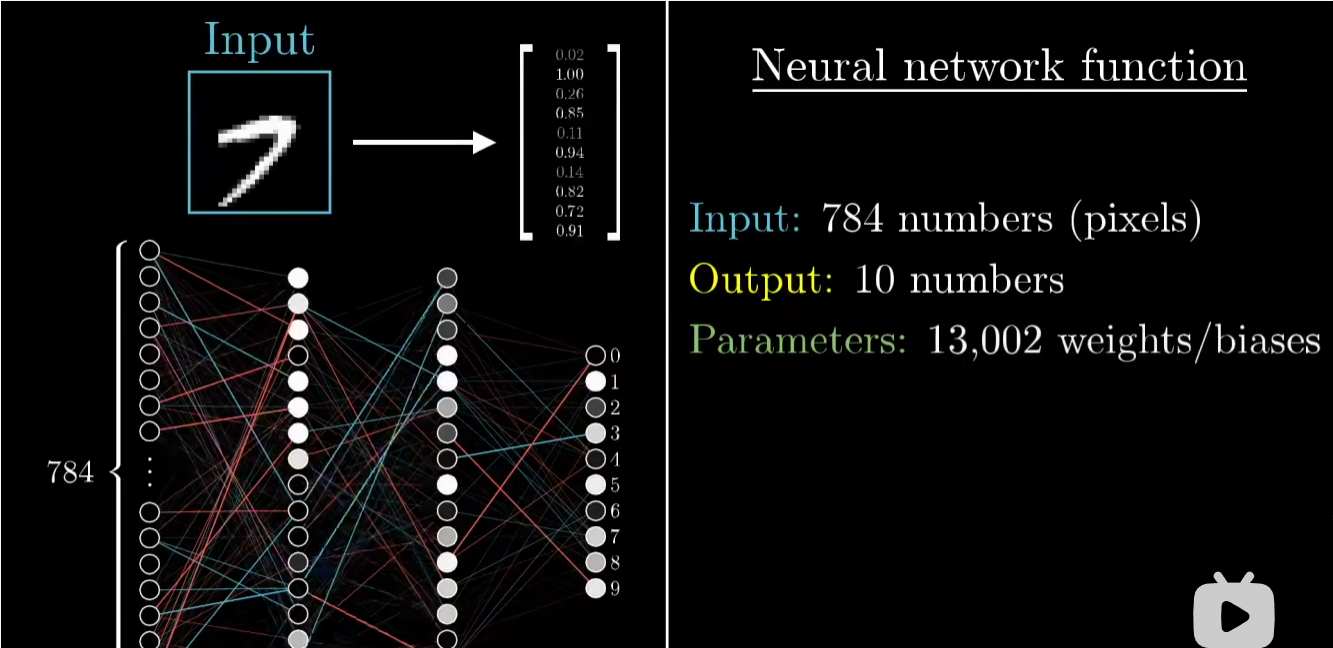
即输入为全部像素点值,输出为预测0-9数字的概率值,参数为全部权重和偏置值
对于代价函数,我们同样也可以将其整体看做一个函数:

即输入为全部权重和偏置值,输出为一个数值评价网络的好坏,参数为全部的样本
我们当然是希望代价函数的输出越小越好,那么如何让代价函数的输出越小呢?
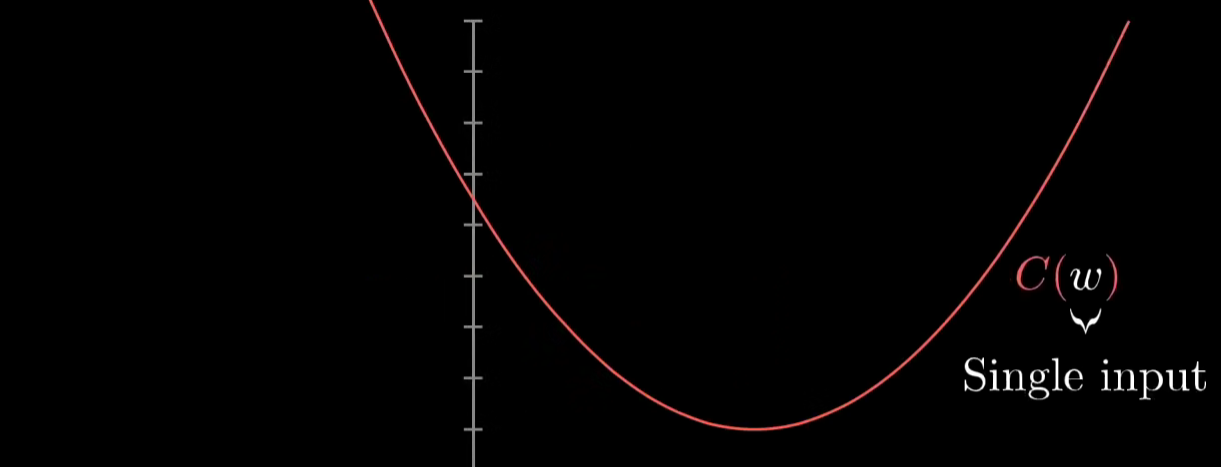
作者提到简化思考,我们先不去想复杂的大量的输入,而是将其简化为只有一个输入:
||
||
V
想一想我们如何通过找到一个值w,使得 \(C(w)\)最小呢?
-
求导直接算出来?\(\frac{dC}{dw}(w) = 0\), 当函数过于复杂时我们并不能一定算出来
-
一个好的方法是先随机挑选一个点w, 然后求在w时的斜率:
- 当斜率为正,说明我们要让w向左(w变小)走才能让\(C(w)\)变小
- 当斜率为负,说明我们要让w向右(w变大)走才能让\(C(w)\)变小
其实上述中的斜率是在一维下梯度的一个特殊概念,我们以二维为视角讲解下梯度:

对于一个标量函数 \(C(x, y)\),它的梯度记作:
这个梯度向量:
- 函数的梯度决定了函数最陡的增长方向,它的负数代表的就是下降最快的方向
- 梯度向量的长度就代表了这个最抖的斜坡到底有多抖
知晓了上述内容,我们的目的其实就变成了对代价函数求解其梯度,根据梯度的方向和大小来改变权重/偏置值 (我们希望梯度下降地最快),即:
Compute ∇C
Small step(W权重 or B偏置) in -∇C direction
Repeat

反向传播
那么问题又变成了我们如何计算代价函数\(C\)对每一个变量w/b的梯度呢?
梯度的计算方式为:\(\frac{\partial C}{\partial W}\) ,这里我们的困难主要是要求出代价函数 \(C\) 对每一个变量w/b的梯度
我们现在来简化问题,我们先假设我们的训练样本只有1个,我们也假设每一层的神经元只有一个,那么上述的神经网络可以简化为如下:
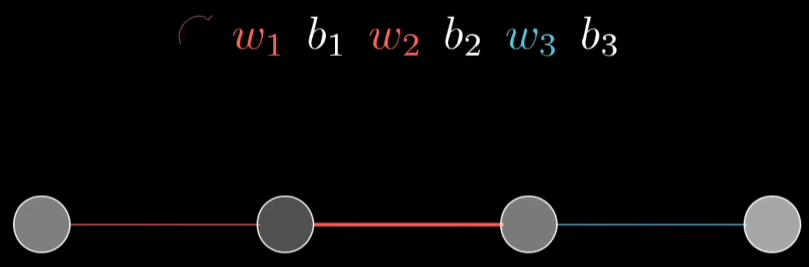
图上这个网络就是由3个权重和3个偏置决定的
作者也提到可以从代价函数对w,b这些变量有多敏感来理解梯度,例如\(\partial W\)可以看做对W的微小扰动,\(\partial C\)可以看做W对C的扰动,那么\(\frac{\partial C}{\partial W}\)就可以看做C对W微小变化有多敏感
接下来我们主要讲解对w进行求梯度的方法,对于b方法是一样的:
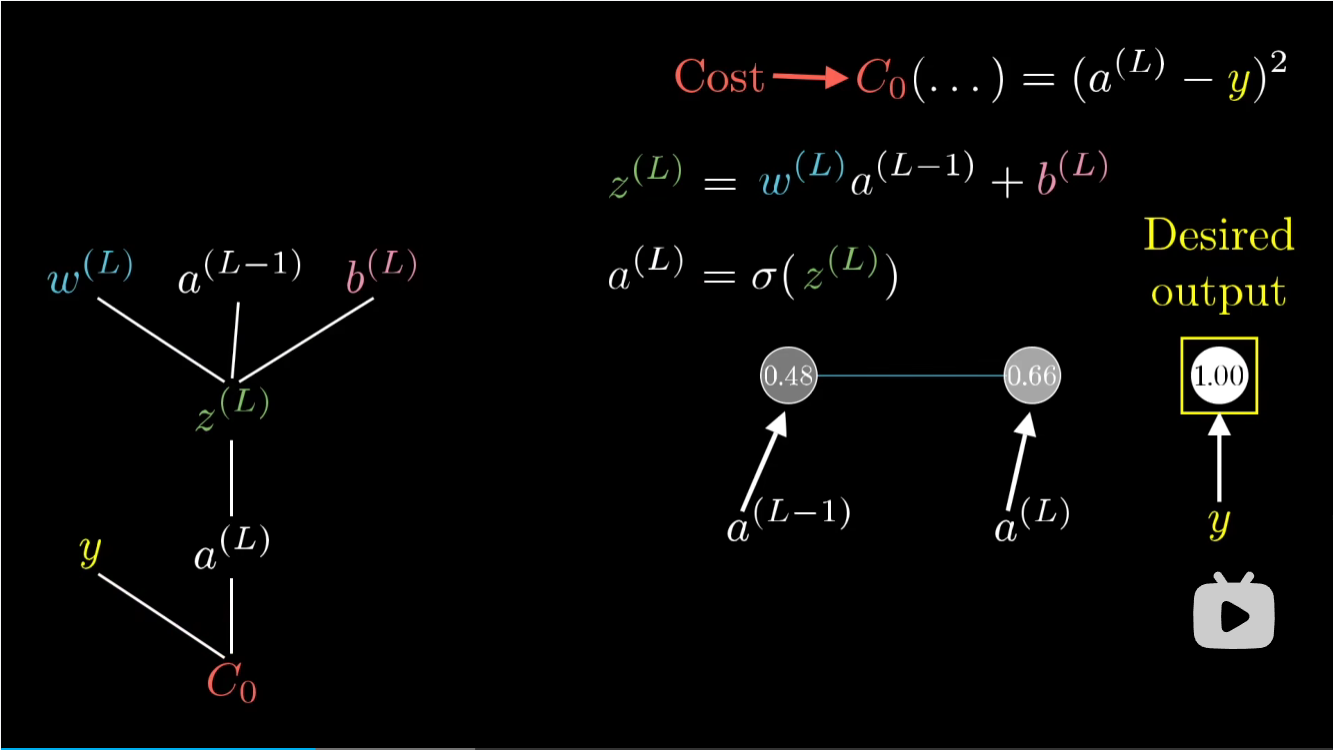
依据链式法则:\(\frac{\partial C_{0}}{\partial w^{L}} = \frac{\partial z^L}{\partial w^{L}} \frac{\partial a^L}{\partial z^{L}} \frac{\partial C_0}{\partial a^{L}}\)
我们定义误差项\(\delta^l_j\)
\(\delta^l_j\) 就是“第 \(l\) 层第 \(j\) 个神经元的净输入 \(z^l_j\) 变化对总损失的影响”。
因为我们这里每层只有一个神经元,所以我们直接定义\(\delta^l\)
对于输出层(第 \(l\) 层),我们有:
- \(\nabla_{a^l} C = \frac{\partial C}{\partial a^l}\) 是代价函数对网络输出的梯度;
- \(\sigma'(z^l)\) 是激活函数在 \(z^l\) 点的导数;
- “\(\circ\)” 表示逐元素相乘(Hadamard 乘积)。
即:
所以链式法则我们可以写成:$$\frac{\partial C_{0}}{\partial w^{l}} = \delta^l \frac{\partial z^{l}}{\partial w^{l}}$$
现在我们求出代价函数\(C_0\)对\(w^l\)的梯度了,为了更新全部的\(w\),我们接着需要求\(\frac{\partial C_{0}}{\partial w^{l-1}}\),按照链式法则我们可以得出:
经过上述特殊案例,我们可以先感受下如下结论:
对于 \(l=L-1,L-2,\dots,1\),误差项由后一层 \(\delta^{l+1}\) 反向传播过来:
所以既然在我们这个案例中\(\delta^{l-1} = \delta^{l} w^l \sigma'(z^{l-1})\),想必\(\frac{\partial C_{0}}{\partial w^{l-2}}\)之类的也很好算出来了
现在我们总结下:
至此,我想要总结下整个反向传播的步骤了:
-
前向传播
- 对当前批次中每个样本,依次计算每层的 \(z^l, a^l\) 并缓存下来。
-
计算输出层误差 \(\delta^L\)。
-
反向传播误差
- 对 \(l=L-1\) 到 \(1\),递推计算 \(\delta^l\)。
-
计算梯度累加
- 累加本批次所有样本的 \(\delta^l (a^{l-1})^T\) 和 \(\delta^l\)。
-
参数更新
\[W^l \;\gets\; W^l - \frac{\eta}{B}\sum_{i\in\text{batch}}\delta^{l\,(i)}(a^{l-1\,(i)})^T,\quad b^l \;\gets\; b^l - \frac{\eta}{B}\sum_{i\in\text{batch}}\delta^{l\,(i)}. \]
其中,\(\eta\) 为学习率,\(B\) 为小批量样本数。
注意上述我们说的小批量样本数,我们这里使用的是小批量梯度下降(Mini‐Batch GD)或称为随机梯度下降(SGD)
我们有对单个样本的反向传播的方式,即对每个样本计算代价函数对w/b的梯度,反向传播一次更新全部的w/b
但是这种方式对于多训练数据(Batch)下计算量太大了,于是我们就有了随机梯度下降(SGD):
对于 𝑚个样本的全量(Batch)梯度:
- 将训练集分成若干个小批次(比如每批 \(B\) 个样本),对每个小批次重复批量下降的过程,从而加快收敛并增加随机性以跳出局部极小。
- 当 \(B=1\) 时,等价于经典的随机梯度下降。
什么叫做对每个小批次重复批量下降的过程?
即对于这一小批次中的每个样本,计算出代价函数对每个w/b的梯度,但是先不更新梯度。
等算出这一小批次中全部样本中代价函数对每个w/b的梯度,比如对于代价函数\(C\)对于 \(w_{1}\)的梯度,我们得到了B个样本中的代价函数\(C\)对于 \(w_{1}\)的梯度:$ \nabla C(w_1)_1, \nabla C(w_1)_2,..., \nabla C(w_1)_B$, 然后将这些梯度累加求平均得到的数值 \(Avg\nabla C(w1)\) 去更新\(w_1\)
好了,接下来让我们来考虑下更复杂的情况,假设神经网络的每一层并非只有一个神经元:
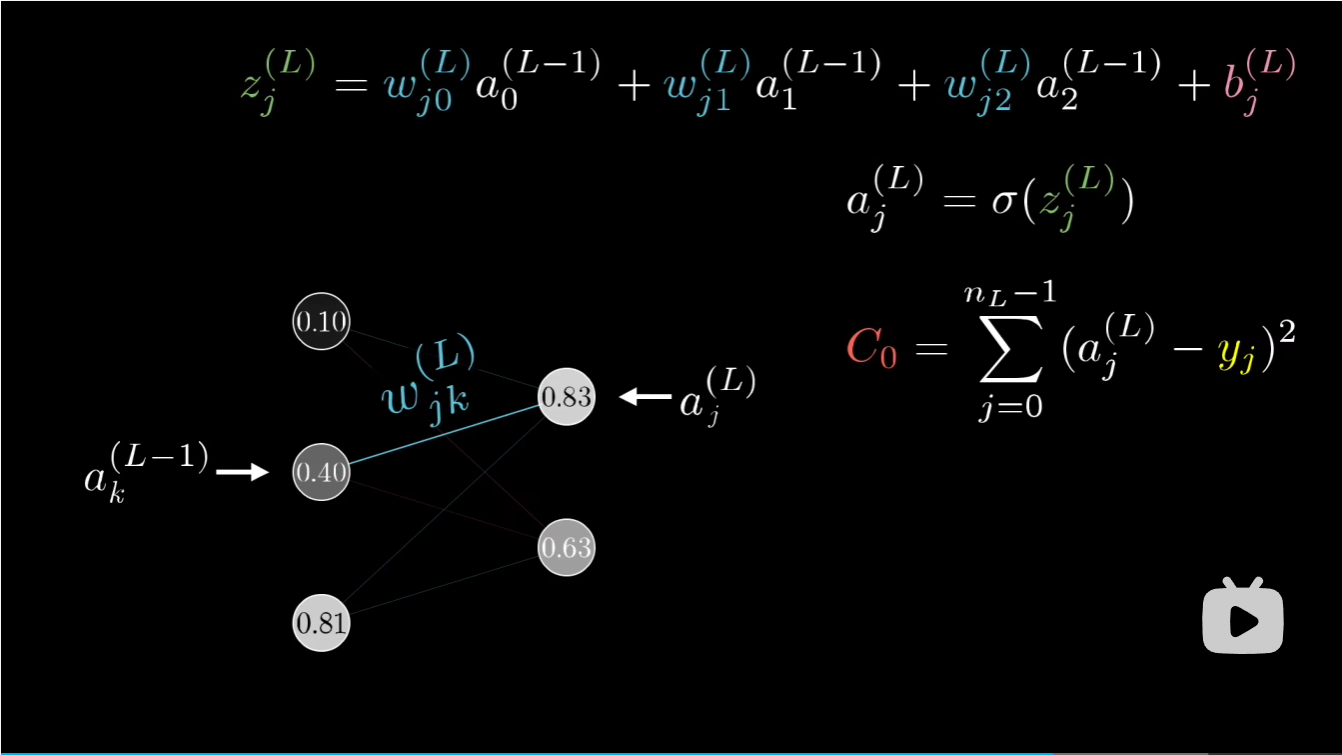
我们想要求出\(\frac{\partial C_0}{w^{l}_{jk}}\)
按照老套路我们需要有损失项:
需要注意的是从\(C_0\)到\(a^{l}_{j}\)这条路径上会有"分支",即在第\(l+1\)层中有许多神经元是依赖\(a^{l}_{j}\)的,如下图可能会帮助理解:
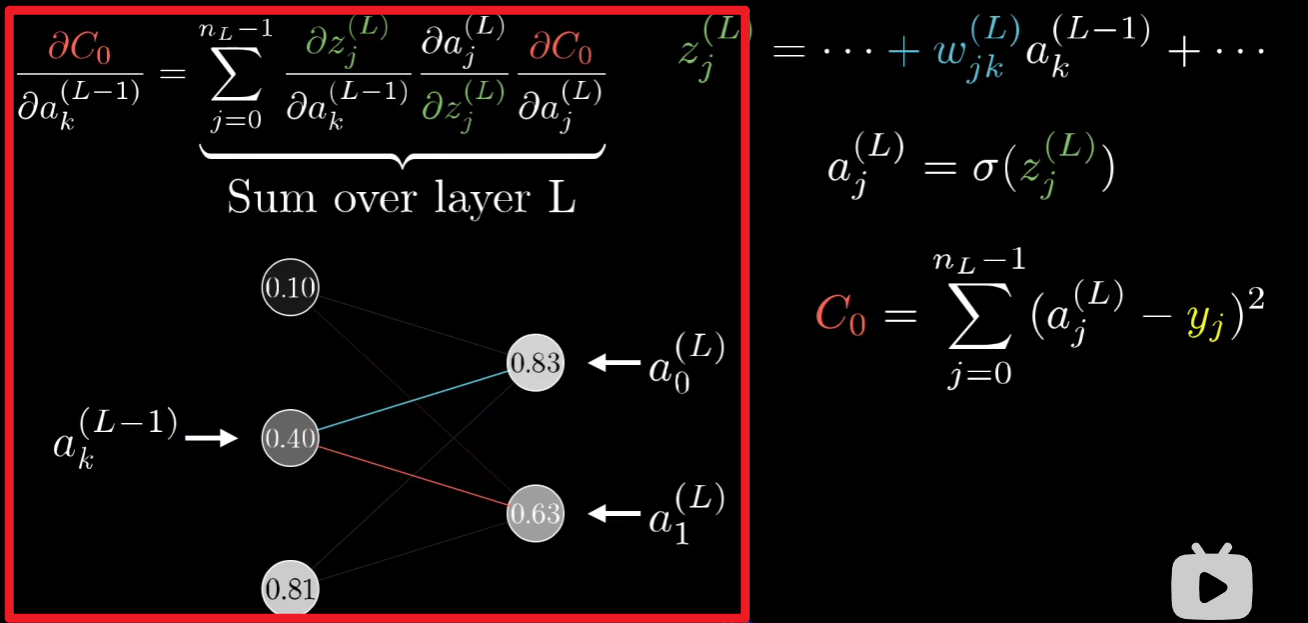
所以这里我假设神经网络每一层是全连接的,那么
所以你依旧能够看到结论是对的:
对于 \(l=L-1,L-2,\dots,1\),误差项由后一层 \(\delta^{l+1}\) 反向传播过来:
GPT, Transformer, Attention
GPT 是基于 Transformer 架构,并使用 Attention 机制 的一种语言模型。
Transformer 是 Google 在 2017 年提出的一种完全基于 Attention 机制的架构,不再依赖 RNN 或 CNN。
构成:
- Encoder(编码器)层
- Decoder(解码器)层
- 每层包含:Multi-Head Attention + Feed Forward + Layer Norm + 残差连接
Attention机制(注意力机制)——最底层的基础模块
Attention 是一种让模型“关注”输入序列中重要部分的机制。它的本质是加权求和,权重由相关性决定。
接下来我们主要讲解的是self-attention:
- Self-Attention(自注意力):输入是同一序列中的每个位置彼此计算注意力(Transformer核心)
- Cross-Attention:两个序列之间的注意力计算(如翻译任务中,源语言对目标语言)
GPT(Generative Pre-trained Transformer)——具体实现的语言模型
GPT 是 OpenAI 提出的基于 Transformer Decoder 的语言模型,强调 生成式建模(预测下一个词)。
- 使用 Transformer 的 Decoder 部分
- 只使用 Masked Self-Attention(防止看到未来的词)
- 先在大规模文本上预训练,再微调
GPT首先第一层和最后一层分别是Embedding 和 Unembedding
Embedding and UnEmbedding

首先需要训练出一个12288维度(行),~50k列的词嵌入矩阵,对于每一行文本,我们都将其进行切分成各个token, 依据Embedding matrix将每个token对应到一个词向量
我们可以把Embedding matrix 是一个查表工具,用来把每个词转换成一个固定维度的向量,使得神经网络可以理解和处理语言。
初始,同一个token可能是一样的词向量,经过Attention机制后,能够依据上下文更新词向量
在词向量的维度空间中方向可以代表语义
当模型生成文本时,它的输出是一个向量(比如隐藏层输出),但我们最终想要的是一个词 —— 那么必须把这个向量映射回词表,选择最可能的词。
这个映射就靠 unEmbedding matrix 实现
Attention
Attention 就是在 Query 和一组 Key 之间计算相关性,然后根据相关性加权求和对应的 Value。
这里先提供ChatGPT回答我的答案:具体讲讲Attention中的Query, Key,Value
🔍 背景:为什么需要 Attention?
在 NLP 中,比如翻译或生成文本,模型需要“决定”当前生成的词要关注输入句子的哪些部分。注意力机制就是用来做这种“关注”决策的工具。
🧩 一、Query、Key、Value 是什么?(类比 + 数学)
📌 类比:图书馆找书
- Query(Q):你现在的需求(比如“我想找讲 Transformer 的书”)
- Key(K):每本书的主题标签(比如“Transformer”、“CNN”、“RNN”)
- Value(V):每本书的具体内容
你根据当前需求(Query)和每本书的主题(Key)算出匹配度,然后从书架中提取出匹配度高的内容(Value)作为重点阅读材料。
🔣 二、计算流程(以 Self-Attention 为例)
设输入序列是多个词的向量表示,每个词向量都通过学习得到对应的:
Query向量Key向量Value向量
这些向量由以下公式计算:
其中:
- \(X\) 是输入序列的矩阵(如每个词的 embedding)
- \(W^Q, W^K, W^V\) 是需要学习的参数矩阵
🔁 三、Attention 的数学过程
给定一组 Query(Q)、Key(K)、Value(V),我们计算 Attention 输出:
步骤解释:
- QKᵀ:计算每个 Query 和所有 Key 的点积,表示相关性
- 除以 √dk:防止数值过大,稳定梯度
- softmax:归一化为权重(所有相关性加和为 1)
- 乘 V:用这些权重对 Value 向量加权求和
🎯 结果:
Attention 的输出是当前 Query 下,对所有 Value 的“加权平均”,权重就是它和每个 Key 的相似度。
🤔 举个小例子:
假设输入句子是 “The animal didn't cross the street because it was too tired.”
- 当前想生成词 “it” 所代表的词是谁?
- 模型会把 “it” 的向量作为 Query,句子里其他词(比如 “animal”, “street”)变成 Key 和 Value
- 计算相似度后发现 “animal” 是最相关的 Key
- 所以 Attention 输出向量是来自 “animal” 对应的 Value,加权求和结果更“靠近” animal 的语义
🧠 总结
| 元素 | 含义 |
|---|---|
| Query | 当前词或位置的“提问” |
| Key | 所有词的“标签” |
| Value | 所有词的“内容” |
| 输出 | 当前词应关注的加权信息(从 Value 得到) |
3Blue1Brown的理解
Query

Key

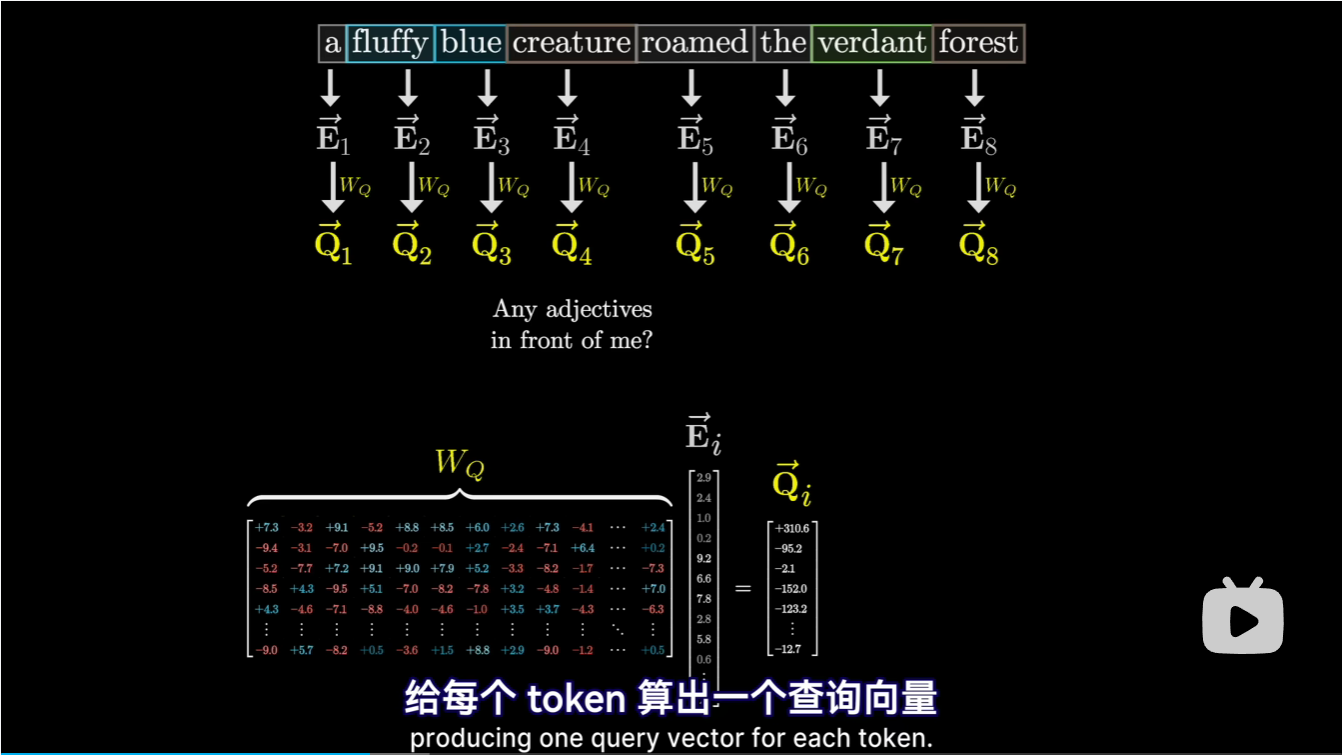
需要注意一下这里的维度信息,在这个案例中,\(W_Q\)是128维(128行),12288列的矩阵;而词向量\(\vec{E_i}\)为12288x1的向量;所以\(\vec{Q_i}\)为128x1的向量
我们同样有\(W_K\)矩阵128x12288,与每个词向量\(\vec{E_i}\)相乘,得到\(\vec{K_i}\)
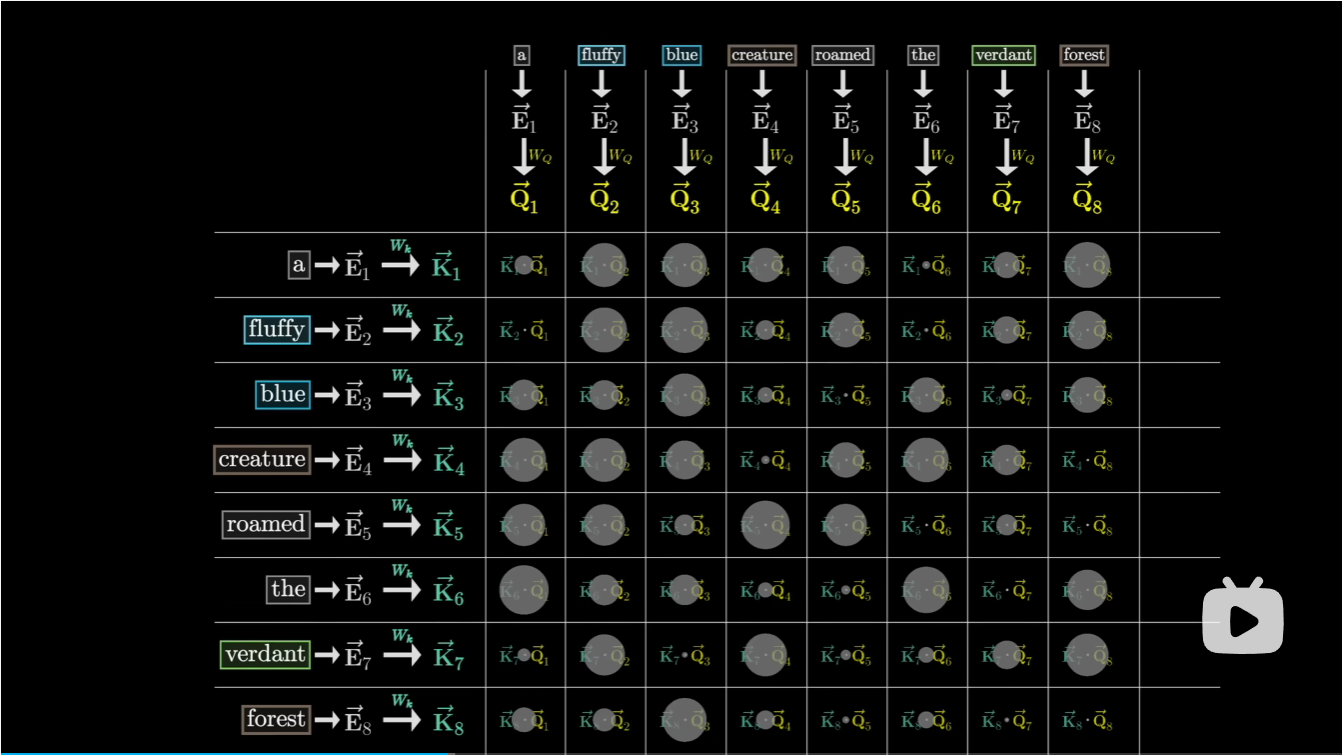
然后每个\(\vec{Q_i}\)与\(\vec{K_i}\)点积得到,其中点积得到的值越大,说明Q和K越匹配
然后我们对这张相关度表中的每一列取softmax, 表示左侧的键与顶部查询的相关度

Value
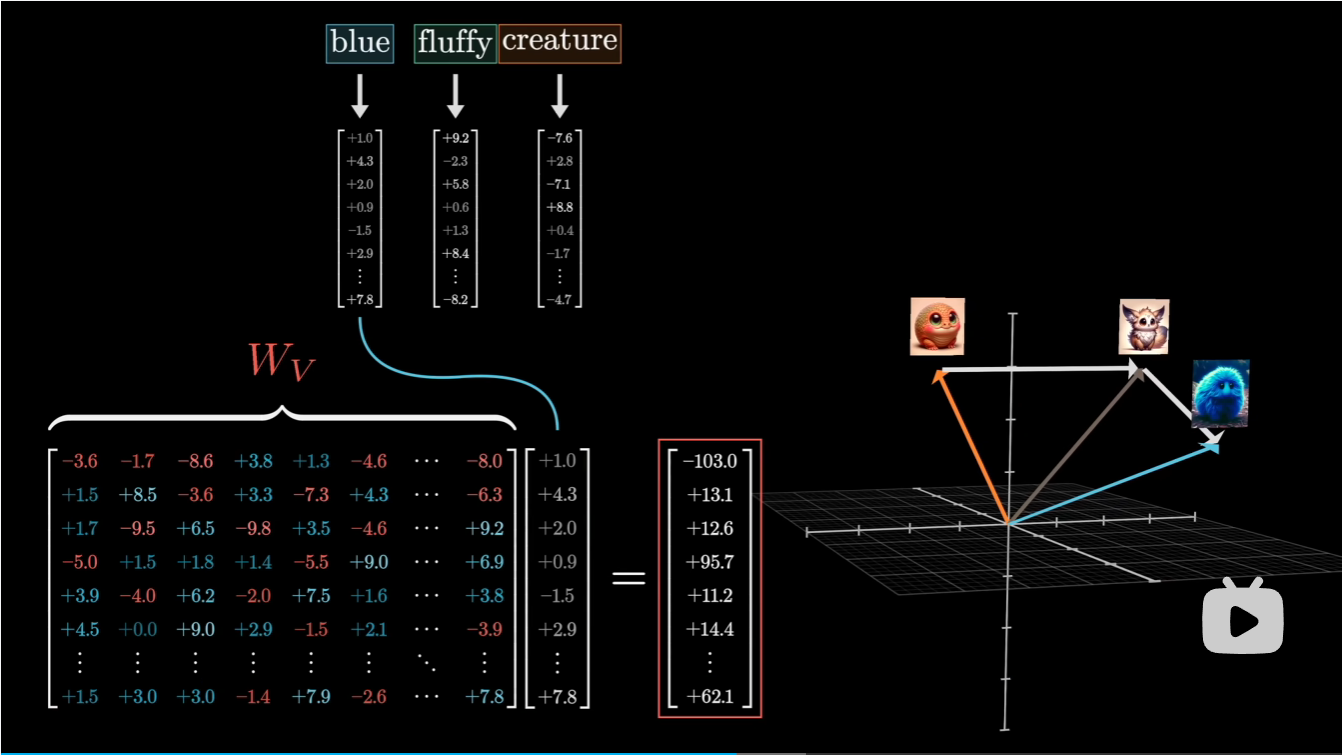
最后我们还有值矩阵\(W_V\), 与每个词向量\(\vec{E_i}\)相乘,得到\(\vec{V_i}\),然后每一个\(\vec{V_i}\)与上述的相关度表中的相关度进行点积:


值矩阵\(W_V\)是12288x12288的,即其行列大小都是词维度大小
通过上述步骤我们就完成了通过self-attention达到更新各个词向量的目的
实际中值矩阵会很大,我们一般会将值矩阵进行分解为两个小矩阵相乘:
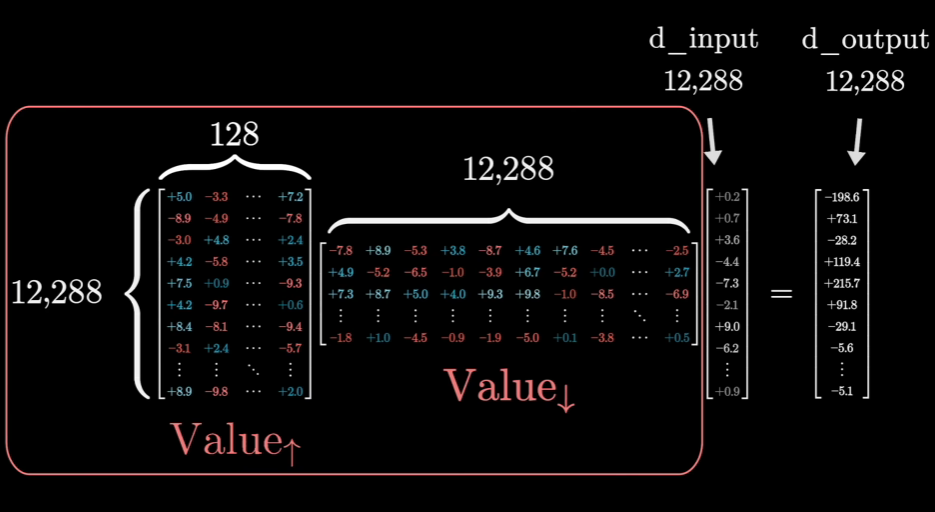
多头注意力
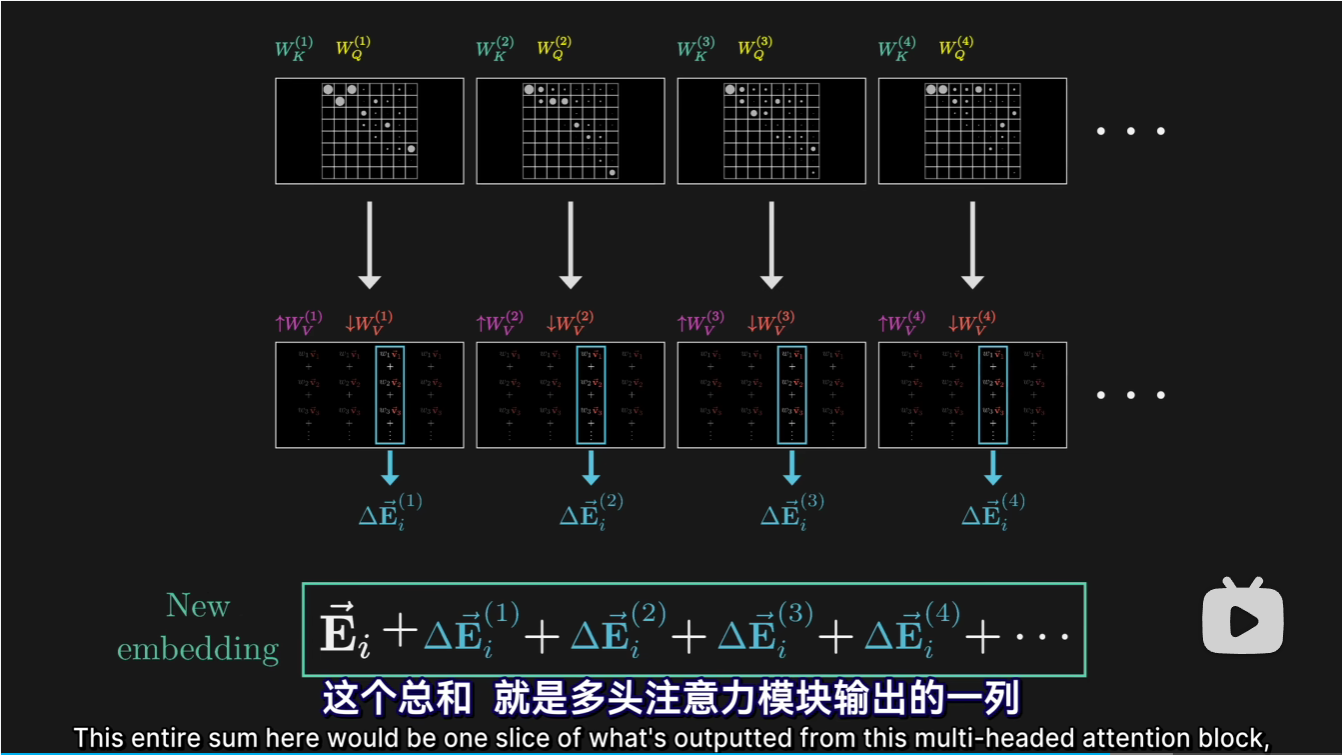
上述我们只有一个Attention模块,那么当有多个Attention模块呢?
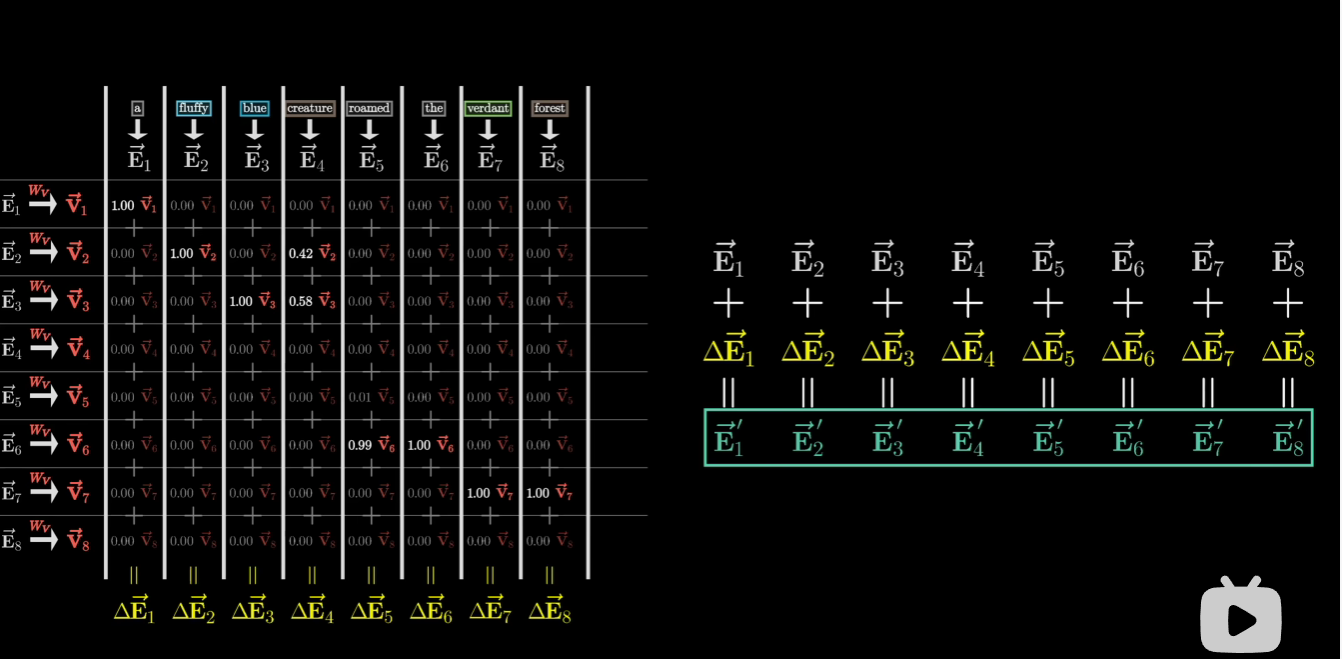
每一个Attention模块j会对每一个词向量\(\vec{E_i}\)得出\(\triangle {E_{i}^{j}}\)
最后我们只要将原始词向量累加上这些Attention模块给出变化量即可



 浙公网安备 33010602011771号
浙公网安备 33010602011771号