AtCoder Beginner Contest 277
《D - Takahashi's Solitaire》
思维,看题,循环

注意到Ai<M,这个意味着 最大的数 与 最小的数 之间可能会有循环,即一个排好的数(从小到大):
a1,a2,a3,.................,an-1,an; 可能(an+1)%m==a1;
(这道题的难点是强迫自己能1s跑出来)
经过推导我们不难发现:
一旦第一张牌确定了,那么结果也就出来了,我们将排序,去重后第i张牌第一次放的最终结果设为Si
将全部牌求和为all,排序,去重,记录第i张牌的数vi在原来数组中的出现次数为fi;
排序,去重后的数组大小为k
则有:
if (vi+1)%m != v[(i+1)%k]------->S[i]=all-vi*fi
if (vi+1)%m==v[(i+1)%k]--------->S[i]=S[i+1]-vi*fi;
有点dp递推的味道了,要选好一个方向来:即找到第一个(vi+1)%m != v[(i+1)%k]的牌p
即有0~p-1都是(vi+1)%m==v[(i+1)%k]
S[p]=all-vp*fp,S[0~p-1]=S[xxx]-vxxx*fxxx;
然后对于第k-1张牌来说,其上一张牌为0(因为那个%m),很自然我们会想到从k-1,k-2......p+1开始求
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <map>
using namespace std;
typedef long long ll;
const int N = 2 * 1e5 + 5;
map<ll, ll> mapp;
vector<ll> arr;
int main()
{
ll n, m;
ll all = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
int num;
scanf("%d", &num);
arr.push_back(num);
mapp[num]++;
all += num;
}
sort(arr.begin(), arr.end());
arr.erase(unique(arr.begin(), arr.end()), arr.end());
int k = arr.size();
// 找到最小的不连续的
int p;
for (int i = 0; i < k; i++)
{
if ((arr[i] + 1) % m != arr[(i + 1) % k])
{
p = i;
break;
}
}
ll ans = 1e16, s[N];
if (p == k - 1)
ans = 0;
else
{
// 极度要注意一下这里的乘法:会爆int,如果这里不转一下long long 或者 数据不是long long 的则会计算错误
s[p] = all - arr[p] * mapp[arr[p]];
for (int i = p - 1; i >= 0; i--)
s[i] = s[i + 1] - arr[i] * mapp[arr[i]];
for (int i = k - 1; i >= p + 1; i--)
{
if ((arr[i] + 1) % m == arr[(i + 1) % k])
s[i] = s[(i + 1) % k] - arr[i] * mapp[arr[i]];
else
s[i] = all - arr[i] * mapp[arr[i]];
}
for (int i = 0; i <= k - 1; i++)
ans = min(ans, s[i]);
}
cout << ans;
return 0;
}
《E - Crystal Switches》
分层图,图论,双端队列BFS
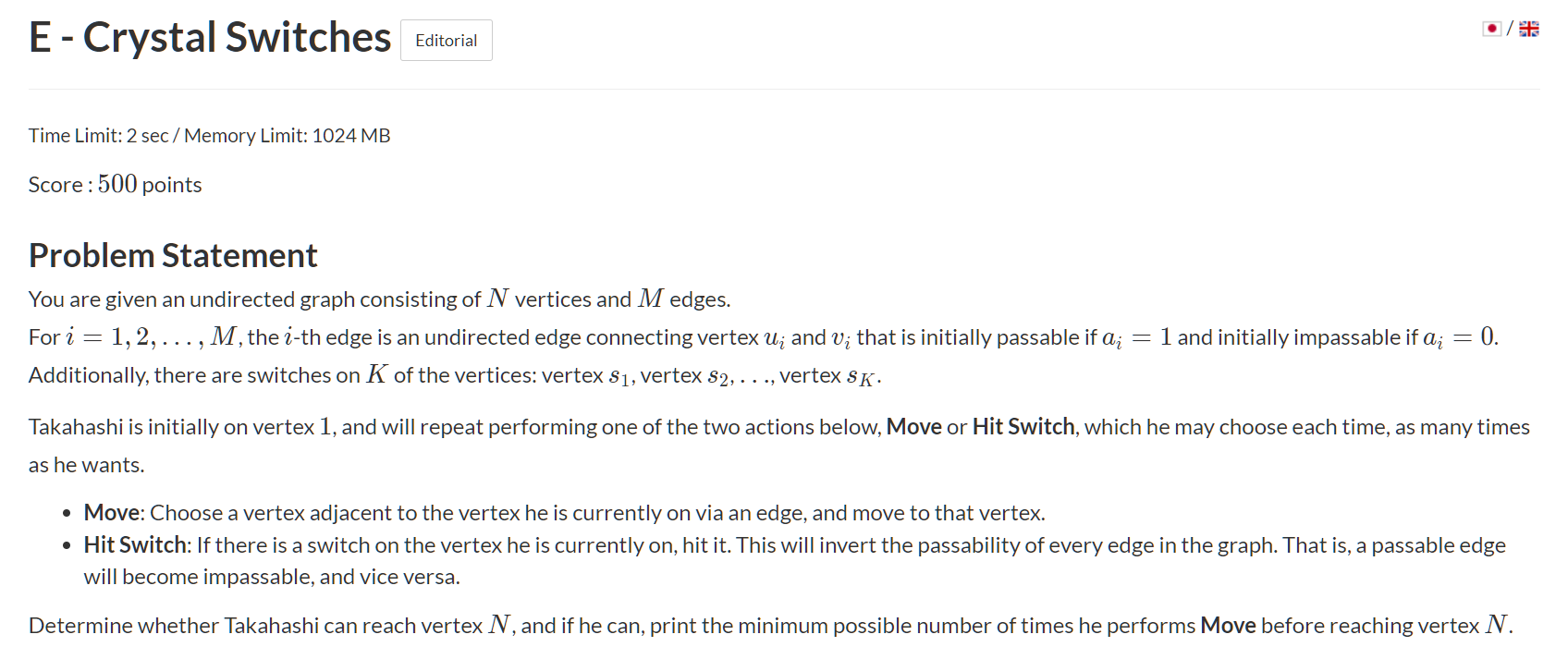
对于这道题:
可以看成每个点都是有两个状态;

正如样例:在最开始的情况下点1是不能直接到点3的,但是我们到点3处经过反转,点1就可以直接到点3了
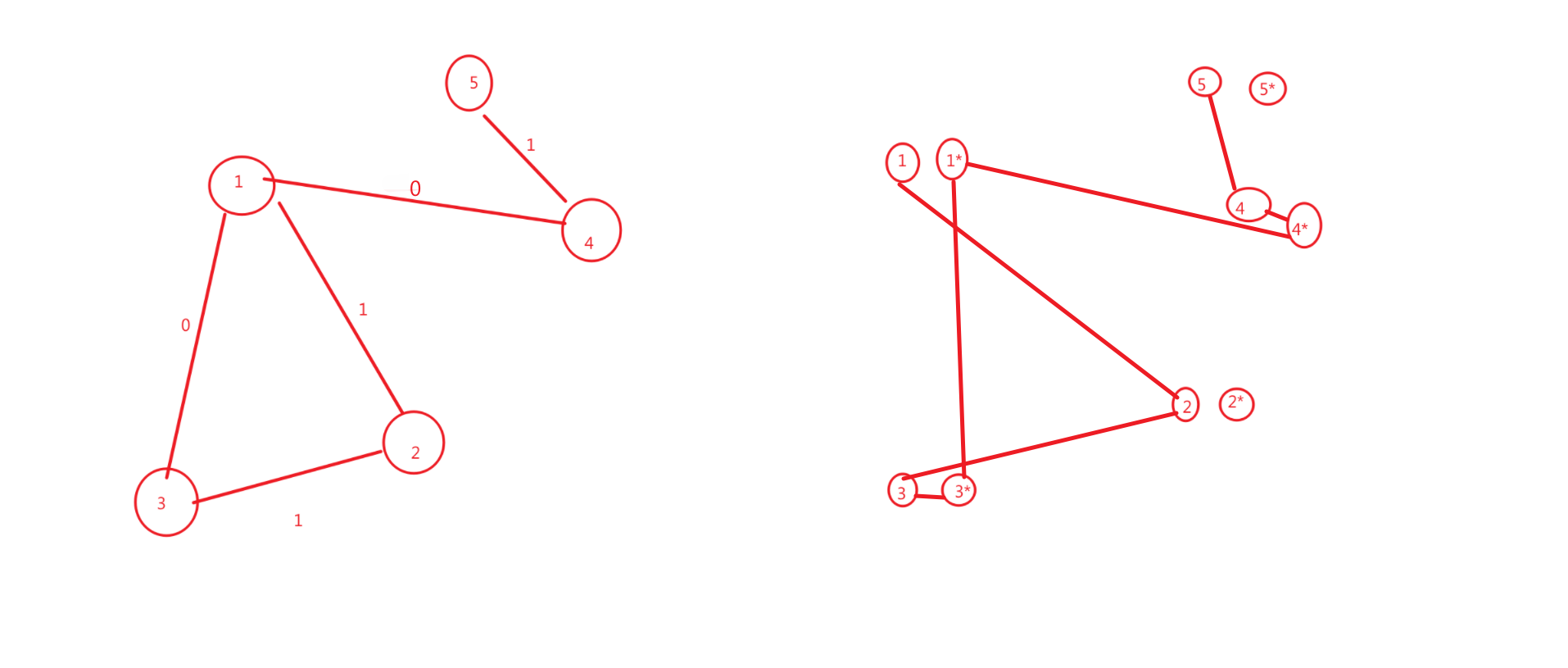
我们可以将 Hit Switch 操作看成一次不需要代价的状态转移,如图:
这个时候如果我们将图建成上面的样子,那么就可以直接用Dijkstra算法解决,但是在仔细思考一下,因为边的权重只有0与1,则也可以用双端BFS
那么问题来了:如何表示这同一个点,但是是不同状态下的?
可以对于点i,i+n表示其反状态
双端队列BFS的写法十分有讲解,不太熟悉尽量写Dijkstra
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <vector>
5 #include <deque>
6 using namespace std;
7 const int N = 4 * 1e5 + 5;
8 typedef pair<int, int> PII;
9 vector<PII> sides[N];
10 int n, m, k;
11 int dist[N];
12 bool vis[N];
13 void BFS()
14 {
15 memset(dist, 0x3f, sizeof(dist));
16 deque<int> dq;
17 dq.push_back(1);
18 dist[1] = 0;
19 while (dq.size())
20 {
21 int v = dq.front();
22 dq.pop_front();
23 // 避免TLE;
24 if (vis[v])
25 continue;
26 // 只有真正从队头出来的才是真正的到点v最短
27 vis[v] = true;
28 for (int i = 0; i < sides[v].size(); i++)
29 {
30 int to = sides[v][i].first, w = sides[v][i].second;
31 if (!vis[to] && dist[v] + w < dist[to])
32 {
33 dist[to] = dist[v] + w;
34 if (w == 0)
35 dq.push_front(to);
36 else
37 dq.push_back(to);
38 }
39 }
40 }
41 }
42 int main()
43 {
44 cin >> n >> m >> k;
45 for (int i = 1; i <= m; i++)
46 {
47 int a, b, s;
48 scanf("%d%d%d", &a, &b, &s);
49 if (s == 0)
50 sides[a + n].push_back({b + n, 1}), sides[b + n].push_back({a + n, 1});
51 else
52 sides[a].push_back({b, 1}), sides[b].push_back({a, 1});
53 }
54 for (int i = 1; i <= k; i++)
55 {
56 int v;
57 scanf("%d", &v);
58 sides[v].push_back({v + n, 0}), sides[v + n].push_back({v, 0});
59 }
60 BFS();
61 int ans = min(dist[n], dist[2 * n]);
62 if (ans == 0x3f3f3f3f)
63 ans = -1;
64 cout << ans;
65 return 0;
66 }
《F - Sorting a Matrix 》
思维,拓扑图
这个我看题解说道了偏序关系建图,这个我实在不会
但是这道题目的核心观点我大概理解了:

我们可以明确一个重点:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号