图论----最近公共祖先问题（LCA：Least Common Ancestors问题）

 

多年后重新回来总结一下倍增LCA的初始化，倍增数组等

　　首先我们需要初始化的是deep数组

　　memset(deep,0x3f,sizeof（deep))

　　初始化这个数组的目的是为了可以不用st[]数组，来判断是否看过某些点

　　

　　这里设倍增数组为h[N][25]

　　初始化 deep[root]=0，h[root][0]=0 ，deep[0]=-1;

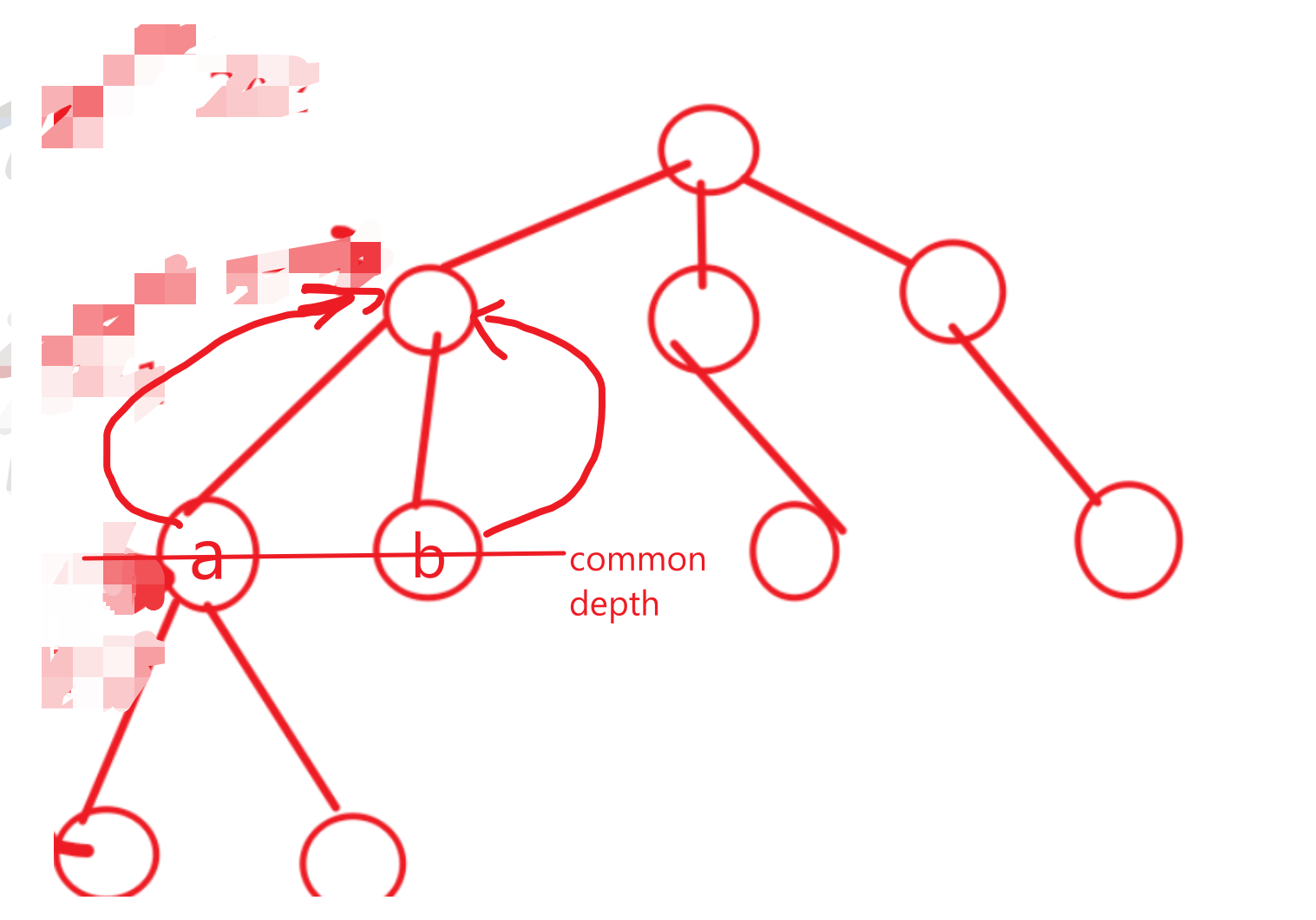
　　这里这样初始化的目的，如图：

 　　　　

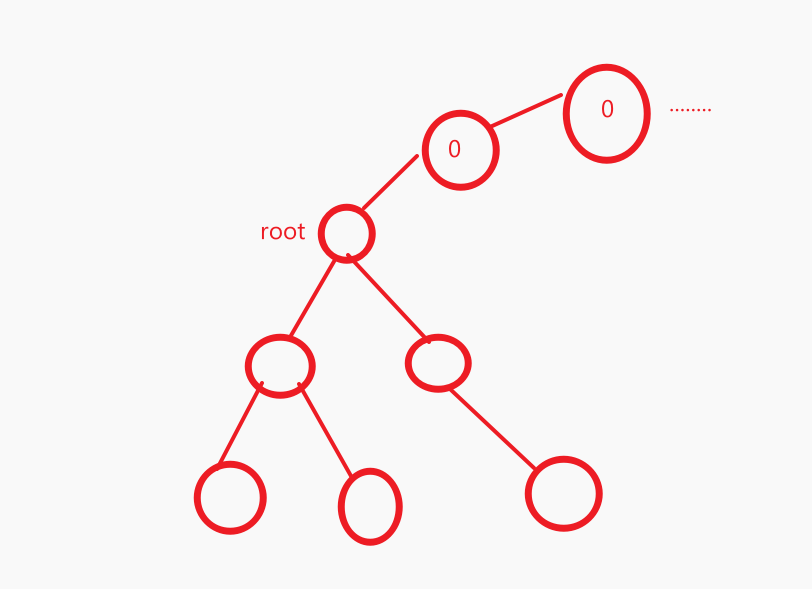
　　　　可以让超过root点的h[i][j]一直等于0

　　 含义即是i点跳2^j步后超过root点 所到达的点一直都是0

　　 然后设置deep[0]=-1,只要是为了下面LCA()函数中

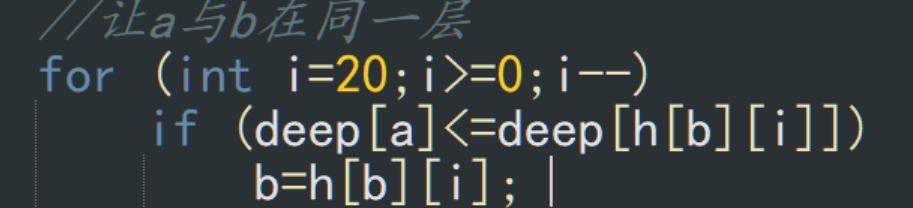
 这个判断中让b跳出了root点到0点不会被接受

 

 

 

 

 

 

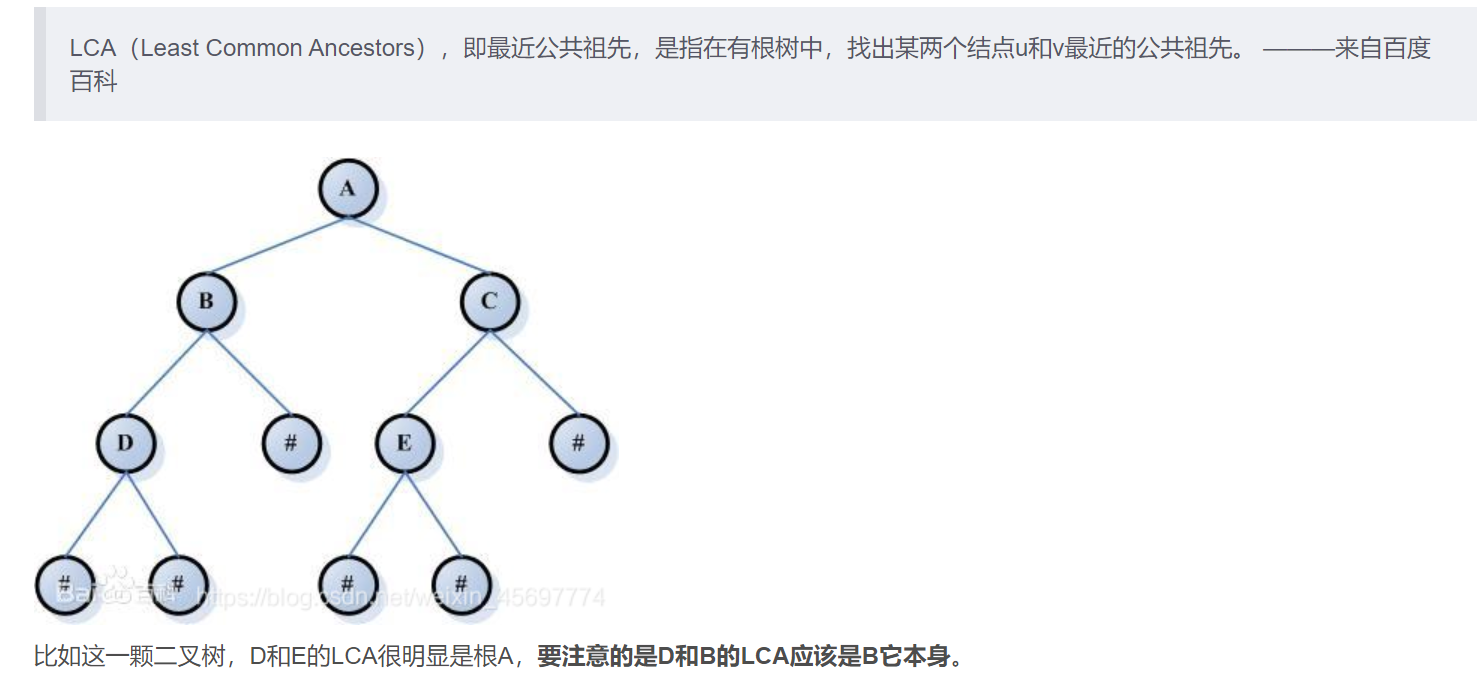
 注意到：在一棵树上的任意两个点之间一定都有公共祖先（最坏的情况下就是根节点了）

求两个点之间的最短距离其实就是求: 两个点到最近公共祖先的距离之和

那如何求最近公共祖先是谁呢？

　　1.首先我们定义一个函数lca(int a,int b),其作用是返回a,b两点的最近公共祖先

　　2.定义一个depth[]数组，代表每一个点在树中的深度； 规范　　depth[root]=1 

　　　定义一个f[N][logN+1]数组（N是节点总数），f[i][j]代表在点i处往上走2^j个点到达的点是f[i][j];

　　   规定 f[i][0]=i的父节点，跳出树的节点或根本不在树上的节点depth[]=0

 

 

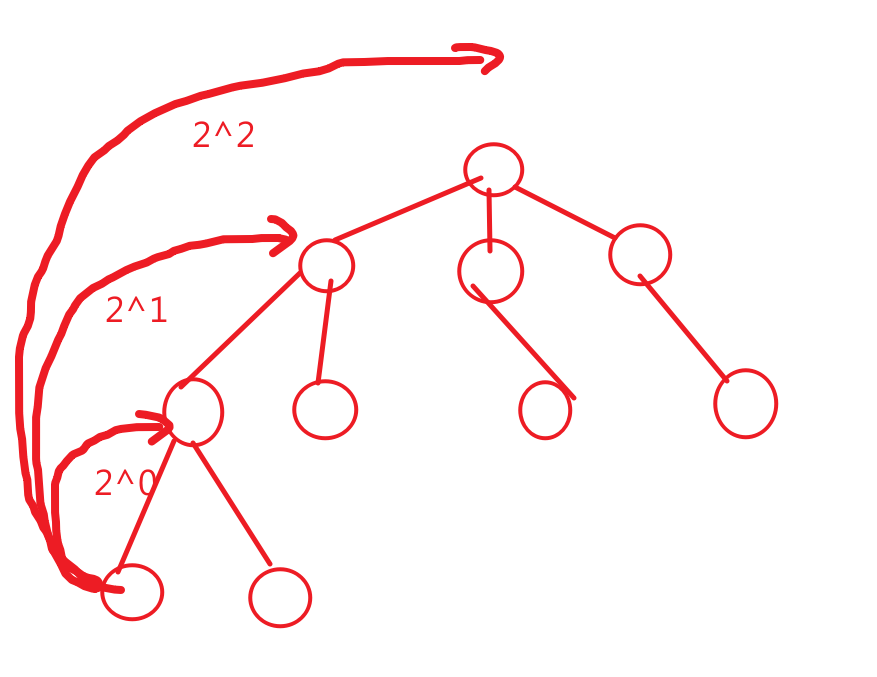
 lca函数具体做法：

　　首先，同过depth[],将两个点a，b跳到同一层(这里我们规定depth[a]<=depth[b],所以只要对a点进行操作即可)

　　　　　　如何跳呢？

　　　　　　因为我们有f[i][j]; 首先将a点跳到与b点相同深度我们并不知道要跳过几个点（假设要跳x个点），

　但是我们知道在a点跳2^0个点到达的深度是：depth[f[a][0]],其他以此类推

一个数，一定能够由2的倍数拼凑出来

那么x也一定能由2的倍数拼凑出来，我们可以枚举for (int i=logN;i>=0;i--) 表示跳2^i个点（i<=logN的原因是跳2^logN个点会超过树上的全部点）

if  depth[f[a][i]]<=depth[b]; 那么：a=f[a][i];

　　到了同一个深度后，将两个点一起跳枚举for (int i=logN;i>=0;i--) ，一直跳到最近公共祖先的下一个点

　　注意：如果两个点在同一层时已经是同一个点了，则直接返回，这时b点就是最近公共祖先

　　如何判断是跳到了最近公共祖先的下一个点？

即两个点是不同时，说明还未到最近公共祖先及上面的点

然后返回f[a][0]即为最近公共祖先

 

 

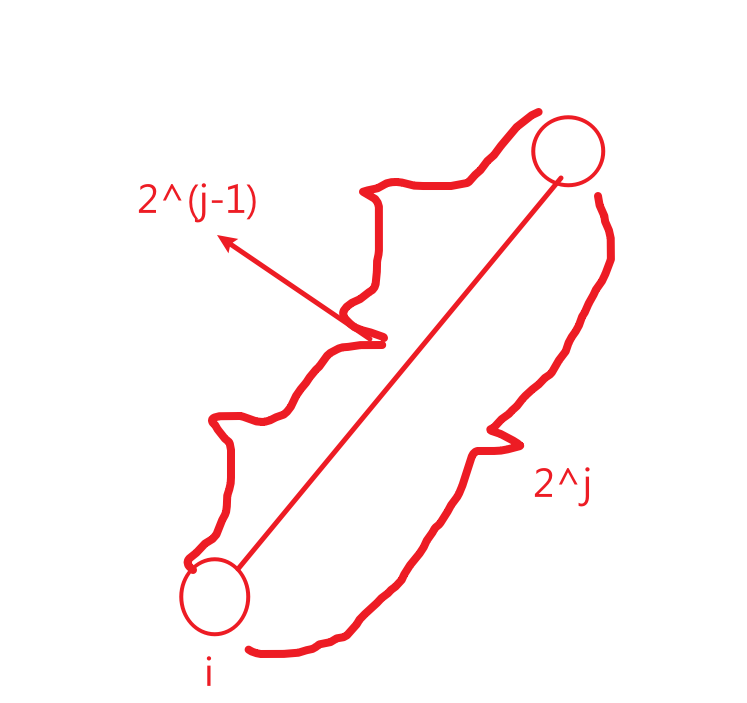
 　　如何求depth与f[i][j]?

　　f[i][j]=f【f【i】【j-1】】【j-1】;

 

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
// bfs时用的;
#include <queue>
//建树用的;
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 10010;
// fa[i][j]表示从点i开始出发跳2^j步能够到达的点为fa[i][j];
//由于0<logN<16(logN是以二为底的log),即跳2^16步会超过所以点数,
//最大跳2^15步,则j是从0~15,开数组开16位;
//哨兵:对于超过了树的点数的点为0;
int fa[N][14];
//记录一下每个点的深度，root的深度是1,哨兵(不存在的点，即跳出树的点)的深度为0,
int depth[N];
//记录每一个点到顶点的距离
int dist[N];
vector<PII> tree[N];
// bfs预处理fa,depth两个数组;
//预处理时间复杂度为O(nlogn);
//遍历到每一个点，对于每一个点循环logN次求出每一个点的fa[i][j]来
void bfs(int root)
{ //宽搜不容易因为递归层数过多爆栈
    memset(depth, 0x3f, sizeof(depth));
    memset(dist, 0, sizeof(dist));
    queue<int> q;
    depth[0] = 0, depth[root] = 1;
    q.push(root);
    while (q.size())
    {
        int t = q.front();
        q.pop();
        for (int i = 0; i < tree[t].size(); i++)
        {
            int child = tree[t][i].first;
            //注意:因为这里是有向树,则一定要除去已经看过的点
            if (depth[child] > depth[t] + 1)
            {
                q.push(child);
                //处理每一个点到顶点的距离:
                dist[child] = dist[t] + tree[t][i].second;
                //处理深度
                depth[child] = depth[t] + 1;
                //处理fa数组
                fa[child][0] = t;
                //这里15就是通过上面logN算出来的;
                // 0步上面已经处理过了
                for (int j = 1; j <= 13; j++)
                    fa[child][j] = fa[fa[child][j - 1]][j - 1];
            }
        }
    }
}
//一次询问的时间复杂度是O(logN);
int lca(int a, int b)
{
    if (depth[a] < depth[b])
        swap(a, b);
    // 1.首先让a点与b点处于同一层
    for (int k = 13; k >= 0; k--)
        if (depth[fa[a][k]] >= depth[b])
        {
            a = fa[a][k];
        }
    //让其同一层后:
    // 1.如果已经是同一个点了:
    if (a == b)
        return b;
    // 2.还不是同一个点,让a,b两点一起向上跳,直到到了最近公共祖先的下一层:
    //如何判断是最近公共祖先的下一层？
    //首先,两点肯定不相同:fa[a][k]!=fa[b][k];
    //其次在上面的情况下:fa[a][0]==fa[b][0],再移动一点就相同说明到达了最近公共祖先
    for (int k = 13; k >= 0; k--)
    {
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    }
    //因为树上任意两个点一定有公共祖先
    //经过上面的处理，一定两点到达了最近公共祖先的下一层;
    //返回两点的最近公共祖先;
    return fa[a][0];
}
int main()
{
    //默认root=1;
    int n, m, rd[N], root = 1;
    cin >> n >> m;
    for (int i = 1; i <= n - 1; i++)
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        tree[a].push_back({b, w});
        tree[b].push_back({a, w});
    }
    bfs(root);
    //开始处理读入:
    while (m--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        //树上任意两个点一定有公共祖先
        //函数lca的作用是返回点a,b的最近公共祖先;
        int node = lca(a, b);
        cout << dist[a] + dist[b] - dist[node] * 2 << endl;
    }
    return 0;
}

 《树剖求lca》

这里有几个数组是必要的,首先我们是通过top[]来判断是否在同一条链上

而要知道top[]，就要知道son[],要知道son[]就要知道sizer[]

像f[],dep[]数组更是必要的

更详细的树剖内容：https://www.cnblogs.com/cilinmengye/p/16607480.html

int sizer[N], f[N], dep[N], son[N];
void dfs1(int x, int from, int d)
{
    f[x] = from, dep[x] = d, sizer[x] = 1, son[x] = -1;
    for (int i = 0; i < tree[x].size(); i++)
    {
        int child = tree[x][i];
        if (child == from)
            continue;
        dfs1(child, x, d + 1);
        sizer[x] += sizer[child];
        if (son[x] == -1 || sizer[son[x]] < sizer[child])
            son[x] = child;
    }
}
// sum[i]表示点i到根节点的权值
int top[N];
void dfs2(int x, int from, int t)
{
    top[x] = t;
    if (son[x] != -1)
        dfs2(son[x], x, t);
    for (int i = 0; i < tree[x].size(); i++)
    {
        int child = tree[x][i];
        if (child == from || child == son[x])
            continue;
        dfs2(child, x, child);
    }
}
int lca(int a, int b)
{
    while (top[a] != top[b])
    {
        if (dep[top[a]] < dep[top[b]])
            swap(a, b);
        a = f[top[a]];
    }
    if (dep[a] > dep[b])
        swap(a, b);
    return a;
}