模二补码回绕

Two's Complement Wrap-Around

In this section, we give an example showing how temporary overflow in two's complement fixed-point causes no ill effects.

In 3-bit signed fixed-point arithmetic, the available numbers are as shown in Table 9.1.

 

 

Decimal	Binary
-4	100
-3	101
-2	110
-1	111
0	000
1	001
2	010
3	011

 

Let's perform the sum  , which gives a temporary overflow ( , which wraps around to  ), but a final result ( ) which is in the allowed range  :^10.3

 

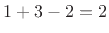
Now let's do  in three-bit two's complement:

 

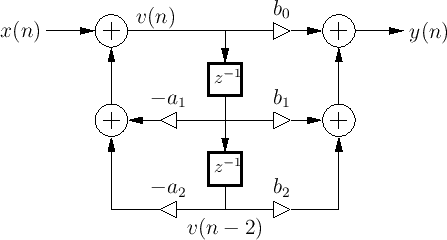
In both examples, the intermediate result overflows, but the final result is correct. Another way to state what happened is that a positive wrap-around in the first addition is canceled by a negative wrap-around in the second addition.

https://ccrma.stanford.edu/~jos/fp/Two_s_Complement_Wrap_Around.html

模二补码回绕
在本节中，我们给出了一个例子，说明模二补码定点数中的，临时溢出如何不会造成不良影响。
在3位有符号定点算术中，可用数字如表9.1所示。
表9.1：三位二补二进制定点数。
十进制　　二进制
-4 　　　　100
-3　　　　 101
-2　　　　 110
-1　　　　 111
0 　　　　000
1　　　　 001
2　　　　 010
3 　　　　011
让我们执行 3 + 3 - 4 =  2 的求和，这会产生一个临时溢出（3+3=6，为-2），但最终结果（2）在允许的范围内[-4,3]

011+011 = -110 （3+3=-2 （ {mod}  8  ） 
110+100 = 010     { （ -2 -4 =2  {mod} 8 ）}

现在让我们在三位二进制补码中做  1+3-2=2 ：
开始
001+011 =100 { （1+3=-4 ； t（ {mod} 8 } 
100+110&= 010 { （-4-2=2  mod  8 ） }
 
在这两个例子中，中间结果溢出，但最终结果是正确的。另一种表述发生了什么的方式是，第一次加法中的正向环绕被第二次加法中负向环绕所抵消。