189. 旋转数组

题目：
给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

进阶：

尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

提示：

1 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

方法一

方法一为使用额外的数组。我们将i位置的数放置到(i+k)%size上。放置完后，我们将额外的数组重新复制到nums上。为什么是(i+k)%size呢？我们参考学习数据结构时候学习的用数组实现的队列，(rear-front+QueueSize)%QueueSize。实际上，我们就是让数组位置跳跃的同时，不会照成数组越界，如果超过了size-1，那么插入到开头。

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        //思想类似于用数组实现的队列
        int size = nums.size();
        vector<int> ans(size);
        for(int i=0;i<size;i++){
            ans[(i+k)%size]=nums[i];
        }
        for(int i=0;i<size;i++){
            nums[i]=ans[i];
        }
    }
};

方法二：

置换法

n=7,k=2

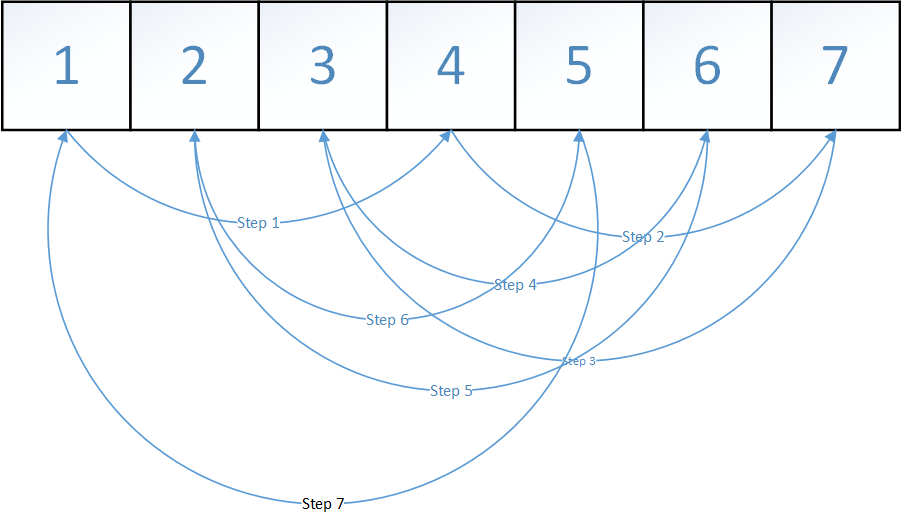
看到这道题，我想到了曾经离散数学学过的置换，用轮换表达式可以写成

\[\left( \begin{matrix} 1& 4& 7& 3& 6& 2& 5\\ 4& 7& 3& 6& 2& 5& 1\\ \end{matrix} \right) \]

这就是一组轮换，多次置换后回到原点。但是当n=6,k=2时

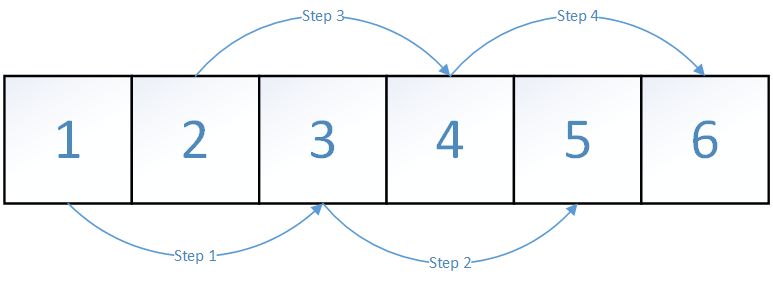
写成轮换表达式

\[\left( \begin{matrix} 1& 3& 5& 2& 4& 6\\ 3& 5& 1& 4& 6& 2\\ \end{matrix} \right) \]

实际上，对于第二种，我们进行两轮的轮换。
通过找规律，我们知道轮换的次数为n和k的最大公约数。

class Solution {
public:
    int gcd(int n,int k){
        int min;
        if(n<k)
            min = n;
        else
            min = k;
        int max=1;
        for(int i=1;i<=min;i++){
            if(n%i==0&&k%i==0&&i>max)
                max = i;
        }
        return max;
    }

    void rotate(vector<int>& nums, int k) {
        int size = nums.size();
        //计算最大公约数
        int count = gcd(size,k);
        for(int i=0;i<count;i++){
            int start = i;
            int end = (start+k)%size;
            while(end!=start){
                int temp;
                //交换位置
                temp = nums[start];
                nums[start]=nums[end];
                nums[end] = temp;
                end = (end+k)%size;
            }
        }
    }
};

方法三：

未反转	1 2 3 4 5 6 7
全部反转	7 6 5 4 3 2 1
反转(0,(k%size)-1)	6 7 5 4 3 2 1
反转((k%size),size1)	6 7 1 2 3 4 5

实际上操作步骤就是先将整个数组反转，然后在将数组分成两部分继续反转。

在程序中，我们直接调用algorithm里面的reverse函数来进行反转。

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        //反转数组法
        int size = nums.size();
        reverse(nums.begin(),nums.end());
        reverse(nums.begin(),nums.begin()+(k%size));
        reverse(nums.begin()+(k%size),nums.end());
    }
};