动态规划算法

动态规划算法使用场景

　　在学习和工作中，我们常常会听说某类问题的解决使用动态规划算法，可以快速高效的得出答案，但是很多人可能和我一样，并没有一个很明确的概念可以清楚的知道动态规划问题是用来求解哪一类问题的。

　　首先我们来看一下维基百科对动态规划的解释： 

　　动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

　　简单来说，动态规划是用来解决可拆分问题的，一个问题的解，是由其多个子解构成，且多个子解有重复，我们一直对问题进行拆分，直到子问题可以直接解决。在求解的过程中，把求解过的问题子解保存，以减少重复计算，再根据子问题解反推出该问题解的一种手段。

　　这么说可能还是有点绕，不过记住，动态规划的核心思想有以下三点： 

• 递归的去拆分问题为子问题，知道子问题可以直接求解
• 记住求解过的子问题
• 因为求过的子问题有记录，减少重复计算

一个例子帮助理解动态规划

　　求解斐波那契数列的第n项值。

　　我们都知道斐波那契数列第n项的值等于其前两项的和，根据其特性，我们可以写出斐波那契数列第n项的 状态转移方程

 

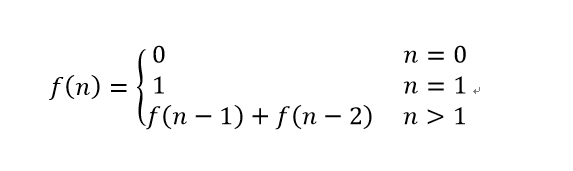
 　　使用反推法，要求f(n), 即要求出 f(n-1) 和 f(n-2), 直到推算到斐波那契数列的前两个项，即子解确定。

                

 

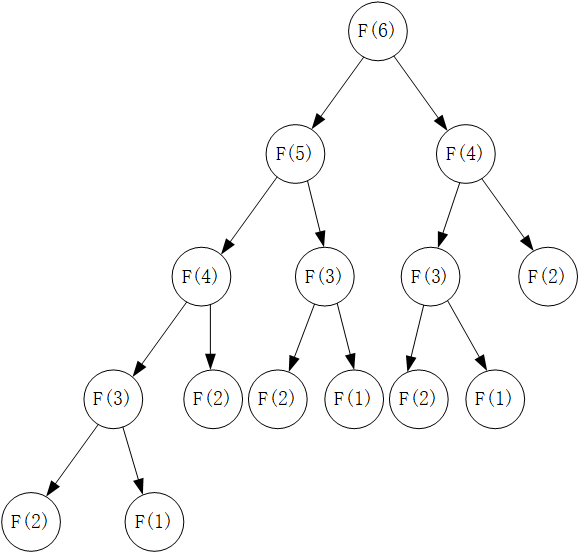
　　我们可以发现，在求解的过程中，有很多的重复解，我们可以把这些解保存下来，后面求其他解时直接使用，降低算法复杂度。

　　在实际求解过程中，子解的用途是有规律的，我们只用到当前解的前两个解，所以只用保存当前解的前两个解即可。

　　代码如下：

int GetFiboN(int n)
{
    int Fa = 0;
    int Fb = 1;
    int Fn = 0;
    int i = 0;
    if(n < 1) //项不能小于1
        return -1；
    if(n==1)
        return Fa;       
    if(n==2)
        return Fb;     
    for(i=3;  i<=n; i++)
    {
        Fn=Fa+Fb;
        Fa=Fb;
        Fb=Fn;
    }
    return Fn;
}