软光栅从零开始——透视矫正

推导

• 为什么需要透视矫正(Perspective-Correct Interpolation)？

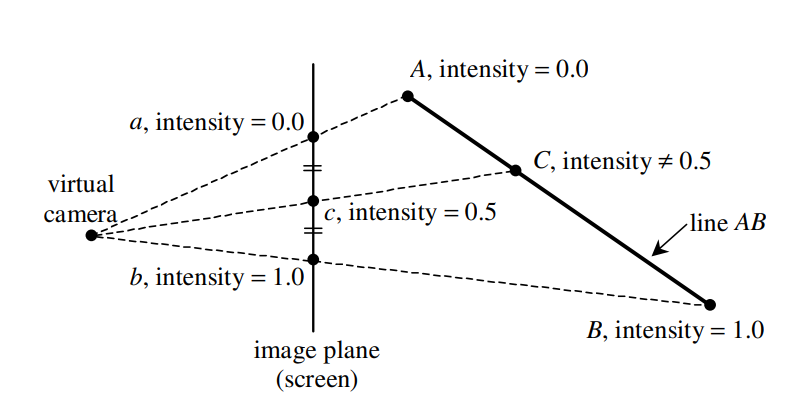
  在Phong Shading中，我们提到过通过使用重心插值的方式求三角形内任意一点，但这个重心插值的对象本应是世界空间中的坐标，但大多数计算都是使用透视投影后的二维平面内的数据,而恰恰问题就出在这里。如下图所示，在屏幕空间进行插值后得到c的intensity为0.5，但在观察空间中，点c的intensity不为0.5，也就是说透视投影后进行插值的坐标或属性会存在一定误差
  

• 如何进行矫正？

  为了证明更简洁，在此处我们采用深度值z的插值且只考虑x，z轴来介绍

  如下图所示，我们定义屏幕空间的插值比例为s,而观察空间的比例为t,坐标\(a(u_1,d),c(u_s,d),b(u_2,d),A(X_1,Z_1),C(X_t,Z_t),B(X_2,Z_2)\)
  

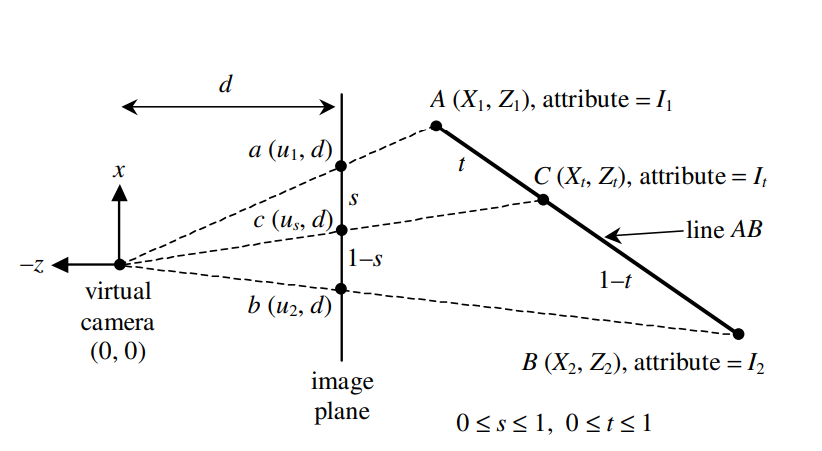
  推导过程如下：

  根据上图可以轻易得到以下三个式子:

  1. \(\begin{equation} \frac{X_1}{Z_1} = \frac{u_1}{d} \Rightarrow X_1 = \frac{u_1 Z_1}{d} \tag{1} \end{equation}\)
  2. \(\begin{equation} \frac{X_2}{Z_2} = \frac{u_2}{d} \Rightarrow X_2 = \frac{u_2 Z_2}{d} \tag{2} \end{equation}\)
  3. \(\begin{equation} \frac{X_t}{Z_t} = \frac{u_s}{d} \Rightarrow Z_t = \frac{d X_t}{u_s} \tag{3} \end{equation}\)

  对观察空间和屏幕空间进行插值，可以得到如下三个式子:

  1. \(\begin{equation} u_s = u_1 + s(u_2 - u_1) \tag{4} \end{equation}\)
  2. \(\begin{equation} X_t = X_1 + t(X_2 - X_1) \tag{5} \end{equation}\)
  3. \(\begin{equation} Z_t = Z_1 + t(Z_2 - Z_1) \tag{6} \end{equation}\)

  将式子(4)和(5)带入(3)，可得:

  \(\begin{equation} Z_t = \frac{d(X_1 + t(X_2 - X_1))}{u_1 + s(u_2 - u_1)} \tag{7} \end{equation}\)

  将式子(1)和(2)带入(7)，可得:

  \(\begin{equation} Z_t = \frac{d(\frac{u1 Z_1}{d} + t(\frac{u_2 Z_2}{d} - \frac{u_1 Z_1}{d}))}{u_1 + s(u_2 - u_1)} = \frac{u_1 Z_1 + t(u_2Z_2 - u_1 Z_1)}{u_1 + s(u_2 - u_1)} \tag{8} \end{equation}\)

  将式子(6)带入(8)，可得：

  \(\begin{equation} Z_1 + t(Z_2 - Z_1) = \frac{u_1 Z_1 + t(u_2 Z_2 - u_1 Z_1)}{u_1 + s(u_2 - u_1)} \tag{9} \end{equation}\)

  观察式子(9)可以得知，已经成功求得一个t和s的关系式，化简可得:

  \(\begin{equation} t = \frac{s Z_1}{s Z_1 + (1-s)Z_2} \tag{10} \end{equation}\)

  将式子(10)带入(6)，可得:

  \(\begin{equation} Z_t = Z_1 + \frac{s Z_1}{s Z_1 + (1-s)Z_2}(Z_2 - Z_1) \tag{11} \end{equation}\)

  对式子(11)化简，可得最终答案：

  \(\begin{equation} Z_t = \frac{1}{\frac{1}{Z_1} + s(\frac{1}{Z_2} - \frac{1}{Z_1})} \tag{12} \end{equation}\)

  虽然以上证明是线性插值的矫正过程，但对于重心坐标插值也同样适用。此处不再对其进行推导，直接给出公式。重心坐标插值的透视矫正公式：

  \(\begin{equation} Z_t = \frac{1}{\frac{\alpha}{Z_A} + \frac{\beta}{Z_B} + \frac{\gamma}{Z_C}} \tag{13} \end{equation}\)

• 推广，任意属性(法向量等)的插值结果

  推导如下：

  设任意属性为I

  易得：

  \(\begin{equation} I_t = I_1 + t(I_2 - I_1) \tag{14} \end{equation}\)

  将式子(10)带入(14)，可得：

  \(\begin{equation} I_t = I_1 + \frac{s Z_1}{s Z_1 + (1-s)Z_2}(I_2 - I_1) \tag{15} \end{equation}\)

  再排列一下：

  \(\begin{equation} I_t = \frac{(\frac{I_1}{Z_1} + s(\frac{I_2}{Z_2} - \frac{I_1}{Z_1}))}{(\frac{1}{Z_1} + s(\frac{1}{Z_2} - \frac{1}{Z_1}))} \tag{16} \end{equation}\)

  将式子(12)带入(16)，可得：

  \(\begin{equation} I_t = \frac{(\frac{I_1}{Z_1} + s(\frac{I_2}{Z_2} - \frac{I_1}{Z_1}))}{\frac{1}{Z_t}} \tag{17} \end{equation}\)

  类似，推出重心坐标插值的任意属性公式：

  \(\begin{equation} I_t = \frac{I_A\frac{\alpha}{Z_A} + I_B \frac{\beta}{Z_B} + I_c \frac{\gamma}{Z_C}}{\frac{1}{Z_t}} \tag{18} \end{equation}\)

  reference

  https://www.comp.nus.edu.sg/~lowkl/publications/lowk_persp_interp_techrep.pdf
  https://zhuanlan.zhihu.com/p/144331875