day12 简单神经网络学习

简单神经网络
tf.placeholder
Softmax函数和交叉熵
- 前提
- 实例
tf.nn.softmax_cross_entropy_with_logits
注：

简单神经网络

概念

代码

import numpy as np
import tensorflow.compat.v1 as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
tf.compat.v1.disable_eager_execution()
tf.disable_v2_behavior()
#加载数据集
mnist      = input_data.read_data_sets("C:/Users/chenqi/Desktop/data/mnist", one_hot=True)
# NETWORK TOPOLOGIES
n_hidden_1 = 256 
n_hidden_2 = 128 
n_input    = 784 
n_classes  = 10  

# 占位符
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
    
# NETWORK PARAMETERS
stddev = 0.1
weights = {
    'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1], stddev=stddev)),
    'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2], stddev=stddev)),
    'out': tf.Variable(tf.random_normal([n_hidden_2, n_classes], stddev=stddev))
}
biases = {
    'b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'out': tf.Variable(tf.random_normal([n_classes]))
}
print ("NETWORK READY")
def multilayer_perceptron(_X, _weights, _biases):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(_X, _weights['w1']), _biases['b1'])) 
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, _weights['w2']), _biases['b2']))
    return (tf.matmul(layer_2, _weights['out']) + _biases['out'])
# PREDICTION
pred = multilayer_perceptron(x, weights, biases)

# LOSS AND OPTIMIZER
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y)) 
optm = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) 
corr = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))    
accr = tf.reduce_mean(tf.cast(corr, "float"))

# INITIALIZER
init = tf.global_variables_initializer()
print ("FUNCTIONS READY")
training_epochs = 50
batch_size      = 100
display_step    = 5
# LAUNCH THE GRAPH
sess = tf.Session()
sess.run(init)
# OPTIMIZE
for epoch in range(training_epochs):
    avg_cost = 0.
    total_batch = int(mnist.train.num_examples/batch_size)
    # ITERATION
    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        feeds = {x: batch_xs, y: batch_ys}
        sess.run(optm, feed_dict=feeds)
        avg_cost += sess.run(cost, feed_dict=feeds)
    avg_cost = avg_cost / total_batch
    # DISPLAY
    if (epoch+1) % display_step == 0:
        print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
        feeds = {x: batch_xs, y: batch_ys}
        train_acc = sess.run(accr, feed_dict=feeds)
        print ("TRAIN ACCURACY: %.3f" % (train_acc))
        feeds = {x: mnist.test.images, y: mnist.test.labels}
        test_acc = sess.run(accr, feed_dict=feeds)
        print ("TEST ACCURACY: %.3f" % (test_acc))
print ("OPTIMIZATION FINISHED")

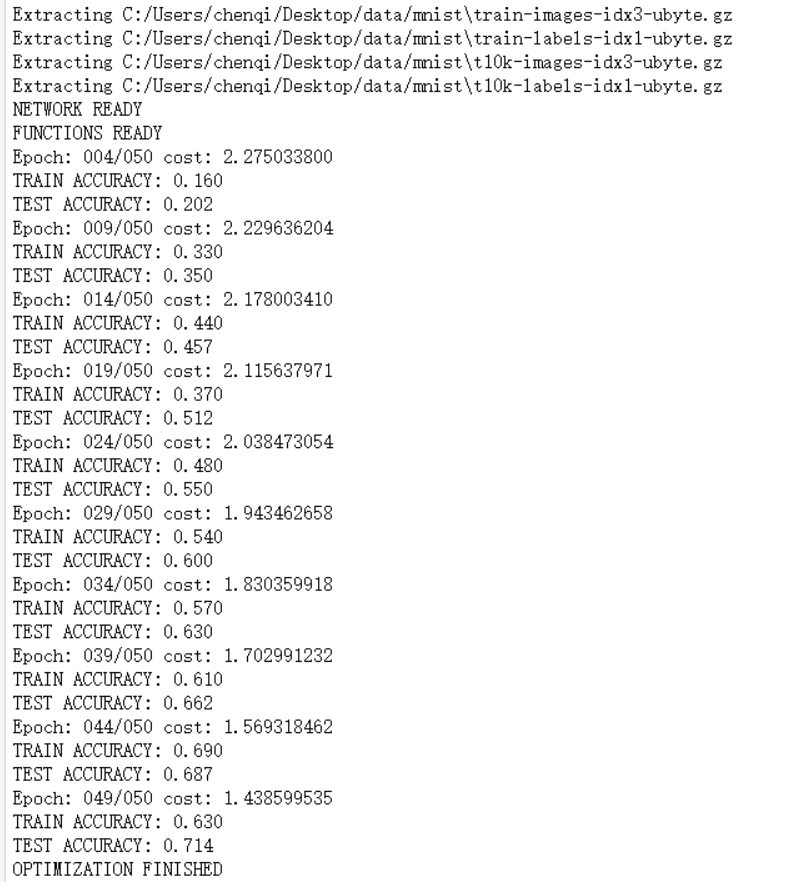
运行截图

tf.placeholder

代码

tf.placeholder(dtype, shape=None, name=None)

功能

此函数可以理解为形参，用于定义过程，在执行的时候再赋具体的值

参数

dtype：数据类型。常用的是tf.float32,tf.float64等数值类型
shape：数据形状。默认是None，就是一维值，也可以是多维，比如[2,3], [None, 3]表示列是3，行不定
name：名称。

Softmax函数和交叉熵

前提

前面逻辑回归中小提了softmax函数和交叉熵函数的概念。

在手写数字识别中，通过单层神经元产生连续的输出值y，将y再输入到softmax层处理，经过函数计算将结果映射为0~9每个数字对应的概率，概率越大表示该图片越像某个数字，所有数字的概率之和为1
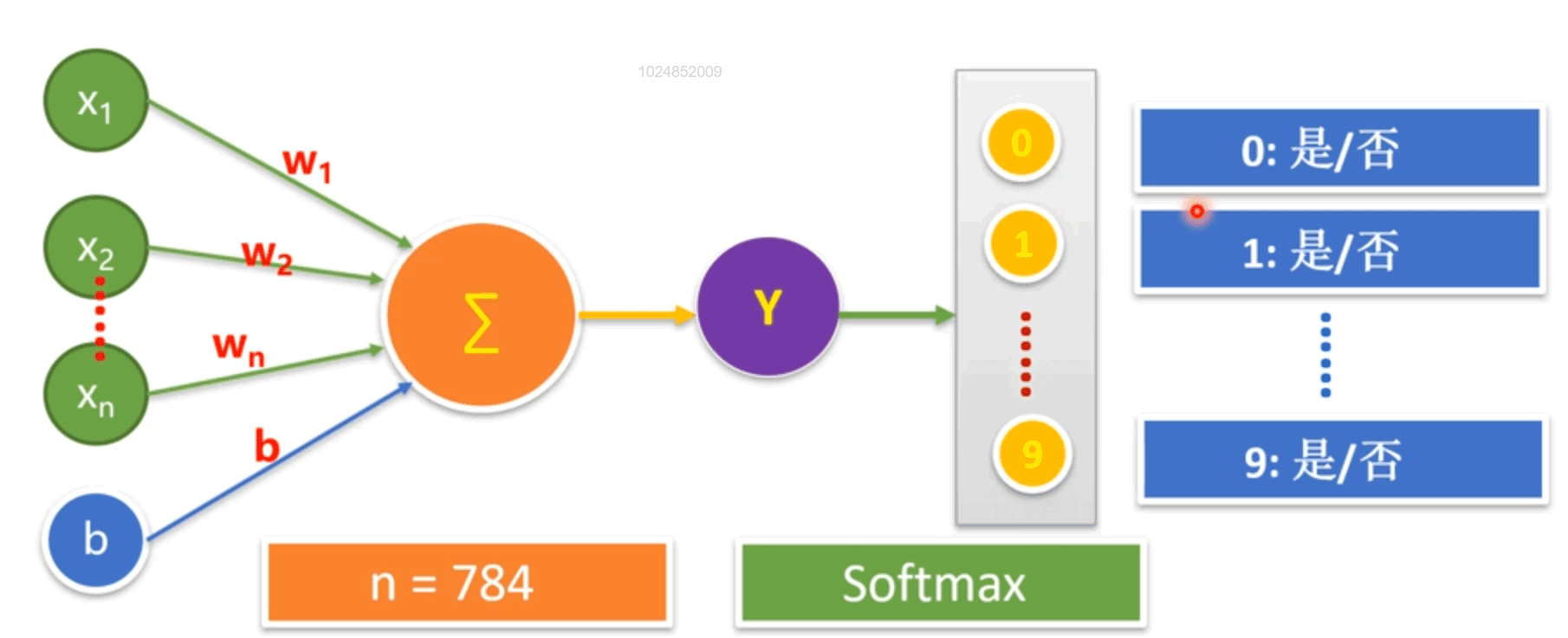
交叉熵损失函数：交叉熵用于刻画两个概率分布之间的距离，其中p代表正确答案，q代表预测值，交叉熵越小距离越近，从而模型的预测越准确。例如正确答案为(1,0,0)，甲模型预测为(0.5,0.2,0.3)，其交叉熵=-1log0.5≈0.3，乙模型(0.7,0.1,0.2)，其交叉熵=-1log0.7≈0.15，所以乙模型预测更准确

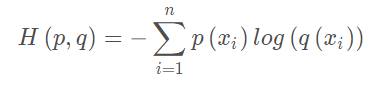
实例

这里会运用前面的逻辑回归实例代码和这次的简单神经网络实例代码来展示两种形式不同但是都是利用softmax和交叉熵损失函数的方法。

逻辑回归中

#将线性的输出y通过softmax转换0~9每个数字对应的概率
actv = tf.nn.softmax(tf.matmul(x, W) + b) 
#累加交叉熵代价函数-y*tf.log(pred)再对数据总量求均值
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(actv), reduction_indices=1))

简单神经网络中

#n_hidden_1=256、n_hidden_2=128、n_input=784、n_classes=10 
weights = {
    'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1], stddev=stddev)),
    'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2], stddev=stddev)),
    'out': tf.Variable(tf.random_normal([n_hidden_2, n_classes], stddev=stddev))
}
biases = {
    'b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'out': tf.Variable(tf.random_normal([n_classes]))
}
print ("NETWORK READY")
def multilayer_perceptron(_X, _weights, _biases):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(_X, _weights['w1']), _biases['b1'])) 
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, _weights['w2']), _biases['b2']))
    return (tf.matmul(layer_2, _weights['out']) + _biases['out'])

#这里没直接运用softmax函数来将线性的输出y通过softmax转换0~9每个数字对应的概率
#而是通过设置权重时多加了一个out和tf.matmul(layer_2, _weights['out']) + _biases['out']把最后的输出转换一个10分类的得分值（一个1行10列的向量）
pred = multilayer_perceptron(x, weights, biases)

#这里直接用tf.nn.softmax_cross_entropy_with_logits求交叉熵损失函数
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))

所以说其实两者是同一个道理，举例说明

import numpy as np
import tensorflow.compat.v1 as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
tf.compat.v1.disable_eager_execution()
tf.disable_v2_behavior()
#true label  
y_=tf.constant([[0.0,0.0,1.0],[0.0,0.0,1.0],[0.0,0.0,1.0]])  
#our NN's output  out层
logits=tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]])  

#第一种方法
#step1:do softmax  
y=tf.nn.softmax(logits)  
#step2:do cross_entropy  
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_*tf.log(y), reduction_indices=1))

#第二种方法
#do cross_entropy just one step  只需一步
cross_entropy2=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_)) 
  
with tf.Session() as sess:  
    softmax=sess.run(y)  
    c_e = sess.run(cross_entropy)  
    c_e2 = sess.run(cross_entropy2)  
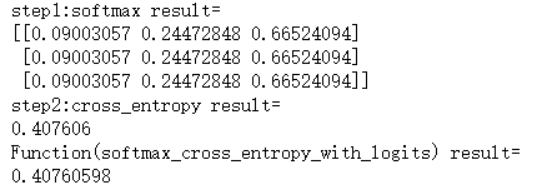
    print("step1:softmax result=")  
    print(softmax)  
    print("step2:cross_entropy result=")  
    print(c_e)  
    print("Function(softmax_cross_entropy_with_logits) result=")  
    print(c_e2)

tf.nn.softmax_cross_entropy_with_logits

代码

tf.nn.softmax_cross_entropy_with_logits(
    _sentinel=None,
    labels=None,
    logits=None,
    dim=-1,
    name=None
)

功能

这个函数的功能就是计算labels和logits之间的交叉熵（cross entropy）。

参数和原理

第一个参数基本不用。此处不说明。
第二个参数label的含义就是一个分类标签，所不同的是，这个label是分类的概率，比如说[0.2,0.3,0.5]，labels的每一行必须是一个概率分布（即概率之合加起来为1）也就是实际值。

现在来说明第三个参数logits，logit的值域范围[-inf,+inf]（即正负无穷区间）。我们可以把logist理解为原生态的、未经缩放的，可视为一种未归一化的“概率替代物”，如[4, 1, -2]。它可以是其他分类器（如逻辑回归等、SVM等）的输出。

例如，上述向量中“4”的值最大，因此，属于第1类的概率最大，“1”的值次之，所以属于第2类的概率次之。

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。

由于logis本身并不是一个概率，所以我们需要把logist的值变化成“概率模样”。这时Softmax函数该出场了。Softmax把一个系列的概率替代物（logits）从[-inf, +inf] 映射到[0,1]。除此之外，Softmax还保证把所有参与映射的值累计之和等于1，变成诸如[0.95, 0.05, 0]的概率向量。这样一来，经过Softmax加工的数据可以当做概率来用（如图2所示）。

经过softmax的加工，就变成“归一化”的概率（设为p1），这个新生成的概率p1，和labels所代表的概率分布（设为p2）一起作为参数，用来计算交叉熵。

这个差异信息，作为我们网络调参的依据，理想情况下，这两个分布尽量趋近最好。如果有差异（也可以理解为误差信号），我们就调整参数，让其变得更小，这就是损失（误差）函数的作用。

最终通过不断地调参，logit被锁定在一个最佳值（所谓最佳，是指让交叉熵最小，此时的网络参数也是最优的）。softmax和交叉熵的工作流程如图所示

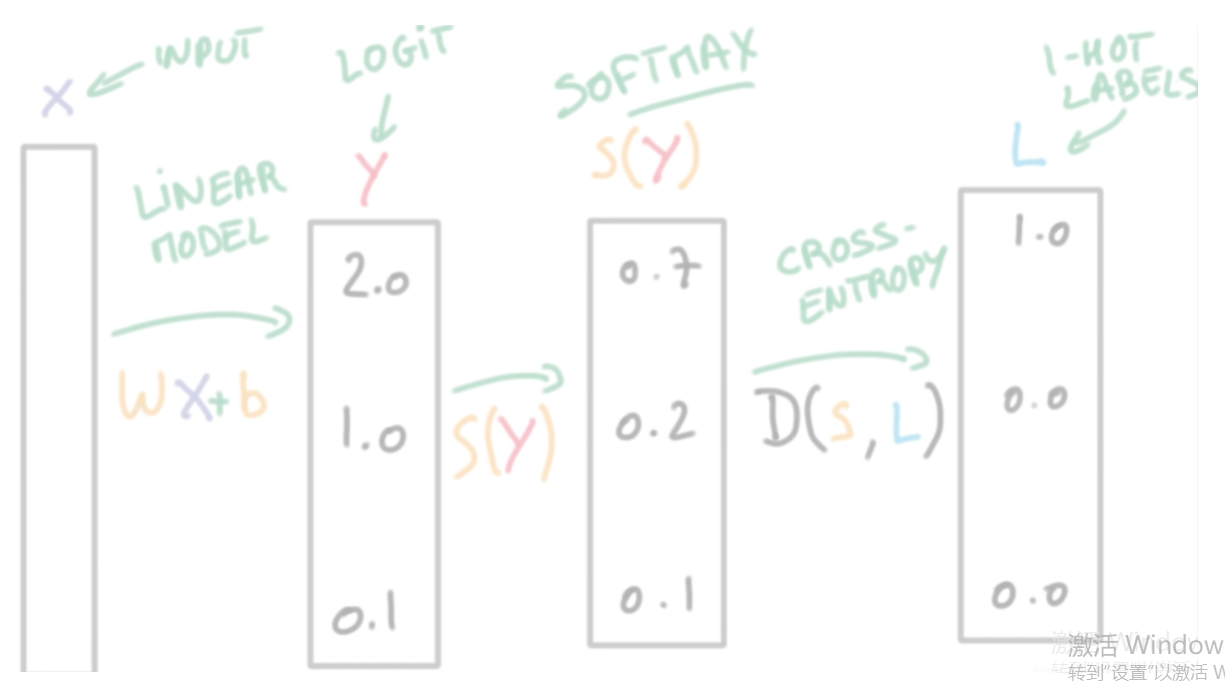
如果labels的每一行是one-hot表示，也就是只有一个地方为1（或者说100%），其他地方为0（或者说0%），还可以使用tf.sparse_softmax_cross_entropy_with_logits()。之所以用100%和0%描述，就是让它看起来像一个概率分布。
tf.nn.softmax_cross_entropy_with_logits函数已经过时 (deprecated)，它在TensorFlow未来的版本中将被去除。取而代之的是 tf.nn.softmax_cross_entropy_with_logits_v2。
参数labels,logits必须有相同的形状 [batch_size, num_classes] 和相同的类型(float16, float32, float64)中的一种，否则交叉熵无法计算。
tf.nn.softmax_cross_entropy_with_logits 函数内部的 logits 不能进行缩放，因为在这个工作会在该函数内部进行（注意函数名称中的 softmax ，它负责完成原始数据的归一化），如果 logits 进行了缩放，那么反而会影响计算正确性。

注：

本博客部分参考https://blog.csdn.net/yhily2008/article/details/80262321

和https://blog.csdn.net/zj360202/article/details/78582895

posted @ 2021-01-17 11:21 晨起阅读(74) 评论(0) 收藏举报

刷新页面返回顶部

woaiiu