Chi-square

卡方分布

，是为了解决衡量categorical data,尤其是nominal variables而创造出来的方法

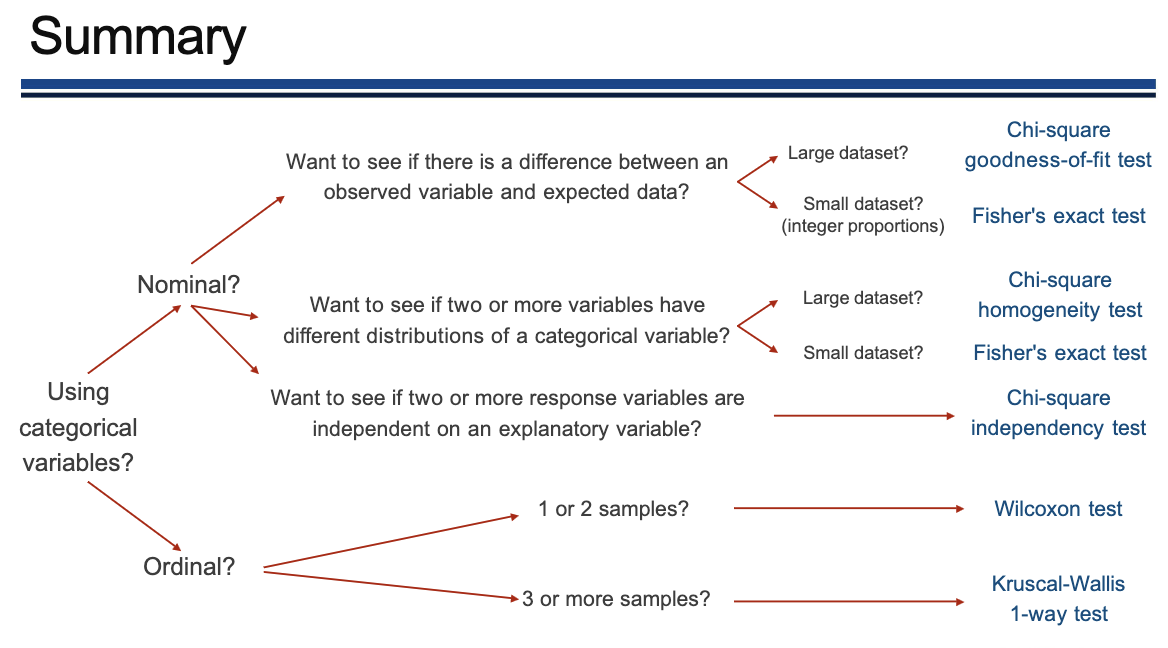
如果你的研究目的是比较实际观测值与某个理论分布或期望值，使用适合性检验。
如果你在比较两个或多个独立样本的分类变量分布是否有差异，使用同质性检验。
如果你在分析两个分类变量之间是否存在关联，使用独立性检验。

这三个检验类型——适合性检验、同质性检验和独立性检验——都是统计分析中用于检验不同假设的方法，但它们检验的目的和应用场景各不相同。下面我会详细解释它们的区别：

1. 适合性检验（Goodness-of-fit test）：

   • 目的：检验实际观测值是否与某个理论分布或期望值相符合。
   • 应用场景：当你有一个理论模型或分布，想要检验实际数据是否遵循这个模型或分布时使用。例如，检验抛硬币实验的结果是否符合理论上的50%正面和50%反面的概率分布。
   • 常用方法：卡方适合性检验（Chi-squared goodness-of-fit test）是常用的适合性检验方法。

2. 同质性检验（Homogeneity test）：

   • 目的：检验两个或多个独立样本的分类变量分布是否存在差异。
   • 应用场景：当你想要比较不同样本或不同群体在某个分类变量上的分布是否一致时使用。例如，比较不同地区人群的吸烟率是否有显著差异。
   • 常用方法：卡方同质性检验（Chi-squared test for homogeneity）是常用的同质性检验方法。

3. 独立性检验（Independence test）：

   • 目的：检验两个分类变量之间是否存在关联或依赖关系。
   • 应用场景：当你想要分析两个分类变量之间是否存在某种联系时使用。例如，检验性别（男性/女性）和职业选择（工程师/非工程师）之间是否存在关联。
   • 常用方法：卡方独立性检验（Chi-squared test for independence）是常用的独立性检验方法。

区别总结：

• 适合性检验关注的是实际观测值与理论模型或期望值之间的拟合程度。
• 同质性检验关注的是不同样本或群体在某个分类变量上的分布是否一致。
• 独立性检验关注的是两个分类变量之间是否存在关联。

在实际应用中，选择哪种检验方法取决于你的研究问题和数据类型。例如，如果你的数据是分类变量，并且你想要检验它们之间的关联，那么独立性检验是合适的；如果你想要检验实际观测值是否符合某个理论分布，那么适合性检验是正确的选择；如果你想要比较不同样本在某个分类变量上的分布，那么同质性检验是合适的。

Assumptions 使用的前提 (large dataset)

• The variables must be categorical.
• Observations must be independent
  • Can assume from the task
• Cells in the contingency table are mutually exclusive.
  • Fits
• The expected value of cells should be 5 or greater in at least 80% of cells.

test of goodness-of-fit

例子： Is there a difference between the season preferences?
H0: There is no difference between the observed and expected season preferences
H1: There is a difference between the observed and expected season preferences

chisq.test(Poll_seasons, correct = FALSE, p = rep(1/4, 4))

test for homogeneity(需要判断两个分类变量是否是一样的或者不一样的)

Question: Is there a difference between the distribution of allergic reactions in the different
seasons?
H0: The distribution of allergic reactions is the same for the people who preferred different seasons
H1: The distribution of allergic reactions is not the same for the people who preferred different
seasons

问：不同季节过敏反应的分布有区别吗？H0：喜欢不同季节的人过敏反应分布相同 H1：喜欢不同季节的人过敏反应分布不一样

test of independency

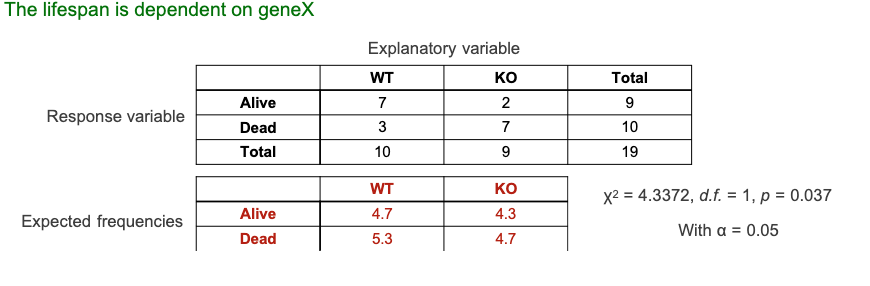
Question: We need to analyse the survival data of a geneX knockout mice at 1 year. Does geneX
affect lifespan of mice?
H0: The survival of mice is independent on geneX
H1: The survival of mice is dependent on geneX

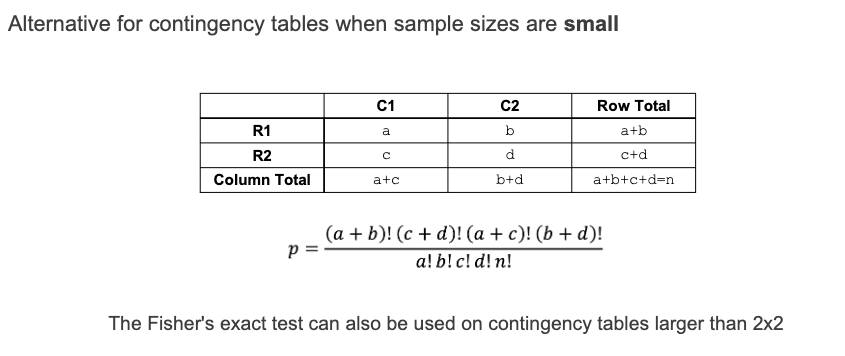
Fisher's exact test (在卡方检验不适合的时候就可以用)

当样本量很小的时候就可以用这个

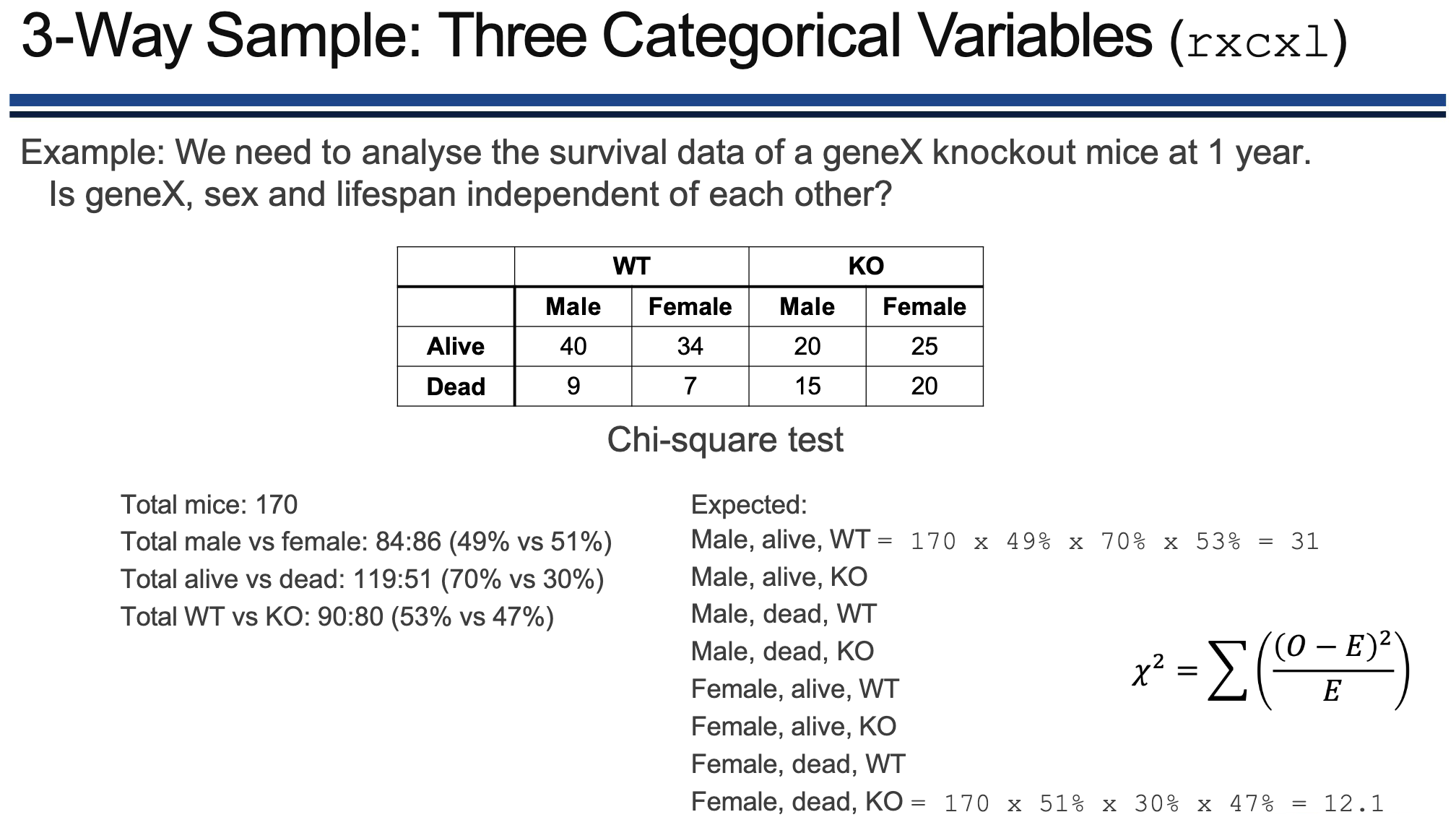
3-way ANNOVA

Kruskal-Wallis H test

Kruskal-Wallis H test（也称为一元方差分析的非参数替代方法）用于比较三个或更多个独立样本的中位数是否存在显著差异。当数据不满足ANOVA的正态分布假设时，Kruskal-Wallis检验是一个有用的非参数选择。

以下是使用R语言执行Kruskal-Wallis检验的步骤：

1. 确定假设:

   • 零假设 (H0): 所有组的中位数相同。
   • 备择假设 (H1): 至少有一个组的中位数与其他组不同。

2. 准备数据:

   • 确保数据是分成三个或更多组的独立样本。

3. 使用R执行Kruskal-Wallis检验:

   • 在R中，使用kruskal.test()函数来进行Kruskal-Wallis检验。

假设你有一个向量group表示样本所属的组，以及一个向量value表示对应的观测值，以下是如何使用kruskal.test()函数的示例：

# 假设有以下数据
group <- factor(c("A", "A", "B", "B", "C", "C"))
value <- c(10, 12, 15, 18, 20, 22)

# 执行Kruskal-Wallis检验
kruskal_result <- kruskal.test(value ~ group)

# 打印结果
print(kruskal_result)

在这个示例中，group是一个因子类型变量，用于指示每个观测值所属的组，而value是对应的数值型数据。kruskal.test(value ~ group)函数将执行检验，并返回一个包含检验统计量、自由度、P值等信息的对象。

结果解释:

• 如果P值小于常用的显著性水平（例如0.05），则拒绝零假设，认为至少有两个组之间存在显著差异。
• 如果P值大于显著性水平，则不能拒绝零假设，即没有足够证据表明组间中位数存在差异。

Kruskal-Wallis检验的结果只能告诉你至少有两个组之间存在差异，但它不会告诉你具体哪些组之间存在差异。如果检验结果显著，通常需要进一步的事后比较（如Mann-Whitney U检验）来确定具体哪些组之间存在差异。

Mann-Whitney U检验（也称为Wilcoxon秩和检验）是一种非参数检验，用于比较两个独立样本的中位数是否存在显著差异。当数据不满足正态分布假设或样本量较小时，此检验是一个合适的选择。

以下是使用R语言执行Mann-Whitney U检验的步骤：

1. 确定假设:

   • 零假设 (H0): 两个独立样本的中位数相同。
   • 备择假设 (H1): 两个独立样本的中位数不同。

2. 准备数据:

   • 确保你有两组独立的数据。

3. 使用R执行Mann-Whitney U检验:

   • 在R中，使用wilcox.test()函数来进行Mann-Whitney U检验。

假设你有两个向量sample1和sample2，分别代表两组独立样本的数据，以下是如何使用wilcox.test()函数的示例：

# 假设有以下两组独立样本数据
sample1 <- c(10, 12, 15, 18)
sample2 <- c(8, 14, 11, 17)

# 执行Mann-Whitney U检验
u_result <- wilcox.test(sample1, sample2)

# 打印结果
print(u_result)

在这个示例中，sample1和sample2是两组独立的数值型数据。wilcox.test(sample1, sample2)函数将执行Mann-Whitney U检验，并返回一个包含检验统计量、P值等信息的对象。

结果解释:

• 检验统计量: wilcox.test()返回的检验统计量是U值，它是根据秩次计算的。U值越小，表示两个样本之间的差异越大。
• P值: 如果P值小于常用的显著性水平（例如0.05），则拒绝零假设，认为两个独立样本的中位数存在显著差异。
• 如果P值大于显著性水平，则不能拒绝零假设，即没有足够证据表明两个样本的中位数存在差异。

请注意，wilcox.test()函数默认执行的是Wilcoxon秩和检验，它是Mann-Whitney U检验的一个变体，两者在解释上是相同的。此外，如果你的数据是配对样本，应该使用Wilcoxon符号秩检验（也称为Wilcoxon符号检验），这是通过在wilcox.test()函数中设置paired=TRUE参数来实现的。

# 假设有以下两组配对样本数据
paired_sample1 <- c(10, 12, 15, 18)
paired_sample2 <- c(8, 14, 11, 17)

# 执行Wilcoxon符号秩检验（配对样本）
signed_result <- wilcox.test(paired_sample1, paired_sample2, paired=TRUE)

# 打印结果
print(signed_result)

在配对样本的情况下，检验将考虑观测值之间的差异，而不是像独立样本那样分别对两组数据进行秩次排序。

CrossTable函数

P.S. 如何快速提取出列联表（甚至直接计算出chi-sq，但是直接计算有点不保险，最好还是提取出来再说）

library(gmodels)
head(mydata)
cross_table <- CrossTable(mydata$x, mydata$y) #应该要设置chisq=flase
chisq_result<- chisq.test(cross_table$t)

原始画表格

new_genotype <- data.frame(
  WT = c(nrow(subset(genotype, sex == "female" & genotype == "WT")),
         nrow(subset(genotype, sex == "male" & genotype == "WT"))),
  het = c(nrow(subset(genotype, sex == "female" & genotype == "het")),
          nrow(subset(genotype, sex == "male" & genotype == "het"))),
  mut = c(nrow(subset(genotype, sex == "female" & genotype == "mut")),
          nrow(subset(genotype, sex == "male" & genotype == "mut"))),
  row.names = c("female", "male")
)
···