ANNOVA test （one-way test and two-way test and bootstrapping）

对于ANNOVA的理解

什么情况下可以使用annova：

1. More than 2 populations
   对于多种不同药物对于某种疾病的效果的研究；比较不同国家指标的研究
2. More than 1 predictive variable (factor)
   锻炼和饮食对于健康的影响； effect of genetic background and drugs on stress levels
3. 如果是多way test
   2-way test: 2 factors, 比如effect of age and sex on salary

One-way annova

Null hypothesis: means of different <> groups are the same (老师标准写法)
或者说
Null hypothesis: There is no effects of class attendance or previous grades on course performance
Alternative hypothesis: means of different <> groups are not the same

核心思想：组内差异对比组间差异，如果这两者差异大就说明组内之间确实有差异；否则可以认为没有什么组间差异

统计前假设条件：

1. Independent random sampling
   We believe that this is true given the description of the experiment itself
2. normality of residuals (distance from group mean)

model <- aov(grade ~ attendance * previous_grades) # 这个地方，老师似乎认为没有理由能不使用interaction
hist((resid(model), main = "residuals")# 选一个，方法一
shapiro.test(resid(model)) #方法二

3. Equality of variances
   通过作图，“residuals vs fitted” plot进行查看

plot(model,1)

好的情况：

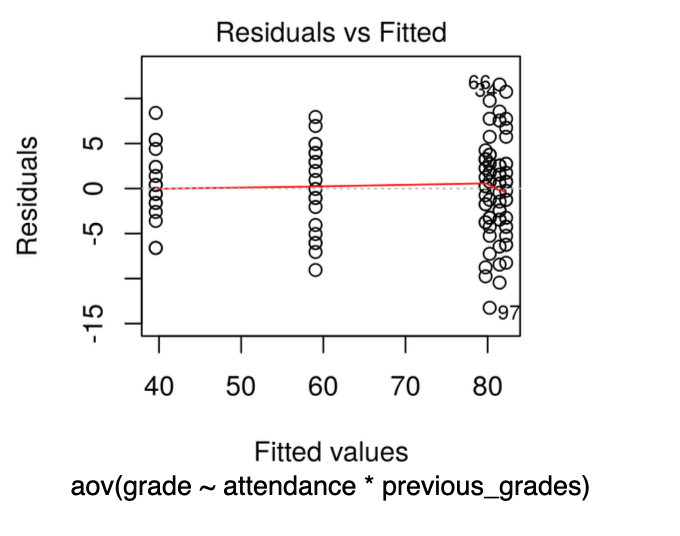
接下来查看统计量

summary(model)

实例结果：
Df Sum Sq Mean Sq F value Pr(>F)
Treatment 2 4.46 2.228 1.064 0.353
Measurement 1 2.05 2.049 0.979 0.328
Residuals 47 98.39 2.093

进行完ANNOVA 测试后，如果还想要知道具体是哪一组不同于另外几组，可以采用post-hoc tests。比如Tukey's HSD test

TukeyHSD(model)

如果想要探索，也可以思考两个factor之间是否有interaction， hypotheses变化：
• H0: There is no interaction between class attendance and previous grades
• HA: There is an interaction between class attendance and previous grades