最小生成树MST-07

概念
Kruskal算法（克鲁斯卡尔算法）
Prim算法（普里姆算法）
比较
MST应用场景
MST与最短距离
MST与 TSP

参考链接
https://cloud.tencent.com/developer/article/1480529

概念

最小生成树MST
应该叫最小总间距树 Mininum Spanning Tree

最小生成树（MST，Minimum Spanning Tree）是图论中的经典问题。让我详细为你讲解MST的概念和两种经典算法。
什么是最小生成树？
最小生成树是连通加权无向图中一棵权重和最小的生成树。它具有以下特点：

包含图中所有顶点
是一棵树（n个顶点，n-1条边，无环）
所有边的权重和最小

Kruskal算法（克鲁斯卡尔算法）

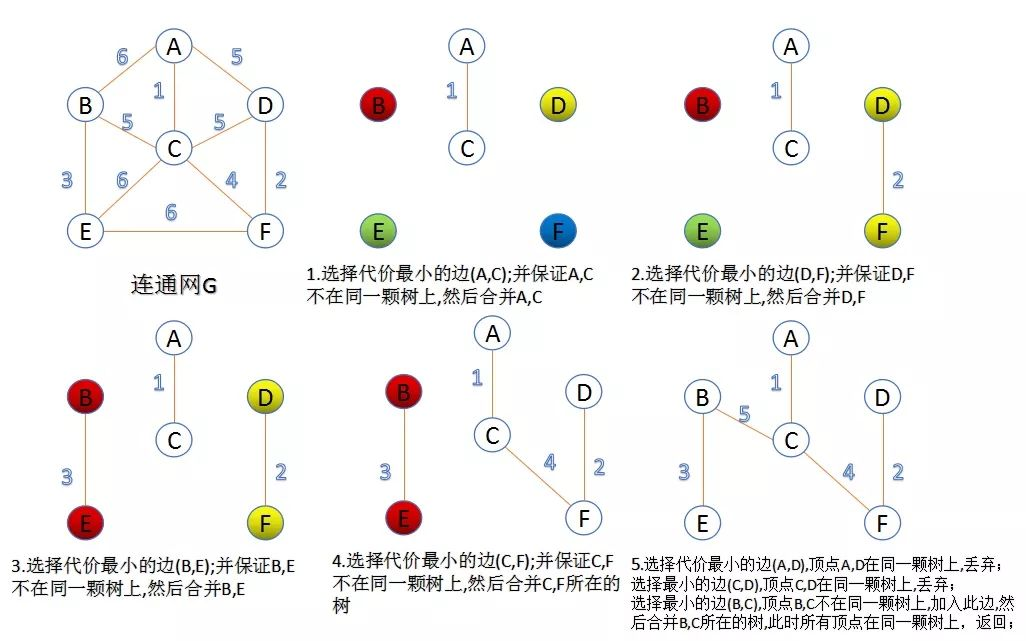
思想：贪心策略，按边权从小到大排序，依次加入不形成环的边。
步骤：
将所有边按权重从小到大排序
初始化并查集，每个顶点为一个独立的集合
遍历排序后的边，如果边连接的两个顶点不在同一集合中，则加入MST
重复直到MST包含n-1条边

class UnionFind:
    """并查集数据结构"""
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [0] * n
    
    def find(self, x):
        """查找根节点（路径压缩优化）"""
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    
    def union(self, x, y):
        """合并两个集合（按秩合并优化）"""
        px, py = self.find(x), self.find(y)
        if px == py:
            return False
        if self.rank[px] < self.rank[py]:
            px, py = py, px
        self.parent[py] = px
        if self.rank[px] == self.rank[py]:
            self.rank[px] += 1
        return True

def kruskal_mst(n, edges):
    """
    Kruskal算法求最小生成树
    
    参数:
    n: 顶点数量
    edges: 边的列表，每条边格式为 (权重, 顶点1, 顶点2)
    
    返回:
    (mst_edges, total_weight): MST的边列表和总权重
    """
    # 按权重排序所有边
    edges.sort()
    
    uf = UnionFind(n)
    mst_edges = []
    total_weight = 0
    
    for weight, u, v in edges:
        # 如果u和v不在同一连通分量中，加入这条边
        if uf.union(u, v):
            mst_edges.append((u, v, weight))
            total_weight += weight
            # MST包含n-1条边时完成
            if len(mst_edges) == n - 1:
                break
    
    return mst_edges, total_weight

# 示例使用
if __name__ == "__main__":
    # 图的表示：顶点编号0到5，边格式为(权重, 起点, 终点)
    n = 6
    edges = [
        (4, 0, 1), (6, 0, 2), (6, 0, 3),
        (2, 1, 2), (5, 1, 4),
        (1, 2, 3), (5, 2, 4), (3, 2, 5),
        (4, 3, 5),
        (6, 4, 5)
    ]
    
    mst_edges, total_weight = kruskal_mst(n, edges)
    
    print("Kruskal算法结果：")
    print("MST边：", mst_edges)
    print("总权重：", total_weight)
    
    # 可视化MST
    print("\nMST边详情：")
    for u, v, w in mst_edges:
        print(f"顶点 {u} -- 顶点 {v}：权重 {w}")

总结：
克鲁斯卡尔算法的核心思想：贪心。
总是优先选择权重最小的边。
然后检查这条边是否会形成一个环。
如果不会，就把它加到最小生成树中。
重复这个过程，直到所有顶点都连通起来。

这个过程就像建造一座桥，手头有各种长度的木板（边），你总是优先使用最短的木板（最小权重边），但要确保每使用一块木板，都没有形成一个封闭的回路。

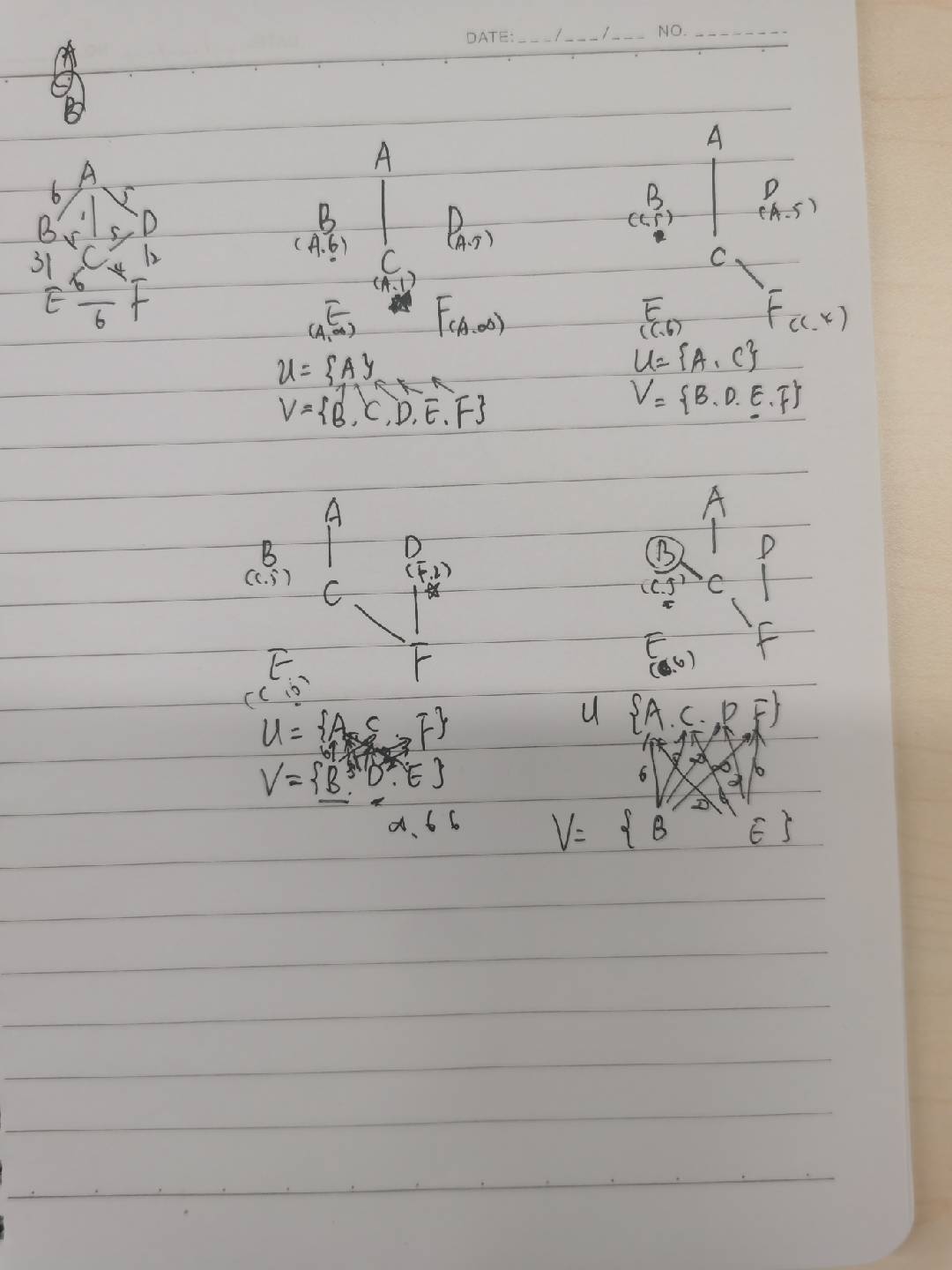
第一次读上面的代码还是很绕的，

初始的 self.parent = [0,1,2,3,4,5]
self.parent 这个长度是6的列表来描述父子关系只要这个parent列表确定了就能将树画出来

find(x)的逻辑一层一层往上查找直到 self.parent[x] == x 满足这个条件的及时根节点因为初始的个点就是单独的 6课树

合并的逻辑
小树合到大树，大鱼吃小鱼如何大树合到小树那大树要查找父节点都需要边长复杂度更大

按秩合并是 union 操作的一种优化策略，它和路径压缩是并查集最常用的两种优化，通常一起使用。它的主要目的是保持并查集形成的树结构尽可能地平衡和扁平，防止树变得过高，从而保证 find 操作的效率。
为什么需要按秩合并？
在没有按秩合并的情况下，union 操作通常是随机地将一棵树的根节点指向另一棵树的根节点。这可能导致一种极端情况：

树 A 只有 1 个节点。
树 B 有 100 个节点，并且形成了一条长链。
如果我们将 B 的根节点指向 A 的根节点，那么这棵树就会变得非常不平衡，find 操作的效率会大大降低。

按秩合并就是为了避免这种情况。

按秩合并确保了并查集形成的树结构总是保持平衡，结合路径压缩，它们能将并查集的平均时间复杂度降至接近常量级（技术上是 O(α(n))，其中 α(n) 是反阿克曼函数，增长速度极其缓慢，对于实际问题可以认为是常量）。

这两项优化策略的结合，使得并查集成为处理连接关系和连通性问题（如克鲁斯卡尔算法）时，性能非常优越的数据结构。

Prim算法（普里姆算法）

思想：从某个顶点开始，逐步扩展MST，每次选择连接MST和非MST顶点的最小权重边。
步骤：

选择起始顶点加入MST
维护一个优先队列，存储连接MST和非MST顶点的边
每次取出最小权重边，如果终点不在MST中，则加入MST
更新优先队列，加入新顶点的所有邻接边

import heapq
from collections import defaultdict

def prim_mst(n, edges, start=0):
    """
    Prim算法求最小生成树
    
    参数:
    n: 顶点数量
    edges: 边的列表，每条边格式为 (权重, 顶点1, 顶点2)
    start: 起始顶点（默认为0）
    
    返回:
    (mst_edges, total_weight): MST的边列表和总权重
    """
    # 构建邻接表
    graph = defaultdict(list)
    for weight, u, v in edges:
        graph[u].append((weight, v))
        graph[v].append((weight, u))
    
    # 初始化
    visited = set()
    mst_edges = []
    total_weight = 0
    min_heap = []  # 优先队列：(权重, 起点, 终点)
    
    # 从start顶点开始
    visited.add(start)
    
    # 将start的所有邻接边加入优先队列
    for weight, neighbor in graph[start]:
        heapq.heappush(min_heap, (weight, start, neighbor))
    
    while min_heap and len(mst_edges) < n - 1:
        weight, u, v = heapq.heappop(min_heap)
        
        # 如果终点已经在MST中，跳过这条边
        if v in visited:
            continue
        
        # 将边加入MST
        visited.add(v)
        mst_edges.append((u, v, weight))
        total_weight += weight
        
        # 将新顶点v的所有邻接边加入优先队列
        for next_weight, neighbor in graph[v]:
            if neighbor not in visited:
                heapq.heappush(min_heap, (next_weight, v, neighbor))
    
    return mst_edges, total_weight

def prim_mst_matrix(adj_matrix, start=0):
    """
    Prim算法的邻接矩阵实现（经典版本）
    
    参数:
    adj_matrix: 邻接矩阵，adj_matrix[i][j]表示顶点i到j的权重，0表示无边
    start: 起始顶点
    
    返回:
    (mst_edges, total_weight): MST的边列表和总权重
    """
    n = len(adj_matrix)
    visited = [False] * n
    min_edge = [float('inf')] * n  # 到MST的最小边权重
    parent = [-1] * n  # 记录父节点
    
    # 起始顶点
    min_edge[start] = 0
    mst_edges = []
    total_weight = 0
    
    for _ in range(n):
        # 找到未访问顶点中min_edge最小的
        u = -1
        for v in range(n):
            if not visited[v] and (u == -1 or min_edge[v] < min_edge[u]):
                u = v
        
        visited[u] = True
        
        # 如果不是起始顶点，添加边到MST
        if parent[u] != -1:
            mst_edges.append((parent[u], u, adj_matrix[parent[u]][u]))
            total_weight += adj_matrix[parent[u]][u]
        
        # 更新相邻顶点的最小边权重
        for v in range(n):
            if not visited[v] and adj_matrix[u][v] > 0:
                if adj_matrix[u][v] < min_edge[v]:
                    min_edge[v] = adj_matrix[u][v]
                    parent[v] = u
    
    return mst_edges, total_weight

# 示例使用
if __name__ == "__main__":
    # 使用边表示的图
    n = 6
    edges = [
        (4, 0, 1), (6, 0, 2), (6, 0, 3),
        (2, 1, 2), (5, 1, 4),
        (1, 2, 3), (5, 2, 4), (3, 2, 5),
        (4, 3, 5),
        (6, 4, 5)
    ]
    
    mst_edges, total_weight = prim_mst(n, edges)
    
    print("Prim算法结果（邻接表版本）：")
    print("MST边：", mst_edges)
    print("总权重：", total_weight)
    
    # 邻接矩阵版本
    adj_matrix = [
        [0, 4, 6, 6, 0, 0],
        [4, 0, 2, 0, 5, 0],
        [6, 2, 0, 1, 5, 3],
        [6, 0, 1, 0, 0, 4],
        [0, 5, 5, 0, 0, 6],
        [0, 0, 3, 4, 6, 0]
    ]
    
    mst_edges2, total_weight2 = prim_mst_matrix(adj_matrix)
    
    print("\nPrim算法结果（邻接矩阵版本）：")
    print("MST边：", mst_edges2)
    print("总权重：", total_weight2)
    
    # 可视化MST
    print("\nMST边详情：")
    for u, v, w in mst_edges:
        print(f"顶点 {u} -- 顶点 {v}：权重 {w}")

比较

Kruskal算法

时间复杂度：O(E log E)，主要是边排序的时间
空间复杂度：O(V)，并查集的空间
适用场景：稀疏图（边数相对较少）

Prim算法

时间复杂度：
使用优先队列：O(E log V)
使用邻接矩阵：O(V²)

空间复杂度：O(V + E)
适用场景：稠密图（边数较多）

算法选择建议

图较稀疏（E接近V）：选择Kruskal算法
图较稠密（E接近V²）：选择Prim算法
已有邻接矩阵：Prim算法更方便
需要在线算法：Prim算法可以逐步构建

核心思想对比

Kruskal：边的角度，全局最优选择
Prim：顶点的角度，局部扩展策略

MST应用场景

MST的主要应用场景

网络基础设施设计

电力网格：以最小成本连接所有发电站和变电站
通信网络：设计光纤骨干网，最小化铺设成本
供水系统：连接水源到所有用户的管道网络
交通网络：规划公路、铁路的基础连接

聚类分析

数据挖掘：基于特征相似性对数据进行分组
图像分割：将相似像素区域归为一类
社交网络：发现社区结构和用户群体
基因分析：基于序列相似性对基因进行分类

近似算法基础

TSP问题：提供2-近似解的理论保证
斯坦纳树问题：网络设计的扩展问题
设施选址：优化服务设施的布局

MST与最短距离

核心区别：

优化目标不同：

MST：最小化所有连接的总成本
最短路径：最小化特定两点间的距离

解的结构不同：

MST：树结构（n-1条边，无环）
最短路径：路径序列

应用场景不同：

MST：网络设计、基础设施建设
最短路径：导航、路由、物流

MST对最短路径的帮助：

有限帮助：MST不能直接解决点到点最短路径
预处理作用：可以作为某些最短路径算法的预处理步骤
近似解：在某些特殊图中，MST路径可能接近最短路径

MST与 TSP

TSP 是旅行商问题兜一圈回到出发点访问所有的点总路径最短

TSP最优解 ≥ MST权重
因为TSP路径去掉一条边就是生成树
算法选择建议
选择MST算法的场景：

✅ 需要连接所有节点且总成本最小
✅ 设计基础网络拓扑
✅ 进行数据聚类分析
✅ 构造复杂问题的近似解

选择最短路径算法的场景：
✅ 需要找到两点间最快/最短路径
✅ 网络路由和导航
✅ 物流配送路径优化
✅ 实时路径查询

MST是连接性问题的最优解，而最短路径是可达性问题的最优解。虽然它们解决的是不同类型的问题，但MST在很多复杂问题（如TSP）中扮演着重要的理论和实践角色。理解这些算法的适用场景和相互关系，有助于在实际问题中选择合适的解决方案。

posted @ 2025-09-20 16:45 jack-chen666 阅读(25) 评论(0) 收藏举报

刷新页面返回顶部

红豆生南国是很遥远的事情

种豆南山下 github

最小生成树MST-07

概念

Kruskal算法（克鲁斯卡尔算法）

Prim算法（普里姆算法）

比较

MST应用场景

MST与最短距离

MST与 TSP

公告

红豆生南国 是很遥远的事情

种豆南山下 github

最小生成树MST-07

概念

Kruskal算法（克鲁斯卡尔算法）

Prim算法（普里姆算法）

比较

MST应用场景

MST与 最短距离

MST与 TSP

公告

红豆生南国是很遥远的事情

MST与最短距离