图像生成-FUDUKI解读-Preliminary: Discrete Flow Matching -15
参考
https://arxiv.org/pdf/2505.20147


来深入解读FUDOKI论文的第二部分 Preliminary: Discrete Flow Matching。这部分是理解整篇论文的基石,它将我们之前讨论的连续流(CNF)思想,巧妙地“翻译”到了离散数据的世界中。
核心转变:从连续空间到离散空间
这是理解DFM的第一步,也是最重要的一步。
CNF的世界:我们处理的是连续数据,比如图像。一张图片可以看作是高维实数空间 \(ℝ^D\) 中的一个点,每个像素值都可以是0到255之间的任意浮点数。
DFM的世界:我们处理的是离散数据,比如文本或者被编码后的图像。数据 \(x\) 属于离散空间 \(S = T^D\)
\(T\) 是一个有限的“词汇表”(Token Vocabulary),比如 \({1, 2, ..., K}\)。
\(D\) 是序列的长度。
一个数据样本 \(x = (x¹, x², ..., x^D)\) 就是一个由D个“词”组成的句子或序列。
为什么这个转变很重要?
因为语言是天生离散的。而且,现在很多强大的多模态模型(如ViT, GPT)都倾向于将图像、声音等连续信号“Tokenize”(离散化),转换成统一的Token序列来处理。FUDOKI正是建立在这个统一的离散表示之上。
离散世界中的“概率路径” \(p_t(x)\)
在CNF中,我们用一个移动并缩放的“高斯云”来定义路径。
在离散世界里,这个方法行不通了。因此,论文提出了一种新的、同样非常巧妙的路径定义方法
DFM的概率路径\(p_t(x)\)同样是由无数条简单的条件路径 \(p_t(x|x₁)\) 加权平均而成的。关键在于\(p_t(x|x₁)\)是如何定义的。
条件路径 \(p_t(x|x₁)\):从“高斯云”到“概率混合”
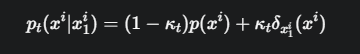
这是DFM的核心路径公式,我们来解读它:
\(x₁^i\): 目标序列中第 i 个位置的正确Token。
\(p(x^i)\): 一个基础分布,代表“随机噪声”。在离散世界里,这通常是一个在所有K个Token上的均匀分布(即每个Token被选中的概率都是\(1/K\)),或者是一个指向特殊\([MASK]\) Token的分布。
\(δ_{x_1^i}(x^i)\): 这是一个点质量分布(Kronecker delta函数)。你可以把它理解成一个“绝对确定”的分布,它的所有概率都100%集中在正确的\(Token x₁^i\) 上
\(κ_t (kappa_t)\): 这是一个从0到1变化的“混合旋钮”或“调度器”。
径的演化过程非常直观:
在 \(t=0\) 时 \((κ₀ = 0)\): \(p₀(x^i|x₁^i) = p(x^i\))。此时,序列中的每个位置都是一个完全随机的Token(噪声)。
在 \(t=1\) 时 \((κ₁ = 1)\): \(p₁(x^i|x₁^i) = δ_{x₁^i}(x^i)\)。此时,序列中的每个位置都确定无疑是那个正确的数据Token。
在 \(0 < t < 1\) 时: 这是一个概率混合。在任何一个位置,它有 \(κ_t\) 的概率变成正确的Token,有 \((1-κ_t)\) 的概率保持为一个随机的Token。
通过调节 \(κ_t\),我们就构建了一条从“完全随机”平滑过渡到“完全正确”的离散概率路径。

离散世界中的“速度” \(u_t\)
在CNF中,我们用ODE(常微分方程)来描述粒子的“移动速度”。
在离散世界里,粒子不是“移动”,而是从一个状态“跳跃”到另一个状态。
论文引入了连续时间马尔可夫链 (Continuous-Time Markov Chain, CTMC) 来描述这个过程。
CTMC: 这是描述一个系统在连续时间里,在不同离散状态间随机“跳跃”的数学工具。
概率速度 \(u_t(x', z)\): 在DFM中,“速度”的含义变成了从Token \(z\) 跳跃到 Token \(x'\) 的瞬时速率(rate)。
它是一个\(K x K\)的速率矩阵,描述了词汇表中任意两个Token之间相互转换的快慢。
离散连续性方程 (Discrete Continuity Equation)
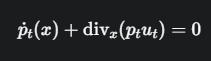
这个公式在形式上和我们之前看到的CNF(Continuous Normalization Flow)版本几乎一样,但内部的含义已经变成了离散版本:
\(ṗ_t(x)\): 序列 \(x\) 的概率随时间的变化率。
\(div_x(p_t u_t)\): 离散散度。截图给出了它的精确定义:
$$div_x(p_t u_t) = Σ (从x出发的总流出量) - Σ (流向x的总流入量)$$
这再次印证了那个守恒定律:一个特定序列 x 的概率会增加,唯一的原因是其他序列“跳跃”成 x 的总速率,超过了 x “跳跃”成其他序列的总速率。概率不会凭空产生或消失,只会在不同的离散状态之间“流动”。
DFM巧妙地将CNF的整套思想,通过替换核心组件(高斯路径 -> 混合路径,ODE -> CTMC),成功地应用到了处理语言和其他离散数据的领域,为FUDOKI这样统一的多模态模型铺平了道路。
CTMC:连续时间马尔可夫链 (Continuous-Time Markov Chain, CTMC)
详细解读 离散空间的连续性方程
高维离散空间里发生的动态过程

想象一下,我们正在一个有很多很多独立房间(比如成千上万个)的大房子里举办一场派对。
离散状态 \(x\):代表一间特定的房间。比如,“房间A”、“房间B”、“房间C”..
概率 \(p_t(x)\):代表在 \(t\) 时刻,待在房间 \(x\) 里的人数(或者说人数占总人数的比例)。
速度 \(u_t(y, x)\):代表从房间 \(x\) 走到 房间 \(y\) 的意愿强度或速率。这个值越大,说明 \(x\) 房间的人越想去 \(y\) 房间。
流量/通量 (Flux):\(p_t(x) * u_t(y, x)\),代表实际正在从房间 \(x\) 走向房间 \(y\) 的人流量。
如果房间 \(x\) 有10个人,他们想去房间 \(y\) 的意愿是0.5,那么人流量就是 \(10 * 0.5 = 5\) 人/秒。
现在,我们把焦点放在一间特定的房间,就叫它“客厅”(状态 x)吧。我们来分析“客厅”里的人数是如何变化的。
公式:\(ṗ_t(x) + div_x(p_t u_t) = 0\)
这个公式由两部分组成,我们用“派对”的语言来翻译它们:
第一部分:\(ṗ_t(x)\) —— 客厅人数的变化 --注意上面的一点 代表的是导数
\(ṗ_t(x)\) 是 \(p_t(x)\) 对时间的导数。
比喻翻译:它衡量的就是“客厅”里人数的变化速度。
如果 \(ṗ_t(x)\) 是正数,说明此刻客厅里的人正在变多。
如果 \(ṗ_t(x)\) 是负数,说明此刻客厅里的人正在变少。
如果 \(ṗ_t(x)\) 是0,说明人数保持不变。
第二部分:\(div_x(p_t u_t)\) —— 客厅的“净流出人数”
\(div\) 是散度(Divergence),这是一个衡量“净流出”的数学工具。
您截图里对它的定义非常关键和直观:
比喻翻译:
总流出量:从“客厅”出发,走向所有其他房间的总人流量。
总流入量:从所有其他房间,走进“客厅”的总人流量。
\(div_x\) 就等于 (离开客厅的总人数) - (进入客厅的总人数)。它衡量的就是“客厅”这个地方,在某一瞬间的净流出人数。
“啊哈!”时刻:把公式连起来
现在我们把公式 \(ṗ_t(x) + div_x(p_t u_t) = 0\) 重新排列一下,变成:
\(ṗ_t(x) = - div_x(p_t u_t)\)
现在,我们把“比喻翻译”代入进去:
(客厅人数的变化速度) = - (客厅的净流出人数)
(客厅人数的变化速度) = - ( (离开的总人数) - (进入的总人数) )
(客厅人数的变化速度) = (进入的总人数) - (离开的总人数)
它说的就是一句大白话:客厅里人数的变化,就等于进来了多少人,减去了离开了多少人。
这个离散连续性方程,尽管名字听起来很吓人,但它本质上只是一个“守恒定律”。
在我们的AI模型里,它保证了概率的守恒。
一个特定的词序列(一个“房间”)的概率 \(p_t(x)\) 会发生改变,不是因为它会凭空产生或消失,而是因为其他的序列通过“跳跃”(人流走动)变成了它,或者它“跳跃”成了别的序列。
这个方程建立了“状态”(概率 \(p_t\))和“行为”(速度 \(u_t\))之间的铁律
是整个Flow Matching理论能够从连续世界延伸到离散世界的数学桥梁。希望这个“派对比喻”能帮助您彻底理解它!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号