图像生成-flow matching 条件化-13

参考

https://g.co/gemini/share/c0f7881543f7
https://zhuanlan.zhihu.com/p/685921518

这部分内容是 Flow Matching 框架下的具体“工程实践”。我们已经知道了“条件化”是解决问题的关键，现在的问题是：具体应该选择什么样的条件路径 \(p_t(x|x₁)\) 和条件向量场 \(u_t(x|x₁)\) 呢？

两种主流的设计思路：一种是借鉴经典的扩散模型（Diffusion），另一种是采用更直接的最优传输（Optimal Transport, OT）。

设计的灵活性

Flow Map的设计（即μ_t和σ_t函数的设计）是非常灵活的。我们可以根据不同的应用场景和需求，选择不同的函数。

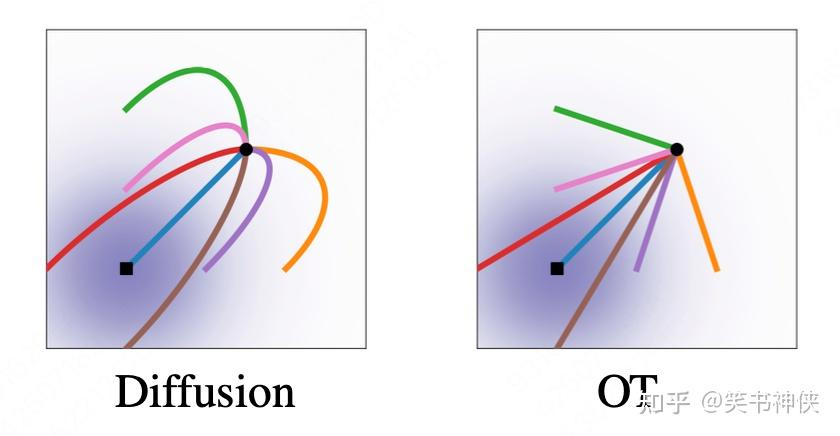
非常形象的方式展示了两种设计思路产生的路径差异：
Diffusion（左图）：从噪声点（黑色方块）到数据点（所有曲线的交汇点）的路径是弯曲的（curved）。
OT（右图）：路径是笔直的（straight）。
这两种路径形状的差异，是这两种方法本质区别的最直观体现。

思路一：扩散条件向量场 (Diffusion conditional Vector Fields)

这个思路是“站在巨人的肩膀上”。我们直接借鉴经典扩散模型（如DDPM）中使用的加噪过程，来反向定义我们的条件路径。这通常会产生非线性的、弯曲的路径。

两种源于扩散模型的思路：

Variance Exploding (VE) - 方差爆炸式

来自一类早期扩散模型，它们在加噪（前向）过程中，信号的强度不变，但噪声的方差会随时间急剧增大（爆炸）。
在CFM（continuous flow matching）中的应用:我们会设计一个\(μ_t\)和\(σ_t\)，来模拟这个过程的逆过程。简单来说，它的路径不是笔直地飞向终点，而是会走一条特定的曲线。这条曲线的“弯曲度”由这些VE模型的特定参数决定。

Variance Preserving (VP) - 方差保持式
这是最著名的DDPM模型所采用的策略。它在加噪过程中，通过同时缩减信号和增加噪声，使得信号和噪声的总方差大致保持不变（为1）。
在CFM（continuous flow matching）中的应用：我们直接把DDPM的加噪公式拿过来，把时间\(t\)换成\(1-t\)来逆转它，从而定义我们的条件路径参数\(μ_t\)和\(σ_t\)。
\(μ_t = α_{1-t} * x₁\)
\(σ_t = √(1 - α_{1-t}²)\)
路径特点：由于\(α\)本身是\(β\)的累乘，是一个非线性的量，所以均值\(μ_t\)的变化不是线性的，它导致了路径也是弯曲的。
小结：Diffusion思路的好处是理论成熟，可以直接借用已有模型的参数。但缺点是路径较为复杂，可能是“绕路”的。

最优传输条件向量场 (Optimal Transport conditional Vector Fields)

这个思路更加直接和“功利”。它抛弃了复杂的扩散动力学，追求的是从起点分布到终点分布“最经济”、“最直接”的路径。在很多情况下，最经济的路径就是直线。
这对应了我们之前一直作为范例的、最简单的路径设计：

均值 μ_t 的设计：
\(μ_t(x) = t * x₁\)
含义：概率云的中心，从t=0的原点，线性地、笔直地移动到t=1的目标x₁。

标准差 σ_t 的设计：
\(σ_t(x) = 1 - (1 - σ_min)t\)
含义：概率云的半径，从\(t=0\)的1，线性地、均匀地收缩到\(t=1\)的\(σ_min\) (一个接近0的数)。
\(σ_min\)是接近0的一个数 但不能等于0 等于0是不可能的，取倒数会变成无穷大

路径的最终形态与速度场：

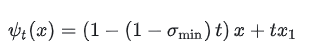
Flow Map (路径)：这个公式表明，任何一个初始噪声点，其运动轨迹都是一条直线。

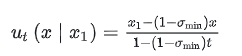
条件向量场，这是通过Theorem 3计算出的、能驱动上述直线运动的、精确的速度场公式。

最优传输路径轨迹为直线，而扩散路径轨迹为曲线。
因此可以得到更快的训练速度和生成速度，以及更好的性能表现。

这是整个对比的最终结论，也是Flow Matching方法的核心优势之一。
路径更短：直线是两点间最短的路径。模型需要学习的变换总长度更短，收敛可能更快。
目标更简单：学习一个驱动直线运动的速度场，通常比学习一个驱动曲线运动的速度场要更容易。这个学习目标对于神经网络来说更“友好”。
稳定性：直线的路径和线性变化的方差，使得整个训练过程更加稳定可控。

总结：

虽然我们可以从经典的扩散模型中借鉴思路来构建“弯曲”的条件路径，但在Flow Matching的框架下，采用最优传输思想构建的“笔直”路径，往往是更简单、更高效、也更强大的选择。这使得Flow Matching不仅在理论上优雅，在实践中也表现出色。