图像生成-连续性方程-09

目录

• 参考
• 回顾与动机：CNF的困境
• 连续性方程（The Law of Conservation）
• 从物理到概率：概率的守恒

参考

https://zhuanlan.zhihu.com/p/685921518

Flow Matching 是在 CNF(连续归一化流) 基础上发展而来的一种更高效、更直接的训练方法，而理解图中的连续性方程（Continuity Equation）正是理解Flow Matching的关键所在。这部分内容确实融合了物理和数学，比较抽象

回顾与动机：CNF的困境

回忆一下刚刚讨论的连续归一化流（CNF）。CNF非常强大，但它的训练过程很“绕”：
为了计算损失（负对数似然），我们需要求解一个复杂的ODE（常微分方程），并计算一个难以处理的“迹的积分”。

v是一个复杂的神经网络，我们无法得到解析解，只能使用数值方法来近似求解。最简单的方法就是欧拉法。

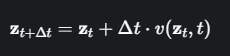
累加项变成了一个积分项，并且被求和的项从行列式（determinant）变成了迹（trace）。

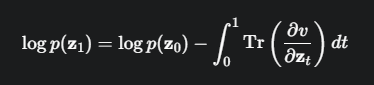
这个过程计算量巨大，训练非常缓慢。
Flow Matching的出发点：我们能不能找到一种更直接的训练方法？我们能不能不绕那么大一个圈子，而是直接去学习那个能驱动概率流动的“速度场” \(v(x,t)\)？
答案是肯定的，连续性方程”就是实现这一点的理论基石。

连续性方程（The Law of Conservation）

自于流体力学，它描述了流体（比如水）的质量守恒定律。

用一个更生活化的比喻来理解它——广场上的人群。
\(ρ (rho)\): 人群的密度。某个地方 \(ρ\) 很高，说明那里人挤人。
\(v\): 人群的移动速度。一个向量，指向人群移动的方向
\(∂ρ/∂t\): 某个地点人群密度的变化率。如果是负数，说明这个地方的人在变少。
\(div(ρv)\): 人群的净流出率。div叫做散度，它衡量一个向量场从一个点“发散”出去的程度。
如果一个地方的 div 是正数，说明从这里走的人比来的人多（净流出）--（泉眼）。
如果 div 是负数，说明来的人比走的人多（净流入/汇聚）--（旋涡 黑洞）。

所以，这个物理公式的大白话版本就是：

\[（一个地方人群密度的变化）+（这个地方人群的净流出）= 0 \]

一个地方的人群密度之所以会变化，唯一的原因就是有人流进或流出。人不会凭空产生，也不会凭空消失。 这就是“守恒”。

从物理到概率：概率的守恒

现在，最精彩的一步来了。我们把“人群”换成“概率”。
人群的总数是守恒的。
概率的总和（积分为1）也是守恒的！
可以把描述人群流动的连续性方程，完美地类比到描述概率密度的流动上。

概率连续性方程：

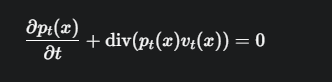
\(p_t(x)\): \(t\) 时刻 \(x\) 位置的概率密度（相当于人群密度 ρ）。
\(v_t(x)\): 驱动概率流动的向量场（相当于人群移动速度 v）。
\(∂p_t/∂t\): 概率密度的时间变化率。
\(div(p_t * v_t)\): 概率的净流出率。

这个公式揭示了一个深刻的真理：一个时间变化的概率密度路径 \(p_t(x)\) 和一个时间变化的向量场 \(v_t(x)\) 是一一对应的、被这个方程牢牢绑定的关系。