图像生成-概率密度函数的变量变换--06
参考
https://zhuanlan.zhihu.com/p/685921518

概率密度函数的变量变换
这个知识点叫做 ** 概率密度函数的变量变换(Change of Variable for Probability Density Function, PDF),主要用于当你对一个随机变量进行变换后,如何计算新变量的概率密度函数。**
随机变量 它有一个已知的概率密度函数。现在我们对它做了一个可逆函数变换:
它有一个已知的概率密度函数。现在我们对它做了一个可逆函数变换:
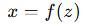
那么反过来我们也可以写成: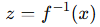
接下来我们希望知道:新的随机变量 𝑥 的概率密度函数 𝑝(𝑥) 是多少?
概率密度的直觉含义是“单位长度(或体积)上的概率”,当我们对变量做变换时,单位长度或体积也会发生缩放或扭曲,因此密度也会相应变化。
变量变换时,概率是不变的,即:
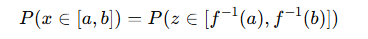
所以,概率密度需要乘上一个雅可比行列式(Jacobian determinant)来修正缩放的影响。
当 𝑧 是一维随机变量
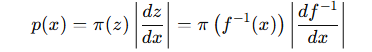
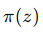 原始变量 𝑧 的密度函数。
原始变量 𝑧 的密度函数。
 表示新变量 𝑥 对应的旧变量 𝑧。
表示新变量 𝑥 对应的旧变量 𝑧。
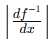 是缩放系数(Jacobian 的绝对值),表示密度如何随着变量的变化被拉伸或压缩。
是缩放系数(Jacobian 的绝对值),表示密度如何随着变量的变化被拉伸或压缩。
举例1:
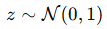 (标准正态分布)
(标准正态分布)
做变换: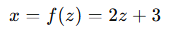
求 𝑥 的分布。
反函数为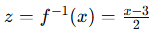
雅可比项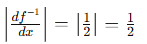 # 注意带有绝对值符号
# 注意带有绝对值符号
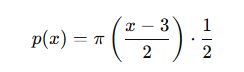 其中\(Π\)是标准的正态密度函数
其中\(Π\)是标准的正态密度函数
举例2:
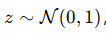 标准正态分布
标准正态分布
变换函数: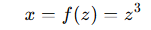
我们希望求出新的变量 𝑥 的概率密度函数 𝑝(𝑥)。
求反函数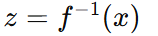
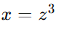
反函数为: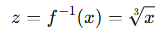
求导数+绝对值符号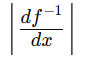
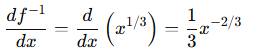
取绝对值: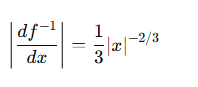
套用变量变换公式:

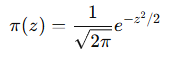
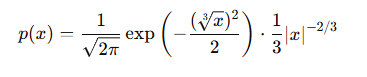
直觉解释:
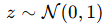 一个对称的分布
一个对称的分布
变换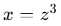 会把负数变得更负,正数变得更正,并压缩靠近零的区域,所以密度会变形
会把负数变得更负,正数变得更正,并压缩靠近零的区域,所以密度会变形
新的分布 𝑝(𝑥) 会是非对称的、非高斯的,且在 𝑥=0 处密度特别高
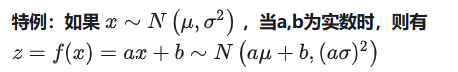


 浙公网安备 33010602011771号
浙公网安备 33010602011771号